 |
Математические модели расчета тарифных ставок
|
|
|
|
Тарифная ставка - это цена страхового риска и других расходов, адекватное денежное выражение обязательств страховщика по заключенному договору страхования.
Тарифная ставка, по которой заключается договор страхования, носит название брутто-ставки. Собственно нетто-ставка выражает цену страхового риска: пожара, наводнения, взрыва. Нагрузка покрывает расходы страховщика по организации и проведению страхового дела, включает отчисления в запасные фонды, содержит элементы прибыли.
При составлении страхового тарифа следует учитывать, что страховыми взносами необходимо покрывать не только страховые суммы и возмещения, но и расходы на содержание страховой компании.
Процесс разработки и обоснования страхового тарифа называется тарифной политикой, под которой понимается целенаправленная деятельность страховщика по установлению, уточнению и упорядочению страховых тарифов в интересах успешного и безубыточного развития страхования.
Рассмотрим методику расчета тарифных ставок для рисковых видов страхования, которая применима при имущественном страховании при следующих условиях:
1) Существует статистика либо какая-то другая информация по рассматриваемому виду страхования, что позволяет оценить следующие величины:
- вероятность наступления страхового случая по одному договору страхования,
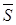- среднюю страховую сумму по одному договору страхования,
- среднее возмещение по одному договору страхования при наступлении страхового случая.
2) Предполагается, что не будет опустошительных событий, когда одно событие влечет за собой несколько страховых случаев.
3) Расчет тарифов проводится при заранее известном количестве договоров 
, которые предполагается заключить со страхователями.
|
|
|
При наличии статистики по рассматриваемому виду страхования за величины , , 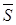принимаются оценки их значений:
; (1)
; (2)
; (3)
где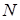 
- общее количество договоров, заключенных за некоторый период времени в прошлом; 
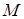- количество страховых случаев в 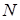договорах; 
- страховая сумма при заключении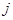 
- го договора, 
; 
- страховое возмещение при k - ом страховом случае,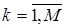 
.
При страховании по новым видам рисков при отсутствии фактических данных о результатах проведения страховых операций, т.е. статистики по величинам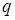 
, 
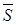и 
, эти величины могут оцениваться экспертным методом либо в качестве них могут использоваться значения показателей-аналогов. В этом случае должны быть представлены мнения экспертов либо пояснения по обоснованности выбора показателей-аналогов , 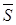и .
Отношение средней выплаты к средней страховой сумме (
) рекомендуется принимать не ниже:
0,3 - при страховании от несчастных случаев и болезней (в медицинском страховании);
0,4 - при страховании средств наземного транспорта;
0,5 - при страховании грузов и имущества (кроме средств транспорта);
0,6 - при страховании средств воздушного и водного транспорта;
0,7 - при страховании ответственности владельцев автотранспортных средств и других видов ответственности и страховании финансовых рисков.
Нетто-ставка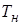 
состоит из двух частей - основной части 
и рисковой надбавки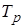 
:
. (4)
Основная часть нетто-ставки соответствует средним выплатам страховщика, зависящим от вероятности наступления страхового случая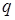 
, средней страховой суммы 
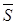и среднего возмещения 
. Основная часть нетто-ставки со 100 руб. (процентов) страховой суммы рассчитывается по формуле:
|
|
|
. (5)
Рисковая надбавка 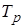вводится для того, чтобы учесть вероятные превышения количества страховых случаев относительно их среднего значения. Кроме , 
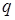и 
, рисковая надбавка зависит еще от трех параметров: 
- количества договоров, отнесенных к периоду времени, на который проводится страхование; среднего разброса возмещений 
и гарантии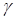 
- требуемой вероятности, с которой собранных взносов должно хватить на выплату возмещения по страховым случаям.
Возможны два варианта расчета рисковой надбавки:
1. Рисковая надбавка может быть рассчитана для каждого риска. В этом случае:
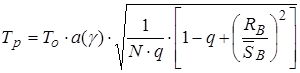, (6)
где 
- коэффициент, который зависит от гарантии безопасности 
. Его значение может быть взято, например, из таблицы:
Таблица 2.
Определение коэффициента
|
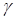
| 0,84 | 0,90 | 0,95 | 0,98 | 0,9987 |
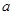
| 1,0 | 1,3 | 1,645 | 2,0 | 3,0 |
Также этот коэффициент может быть рассчитан на компьютере для любого уровня безопасности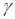 
в программе Microsoft Excel. Для этого нужно воспользоваться функцией «НОРМСТОБР(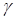)», которая возвращает обратное значение стандартного нормального распределения. - среднеквадратическое отклонение возмещений при наступлении страховых случаев. При наличии статистики выплат страховых возмещений дисперсия страховых возмещений 
оценивается следующим образом:
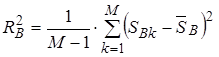. (7)
Если у страховой организации нет данных о величине , допускается вычисление рисковой надбавки по формуле:
. (8)
При наличии полной статистики по рассматриваемому договору страхования расчет рисковой надбавки может быть произведен не по формуле (6), а по формуле:
, (9)
где 
- среднее квадратическое отклонение страховых сумм:
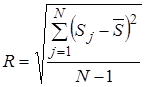. (10)
2. В том случае, когда страховая организация проводит страхование по нескольким видам рисков (
), рисковая надбавка может быть рассчитана по всему страховому портфелю, что позволяет несколько уменьшить ее размер:
, (11)
|
|
|
где 
- коэффициент вариации страхового возмещения, который соответствует отношению среднеквадратического отклонения к ожидаемым выплатам страхового возмещения. Если 
- ый риск характеризуется вероятностью его наступления 
, средним возмещением 
и среднеквадратическим отклонением возмещений 
, то:
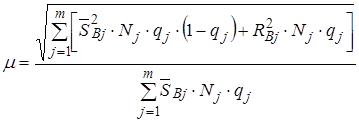, (12)
где 
- количество договоров страхования по 
– ому риску.
При неизвестной величине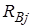 
среднеквадратического отклонения выплат при наступлении - го риска соответствующее слагаемое в числителе формулы (12) допускается заменять величиной:
. (13)
Если вычисления по формуле (12) выполнить нельзя (нет данных для расчёта 
), то коэффициент вариации 
вычисляется по формуле:
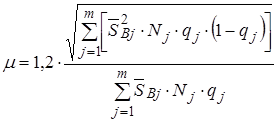. (14)
Формулы (6), (9) и (11) для вычисления рисковой надбавки тем точнее, чем больше величины 
и 
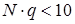. При 
и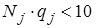 
эти формулы носят достаточно приближенный характер.
Если о величинах 
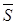, и 
нет достоверной информации, например, в случае, когда они оцениваются не по формулам (1) - (3) с использованием страховой статистики, а из других источников, то рекомендуется брать 
=3.
Брутто-ставка 
рассчитывается по формуле:
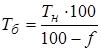, (15)
где 
(%) - доля нагрузки в общей тарифной ставке.
Расчеты страховых тарифов
3.1. Расчет тарифной ставки по страхованию имущества в программе Microsoft Excel
По предлагаемой методике расчета тарифной ставки имущественного страхования физических лиц, представленной нам в главе 2, реализована задача по нахождению брутто-ставки в программе Microsoft Excel при помощи встроенных функций. Исходные данные задачи: гарантия безопасности, y; доля нагрузки в тарифной ставке, f % и статистика по рассматриваемому виду страхования, которая включает в себя данные: о количестве договоров страхования, о средней страховой сумме по 1 договору страхования в рублях, о количестве страховых случаев, о среднем страховом возмещение по 1 договору в рублях.
Изначально необходимо внести исходные данные. Для этого требуется заполнить ячейки таблицы «Введем исходные данные» вручную.
|
|
|
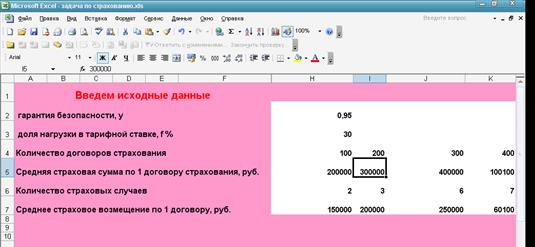
Рисунок 1- Ввод данных.
После того, как все данные введены, программа автоматически производит расчеты и выводит результат в соответствующие ячейки. Данная модель расчета позволяет рассчитать: нетто-ставку, брутто-ставку. А так же для удобства и наглядности отображаются расчеты основной части нетто-ставки, рисковой надбавки, среднего квадратического отклонения страховых сумм, дисперсии страховых возмещений.
В поставленной задаче реализован расчет тарифной ставки по трем методикам, в зависимости от предоставленной статистики.
При наличии статистики выплат страховых возмещений, вследствие чего можно рассчитать их дисперсию, расчет производится по формуле (6) из главы 2.
Рисунок 2 - Расчет по формуле (6).
В данной таблице отображаются результаты по расчету основной части нетто-ставки, которая не изменяется и используется для расчетов по другим формулам; дисперсии страховых возмещений, рисковой надбавки, нетто-ставки и брутто.
Если у страховых компаний нет данных о величине среднеквадратического отклонения возмещений при наступлении страховых случаев, расчет ставки производится по формуле (8) из главы 2.
Рисунок 3- Расчет по формуле (8).
В данной таблице отображаются результаты расчетов рисковой надбавки, нетто и брутто-ставки.
При наличии полной статистики по рассматриваемому договору страхования расчет производится по формуле (9) из главы 2.
Рисунок 4- Расчет по формуле (9).
В данной таблице отображаются результаты расчета среднего квадратического отклонения страховых сумм, рисковой надбавки, нетто- ставки и брутто.
Реализованная задача расчета тарифной ставки позволяет наглядно увидеть, как меняются значения тарифов, в зависимости от увеличения сведений в рассматриваемой статистике.
|
|
|
