Результаты пошаговой обработки эмпирических данных

ЛАБОРАТОРНАЯ РАБОТА № 1

"Определение основных параметров

Рассеивания случайных величин».

 

Цель рабо ты - исследование рассеивания размеров и оценка со­ответствия этого рассеивания назначенному полю допуска.

Задачи рабо ты - с помощью статистических методов обработки опытных данных оценить параметры рассеивания размеров.

Материалы, оборудование, инструменты: набор деталей для изме­рения исследуемого размера, мерительный инструмент (с точностью на порядок выше, чем исследуемый размер), лабораторный стол.

Порядок проведения работы

1. Провести измерения соответствующей случайной величины (по
заданию преподавателя) и зафиксировать полученные результаты изме­рений в таблице, аналогичной табл. 1.

2. Произвести обработку эмпирических данных в соответствии с
методикой, изложенной в теоретической части.

3. Построить гистограмму и полигон рассеивания исследуемой
величины.

4. Построить эмпирическое поле допуска.

5. Сделать выводы.

6. Оформить отчет о лабораторной работе.

 

Исходные данные для работы приведены в таблице 1.

 

 

Таблица I

Теоретическая часть

 

Человек обитает в предметной среде, в создании и изменении которой он сам принимает активное участие. Особенно это касается промышленного производства.

Создавая предметы труда, т.е. предметы быта и производства, человек увидел, что вещи, которые он создает, не могут быть одинаковыми. Мы знаем, что любые вновь созданные конструкция или устройства состоят из множества деталей, которые, несмотря на свою внешнюю схожесть, неодинаковы. Эту неодинаковость можно заметить, если будут применены соответствующие измерительные устройства или приборы.

Применительно к машиностроению это означает, что невозможно получить абсолютно одинаковые характеристики изготавливаемых устройств, в том числе и детали для этих устройств. Каждая характеристики, то ли интегративная (совокупная), то ли конкретная (как, например, какой-либо размер детали) получается, исходя из различных условий обработки или сборки, поэтому она будет все время стараться держаться вокруг какого-то определенного значения, но в зависимости от конкретных условий отклоняться от него или в большей, или в меньшей степени. Другими словами, любая характеристика имеет разброс. Величина этого разброса (его еще называют отклонением) задается на ранней стадии создания изделия, при его проектировании и потому реальный разброс должен быть строго определенным, т.е. укладываться в заданный допуск.

Разброс имеют не только размеры деталей. Например, числа оборотов вращения шпинделя станка, величина рабочих перемещений механизмов станков, время срабатывания какого-либо механизма, стойкость инструмента и т.д. - это величины, которые также имеют разброс.

Все величины, характеризующие точность, можно разделить на две категории. К первой относятся величины, которые колеблются в довольно узких пределах, например, число оборотов вращения шпин­деля, величина подачи станка, величина рабочих перемещений меха­низмов и инструментов. Ко второй категории относится большинство величин, особенно те, которые определяют точность изготовления. Эти величины могут изменяться в довольно широких пределах.

Величина допуска соответствует точности. Чем меньше допуск, тем выше точность.

Конструктор также задает исполнение какой-либо размера детали с допус­ком, т.е. оговаривает наибольший и наименьший размер годной дета­ли. Если при изготовлении получился размер, который лежит в интер­вале между верхним пределом и нижним пределом, то такая деталь является годной. Однако при изготовлении может быть такая ситу­ация, что только часть деталей будет годной, а другая часть имеет размеры или выше верхнего предела, или жениже нижнего предела.

Для того, чтобы количественно оце­нить разброс (рассеивание) размеров при изготовлении какой-либо детали, необ­ходимо провести экспериментальное исследование. Суть этого исследования состоит в том, что с помощью меритель­ного инструмента, точность измерения которого на порядок выше, чем измеряемый размер, устанавливается фактические размеры у группы деталей (если их изготавливается очень много) или же у всех де­талей (если их количество составляет 25 - 50 штук). В первом слу­чае говорят, что из общего числа изготавливаемых деталей (генераль­ной совокупности) произведена выборка в количестве N деталей. По выборке с определённой достоверностью можно судить о всей генера­льной совокупности. Во втором случае вся выборка - это генеральная совокупность, следовательно, достоверность полученных результатов будет составлять 100%.

Так как на значение величины влияет множество факторов, которые вами по себе являются случайными, то оценить разброс этой величины можно только с помощью вероятностных методов на основе экспериментальных исследований (измерений).

При экспериментальном исследовании определяют значения x_i, которое получается при каждом i -томизмерении. После проведения измерений, полученные значения необходимо обработать с целью определения параметров рассеивания. К этим параметрам относятся: среднее значение М и среднеквадратическое отклонение σ_x. Первый параметр характеризует положение среднего значения на оси абсцисс, а второй – меру рассеивания значений x_i вокруг М.

Значения среднего значения случайной величины М и среднеквадратического отклонения σ_x определяются по формулам

 

; (1)

 

σ_x = , (2)

 

где x_i - эмпирические (полученные опытным путем) значения случайной вёличины; i - порядковый номер измерения (i = 1, 2,.. N); N - количество измерений в выборке.

Чем больше количество информации о конкретных значениях случайной величины, тем более достоверными получаются значения М и σ_x. Однако при этомодновременно растёт объем расчетов, поэтому удобно при этом составить программу и производить расчеты на ЭВМ. Современные компьютерные программы (в том числе и Microsoft Office) имеют встроенные калькуляторы, которые имеют специальные функции для расчета как средних, так и среднеквадратических значений выборки.

Можно использовать и табличные методы расчетов исследуемых величин [1; 2].

Для наглядности строят гистограммы и полигоны рассеивания, где также представляются заданные и фактически получаемыё поля до­пусков.

Для графической интерпретации исследуемого распределения можно использовать интервальный метод обработки данных. При этом из всей выборки находят самое большое значение x_max и самое маленькое x_min, находят разницу между ними и делят её на число интервалов m, т.е.величина шага ∆ интерва­лов определяется по формуле

, (3)

где m выбирают в диапазоне от 7 до 14 и нтервалов.

Выполнение работы

1. Для определения среднего значения и среднеквадратичного отклонения размеров (табл. 1) по формулам (1) и (3) воспользуемся калькулятором программы Office.

После ввода данных в программу получили следующие значения величин:

- среднее значение – M = ……… мин,

- среднеквадратическое отклонение – σ_x = ……. мин.

2. Для графической интерпретации распределения поступим следующим образом.

Весь диапазон значений стойкостей фрез по данным таблицы 1 в соответствии с формулой (3) можно раз­бить, например, на 14 интервалов с шагом ∆ = 50 мин.

В каждом из интервалов отмечается количество «попаданий» значений случайной величины. На­пример, при принятом шаге ∆ = 50 мин в 1-ый интервал (от 0 до 50) не попало ни одно значение случайной величины (n₁ = 0), во 2-ой интервал попало 2 значения (n₂ = 2), в третий - 4 (n₃ = 4) и т.д.

Число попаданий сводим в таблицу 2, туда же заносим значения эмпирических вероятностей, которые определяем по формуле

.

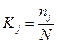Но данным таблицы 2 строим гистог­рамму (заштрихованная область на рис. 1) и полигон рассеивания (штриховая линия I), который получается соединением середин вер­шин столбцов ломаной линией,

Таблица 2

Результаты пошаговой обработки эмпирических данных

j	Интервал	Количество попаданий	Вероятность, Kj
от	до	В условных обозначениях	В числовых значения, nj

По данным таблицы 2 строим гистограмму и полигон рассеивания исследуемой характеристики. Эти диаграммы приведены на рис. 1

 

Рис. 1. Гистограмма и полигон рассеивания исследуемой величины.

 

3. Приближенно эмпирическое поле допуска может быть определено из условия, что с вероятностью 99,87% оно заключено в интервале изменения размеров в пределах ±3 σ_x oт среднего значения, поэтому достаточно на рис. 1 от среднего значения (М = ……. мин) отложить вправо и влево отрезок, численно равный (3 σ_x = ………. мин).

В Ы В О Д Ы

…………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………

Литература

1. PТМ 44-62. Методика статистической обработки эмпирических
данных. М.:Изд-во стандартов, 1962.

2. Х. В. Кордонский. Приложение теории вероятностей в инженер­ном деле. М.-Л.: Физматгиз, 1963. 435 с.

 

Контрольные вопросы

1. Oт каких факторов зависит точность выполнения размеров
деталей, например, на токарных станках?

2. Что такое существенно положительная величина?

3. Каким параметром характеризуется положение совокупности
распределения случайной величины?

4. Каким параметром характеризуется мера рассеивания слу­чайной величины?

5. Oт чего зависит степень достоверности получения парамет­ров распределения случайной величины?

6. Как можно определить приближенно эмпирическое поле допуска?

7. Для чего нужно проводить статистическую обработку эмпирических данных?

8. Что такое генеральная совокупность и что такое выборка?

Поделиться:

Воспользуйтесь поиском по сайту: