Главная | Обратная связь | Поможем написать вашу работу!

Классическая модель спиновой частицы

ЧТО ТАКОЕ СПИН?

Немного истории.

Понятие спина появилось в физике в связи с развитием квантовой механики.

В 20-х годах прошлого века физики-теоретики интенсивно размышляли над природой атомных спектров, пытаясь найти закономерности и как-то объяснить линии излучения и поглощения различных атомов. К тому времени уже существовала планетарная модель атома, в соответствии с которой атом являлся миниатюрной копией Солнечной системы: вокруг массивного и положительно заряженного ядра под действием кулоновских сил притяжения вращались отрицательно заряженные частицы – электроны. Планетарная модель атома была блестяще подтвержденная экспериментами Резерфорда (1909-1911гг.). Основная проблема, однако, состояла в том, что электрон в атоме движется с ускорением, а потому, в соответствии с законами классической электродинамики, должен излучать электромагнитные волны и как следствие терять энергию. Это излучение настолько интенсивно, что уже через триллионные доли секунды (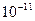 с) электрон обязан упасть на ядро. Иначе говоря, с точки зрения классической физики, атомы как стабильные частицы материи существовать не могут. Парадоксальный выход из этого затруднения был предложен великим датским физиком Нильсом Бором (1913г.). В основе теории Бора лежала планетарная модель атома, но дополненная двумя постулатами:

1-й постулат - о стационарных состояниях. В атоме существует дискретный набор орбит, вращаясь по которым электрон не излучает,
2-й постулат – о квантовых скачках. Излучение происходит только при перескоке электрона с одной стационарной орбита на другую. При этом частота излучения определяется формулой Эйнштейна 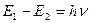, где и _- энергия начального и конечного состояния электрона, а - постоянная Планка.

Постулаты Бора (как и всякие постулаты) нельзя обосновать логически или вывести из постулатов классической физики. Тем не менее, теория Бора прекрасно объяснила линейчатость атомных спектров и некоторые другие экспериментальные факты (например, давала правильную оценку для размера атома водорода), а потому была довольно быстро принята на вооружение физиками-теоретиками. Все же, несмотря на все успехи, теория Бора не была физически последовательной и математически законченной теорией. Например, она ничего не говорила (за исключение простейшего случая – атома водорода) о том какие классические орбиты электрона нужно считать стационарными, а, следовательно, не могла предсказывать спектры сложных атомов. Все это стало возможным несколько позже после созданием Гейзенбергом (1925г.) полноценной квантовой механики. А пока, в самом начале XX века, физики изучали и систематизировали атомные спектры в надежде на то, что знание энергий переходов между различными стационарными орбитами, рано или поздно, позволит угадать общие условия, выделяющие эти самые орбиты. (К 1913г., когда Бор предложил свою модель атома, общее число работ по спектральному анализу перевалило за 50 тысяч. Так что выделить главное из общей груды экспериментальных фактов было не так-то просто.)

И чего только экспериментаторы не делали с атомами, чтобы изучить особенности их спектров. Например, помещали атом в магнитное поле. При этом каждая спектральная линия расщеплялась на несколько. Само по себе расщепление спектральных линий было открыто Питером Зееманом еще в 1896 году. Теперь, после работы Бора, его стали трактовать следующим образом: электрон, движущийся по замкнутой орбите, подобно витку провода с током создает магнитное поле, пропорциональное его орбитальному моменту . Тогда, в соответствии с законами электродинамики, внешнее магнитное поле будет стараться развернуть плоскость орбиты так, чтобы векторы и стали параллельны. Однако в отличие от витка провода с током орбита электрона (снова в духе идей Бора!) может занимать в атоме не любые положения, а лишь строго определенные. Эти орбиты характеризуются проекцией вектора на вектор . А именно: постулируется, что величина может принимать лишь целые значения: . Всего, как легко видеть, значений. В частности само абсолютное значение орбитального момента электрона должно быть целым (кратным постоянной Планка). Электрон, движущейся по каждой из орбит имеет слегка разную энергию, а потому при переходе на другую орбиту будет излучать кванты с несколько разной длиной волны. Это объяснение расщепления спектральных линий, чрезвычайно элегантное и наглядное, имеет только один небольшой изъян - оно не соответствует экспериментальным данным. Грубо говоря, число линий, на которые расщепляется каждая спектральная линия в присутствии магнитного поля, оказывалась в два раза больше, чем предсказывала теория. Это явление получило название аномального эффекта Зеемана.

Говорят, однажды Вольфганг Паули, который был очень заинтригован этой проблемой и непрерывно над ней размышлял, был остановлен на улице Копенгагена пожилой женщиной, которую поразило необычайно печальное выражение его лица. Когда она спросила Паули о причине его горя, он только покачал головой, пожал плечами и пробормотал: «Мадам, я не могу понять аномальный эффект Зеемана». (А старушке показалось, что человек только что похоронил всю семью)

В результате мучительных размышлений осенью 1924 года Паули и пришел к открытию спина электрона. Идея Паули состояла в том, что для объяснения эффекта удвоения спектральных линий нужно предположить существование у электрона, дополнительной степени свободы, но только в отличие от обычных степеней свободы, связанных с перемещением в пространстве, эта гипотетическая степень свободы может принимать лишь два возможных значения. Например, можно говорить об электроне, который в один момент времени красный, а в другой синий. При этом состояния электронов с разным цветом характеризуются различной энергией. Сам Паули называл эту степень свободы «неклассической двузначностью электрона», полагая, что наглядное представление этого свойства невозможно.

Однако уже в следующем году американские физики Джорж Уленбек и Самуэль Гаудсмит предложили наглядную модель для объяснения этого свойства электрона, предположив, что он вращается вокруг своей оси. Такая модель прямо следовала из аналогии между атомом и Солнечной системой: ведь Земля вращается не только вокруг Солнца, но и еще вокруг своей оси. Уленбек и Гаудсмит высказали гипотезу, что кроме орбитального углового момента электрону присущ внутренний момент вращения, или спин (от английского spin – веретено, вращаться), равный по величине . Подобно орбитальному моменту ориентация спина может принимать лишь дискретный ряд значений, а именно два: спин может быть ориентирован либо по полю, либо против внешнего поля. Складываясь с орбитальным моментом, этот внутренний момент может его либо увеличивать либо уменьшать. В результате возникает полный момент равный либо L+1/2 либо L-1/2 – в зависимости от взаимной ориентации векторов L и S. А это и приводит к дополнительному расщеплению спектральных линий.

Позднее спин был обнаружен и у других частиц. Например, протоны и нейтроны, подобно электронам имеют спин равный ½, фотоны (т.е. кванты электромагнитного поля) имеют спин 1, а гравитоны (кванты гравитационного поля) – 2. Вообще, спин частицы (т.е. его внутренний угловой момент) может принимать любые целые или полуцелые значения. Ирония состоит в том, что, хотя долгое время физики не догадывались о существовании спина, все известные на сегодняшний день частицы имеют ненулевой спин. А вот, казалось бы простейшая теоретическая возможность – частица без собственного углового момента, в природе почему-то не реализуется (по крайней мере такие частицы пока экспериментально не обнаружены). Тем не менее, существование таких частиц предсказывается так называемой Стандартной моделью физики элементарных частиц. Ожидается, что такие частицы, названные частицами Хиггса, будут обнаружены на открытом этой осенью большом адроном коллайдере в Церне.

Надо сказать, что выдвинутое Уленбеком и Гаудсмитом представление об электроне как о вращающемся заряженном шарике не сразу была принята физиками старой школы, поскольку находилось в разительном противоречии с принципами специальной теории относительности Эйнштейна. Расчеты, проведенные впервые Лоренцем, показывали, что скорость на экваторе вращающегося электрона должна превышать скорость света. В то время радиус электрона оценивали с помощью простой классической формулы: m_ec² ~ e²/r. Иначе говоря, считали, что масса появляется как результат электромагнитных взаимодействий. Масса электрона была достаточно хорошо измерена: m_e ~ 10^-27 г. Подставив это значение в формулу, получим r ~ 10^-13 см. Но чтобы объяснить эксперименты со спектрами, необходимо было предположить: внутренний механический момент S ~ h = 1.05 · 10^-23 эрг · сек. (Если быть точными, то S = h/2.) А тогда элементарная оценка давала: mvr ~ h и v ~ 10¹³ см/сек. В сотни раз больше скорости света c! Даже если при оценках мы ошиблись раз в десять, это не спасает.

Единственный выход из данной ситуации состоит в том, чтобы считать электрон точечной частицей, не имеющей пространственных размеров. Но тогда чем создается угловой момент электрона? Как вообще можно говорить о вращении точки? На лицо логический парадокс.

Как-то раз Эйнштейн, выступая с публичной лекцией, должен был объяснить неподготовленной публике что такое беспроводной телеграф. Радиосвязь тогда еще была в диковинку. «Сначала я объясню вам принцип работы обычного телеграфа». – начал он. «Представьте себе кошку длиной в сотню миль. Если на одном конце надавить кошке на хвост, то на другом раздастся «мяу». Так вкратце работает обычный телеграф. Беспроводной телеграф это все тоже самое, но только без кошки». Со спином история очень похожая. Представьте себе угловой момент, но без вращения.

Очень хороший рецепт избавления от противоречий состоит в том, чтобы их просто игнорировать. В соответствии с этим рецептом была принята компромиссная точка зрения: хотя свойства спина и похожи на свойства углового момента, спин все же является чисто квантовым феноменом и не может быть последовательно описан в рамках классической физики. Эту точку зрения можно найти и во многих современных учебниках и научно-популярных статьях по квантовой механике.

На самом деле это не так - наличие у точечной частицы спина не противоречит ни представлениям классической механики Ньютона, ни релятивистской механике.

Классическая модель спиновой частицы

Ключевая мысль, позволяющая разрешить парадоксы спина, состоит в том, чтобы связать спин частицы не с ее вращением в нашем 3-мерном пространстве, а с движением в некотором дополнительном внутреннем пространстве. Иначе говоря, пространство, в котором движется спиновая частица, является некоторым расширением обычного 3-мерного пространства некоторыми дополнительными (скрытыми) измерениями. При этом сама частица может предполагаться точечной, т.е. лишенной протяженности как в направлении обычных пространственных, так и дополнительных измерений. Идея дополнительных измерений не покажется такой уж странной, если встать на ту точку зрения, что вне зависимости от конкретной физической модели, спин – это, прежде всего, новая степень свободы и как любая механическая степень свободы она должна описываться некоторыми своими координатами (переменными). Изменение этих координат со временем и позволяет говорить о динамике спиновых степеней свободы.

Например, если материальная точка может совершать поступательное движение только вдоль некоторой прямой (например, бусинка на спице), то в каждый момент времени положение этой материальной точки полностью фиксируется заданием одного вещественного числа (ее координаты на прямой) и мы говорим, что эта механическая система имеет только одну степень свободы. Положение частицы, совершающей произвольное движение в плоскости (бусинка соскользнувшая со спицы и упавшая на пол) описывается двумя числами -- координатами x и y, а потому она обладает двумя степенями свободы. Наконец, обычная частица, движущаяся в 3-мерном пространстве, имеет три степени свободы потому, что для однозначного задания ее положения в каждый момент времени необходимо фиксировать три координаты x, y и z. Как мы видим добавление степеней свободы означает добавление дополнительных измерений (координат). Что же тогда удивительного в том, что для описания спина электрона необходимо расширить физическое пространство дополнительными измерениями?

Ну, хорошо, скажите вы, допустим, что все элементарные частицы имею спин. Тогда для описания их динамики надо предположить, что физическое пространство вовсе не трехмерно, а имеет какие-то дополнительные измерения. Почему же тогда мы не наблюдаем эти измерения в обычной жизни? Весь повседневный опыт убеждает нас в том, что мир, в котором мы живем, трехмерен.

Чтобы ответить на этот вопрос рассмотрим материальную точку, движущуюся по поверхности длинного и очень узкого цилиндра. Поскольку цилиндр это двумерная поверхность, наша частица имеет две степени свободы. Движение частицы по поверхности цилиндра можно разложить на две составляющие – поступательное движение вдоль оси цилиндра и вращательное движение по окружности в плоскости ортогональной оси цилиндра. Так что, в общем случае, траектория частицы будет похожа на спираль. Но если смотреть на движение частицы с очень большого расстояния (намного превышающего радиус цилиндра), то мелкие детали вращательного движения частицы будут неразличимы и вся динамика выродится в одномерное движение вдоль прямой. Иначе говоря, на макроскопических расстояниях цилиндрическое пространство выглядит как одномерное. Об этой ситуации физики говорят, что у пространства имеется одно некомпактное измерение (направление вдоль оси цилиндра) и одно компактное измерение (ортогональная ему окружность). Если радиус окружности мал, то на макроскопических масштабах (а именно масштабах на много превышающих радиус окружности) компактное измерение и отвечающая ему физическая степень свободы практически не наблюдаемы. Оно «оживает» и становится существенным только при переходе на микроскопический уровень (т.е. масштабы сравнимые с радиусом окружности). Если хотите, приведенная модель может рассматриваться в качестве игрушечной модели спиновой частицы «живущей» в одномерном пространстве. При этом спин частицы естественным образом отождествляется с ее угловым моментом относительно оси цилиндра, т.е. с возможностью совершать движение вдоль компактного (а потому макроскопически ненаблюдаемого) измерения. И только при переходе на микроуровень живущий в этом мире исследователь вдруг обнаружит, что частицы, из которых построен его мир, имеют спин, а само пространство – дополнительное измерение.

Совершено аналогичная картина имеет место и в случае нашего трехмерного пространства, с той только лишь разницей, что для описания спина трехмерной частицы необходимо добавить два измерения, имеющих форму двумерной сферы. Радиус сферы оказывается пропорциональным h, и ввиду исчезающей малости постоянной Планка эти дополнительные измерения могут наблюдаться (проявляться) лишь на микроскопическом уровне при исследовании свойств атомов и молекул.

Предвижу естественный вопрос: А почему собственно для описания спина трехмерной частицы добавляется именно два измерения, а скажем не одно или три, и почему их надо организовать в двумерную сферу, а не в поверхность бублика (которая в математике называется тором) или в поверхность кренделя с двумя дырками (не имеющую специального названия), да мало ли какие еще существуют двумерные компактные поверхности?

Выбор двумерной сферы в качестве пространства спиновых степеней свободы, конечно же, не случаен. Более того, для 3-мерной спиновой частицы он является единственно возможным. Но чтобы обосновать этот выбор нам придется вернуться к самым первым принципам классической механики и ответить себе на вопрос, а что же такое элементарная частица с самой общей точки? Можно ли придать понятию «элементарность» некоторый формальный математический смысл?

Если кому-то этот вопрос вдруг покажется чересчур абстрактным или пустым, то это только оттого, что он над ним не достаточно размышлял. Действительно, на первый взгляд все очень просто: каждый школьник знает, что элементарная частица (если на минуточку забыть про спин) эта просто материальная точка, движущаяся в пространстве, причем в рамках механики Ньютона ее динамика описывается системой дифференциальных уравнений

Если на частицу не действуют внешние силы (F=0), то эти уравнения имеют элементарное решение, описывающее прямолинейное равномерное движение

, , .

Задание начального положения и скорости частицы в начальный момент времени t=0 полностью определяет вид решения уравнений движения (т.е. траекторию частицы). Это верно и для свободной частицы и для частицы находящейся под действием внешних сил. Поэтому говорят, что задание мгновенного положения и мгновенной скорость частицы определяет ее состояние. Если известно состояние частицы в какой-то начальный момент времени, то, используя уравнения движения, мы можем определить ее состояние и во все последующие (а заодно и предыдущие) моменты времени, т.е. определить ее движение. Здесь важно уяснить себе, что для фиксации состояния частицы не достаточно задать только ее положение в пространстве – состояние это положеиие + скорость, т.е. набор из шести чисел (x, v). Таким образом, число параметров описывающих оказывается состояние механической системы в два раза больше числа степеней свободы. В частности, число этих параметров оказывается всегда четным.

Вопрос: Откуда видно, что эти уравнения описывают движения одной материальной точки в трехмерном пространстве? Ведь с тем же успехом можно сказать, что они описывают движение трех частицы на прямой (координата первой обозначена x, второй - y, а третей - z). При этом в последнем случае, данную механическую систему уже нельзя считать элементарной – она состоит из совокупности трех элементарных частиц в одномерном пространстве. Аналогичным образом мы могли бы начать с уравнений, описывающих динамику двух материальных точек в 3-мерном пространстве, а затем интерпретировать их как уравнение для одной материальной точки в шестимерном пространстве. Заметим, что при любой интерпретации одной и той же системы уравнений общее число степеней свободы остается неизменным, однако такое фундаментальное понятие как размерности физического пространства вроде бы утрачивает инвариантный смысл. Глядя только на уравнения движения, нельзя с уверенностью сказать в какое физическое пространство погружены механические степени свободы, описываемые этим уравнением. Как следствие, теряет смысл и само понятие элементарности механической системы.

На самом деле, вне зависимости от конкретного вида, уравнения Ньютона «знают» в каком пространстве развивается динамика. И это знание связано вовсе не с тем, что пространственные степени свободы, относящиеся к одной частицы, вы помечаете одинаковым индексом (1,2,…), а с тем, что сами уравнения движения обладают определенными симметриями, отражающими фундаментальные симметрии пространства и времени. Постулат о существовании этих симметрий известен как принцип относительности Галилея. Наличие этих симметрий с одной стороны накладывает некоторые ограничения на возможной вид уравнений движения, а с другой - позволяет придать объективный смысл таким понятиям как «размерность физического пространства» и «элементарная частица».

Напомню, что первый закон Ньютона постулирует существование так называемых инерциальных систем отсчета, т.е. таких систем координат в которых свободное движение тел происходит с постоянной скоростью. Ясно, что из существования одной инерциальной системы отсчета вытекает существование их бесконечного количества. Например, мы можем сдвигать начало координат инерциальной системы отсчета или поворачивать ее в пространстве на некоторый угол в результате будет получаться некоторая новая инерциальная система отсчета, поскольку всякое свободное движение в этой новой системе координат будет также прямолинейным и равномерным. Свойство прямолинейности и равномерности свободного движения не нарушится, если мы перейдем в систему отсчета, движущуюся относительно первой с некоторой постоянной скоростью V. Так вот принцип относительности Галилея утверждает, что все законы движения одинаковы во всех инерциальных системах отсчета. Иначе говоря, во всех механических отношениях инерциальные системы полностью эквивалентны, так что, наблюдая за движением тел, мы не можем отличить одну инерциальную систему отсчета от другой.

Можно показать (попробуйте сделать это сами) что все перечисленные выше преобразования – сдвиги начала отсчета, повороты осей координат, а также придание началу отсчета некоторой постоянной скорости – исчерпывают все преобразования, переводящие инерциальные системы отсчета в инерциальные. Эти преобразования называются преобразованиями Галилея. Поскольку преобразования Галилея не меняют вид уравнений движения, то о них также говорят как о преобразовании симметрии механической системы. (Обычно в определение системы отсчета включают также и часы. Тогда сдвиг начала отсчета времени является еще одним преобразованием симметрии. Но для нашего обсуждения наличие последней симметрии не буде играть существенной роли, а потому мы будем считать, что способ отсчета времени раз и на всегда фиксирован.)

Легко подсчитать, что самое общее преобразования Галилея (не затрагивающее время) описывается 9 параметрами (3 пространственных сдвига, 3 поворота и 3 компоненты вектора скорости V). Об инвариантности движения относительно сдвигов говорят как об однородности пространства, т.е. равноправности (одинаковости) всех точек пространства. Инвариантность относительно поворотов является следствием изотропности пространства, т.е. равноправность всех пространственных направлений.

Несколько особняком стоит преобразование, связанное с переходом в движущуюся систему отсчета, поскольку это преобразование изменяет не только пространственные координаты, но и скорость частицы. Поэтому для того, чтобы трактовать все эти преобразования единообразно полезно рассмотреть их действие не на координаты частицы, а на ее состояния. Легко видеть, что самое общее преобразование Галилея действует на состояние частицы в начальный момент времени t=0 по формуле

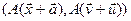где A – есть матрица, задающая повороты в пространстве, а – вектор сдвига начала координат, u – скорость системы отсчета. Заметим, что, используя преобразования Галилея, мы можем перевести любое начальное состояние частицы в любое другое ее состояние. Другими словами, любые два начальных состояния оказываются связанными некоторым преобразованием Галилея. Об этой ситуации говорят, что преобразования Галилея действуют транзитивно на пространстве состояний механической системы. Если же мы рассмотрим механическую систему, состоящую из двух частиц, то свойство транзитивности уже не будет иметь место.

Теперь, уже не трудно сообразить, что транзитивность пространства состояний по отношению к преобразованиям Галилея и есть то самое свойство, которое следует положить в основу определения элементарности частицы. А именно:

Элементарной частицей называется механическая система, пространство состояний которой транзитивно относительно действия галилеевских преобразований симметрии.

Если принять это определение, то из него следует очень важной вывод: невозможно определить понятие элементарной частицы или «элементарности» как таковой не сказав предварительно какими фундаментальными симметриями должно обладать ее пространство состояний. И только после того как симметрии фиксированы, это понятие приобретает инвариантный смысл. Опыт показывает, что такие фундаментальные физические симметрии действительно существуют в природе и что все они исчерпываются преобразованиями Галилея.

Ввиду своей фундаментальности преобразования Галилея должны действовать в пространстве состояний любой механической системы (не важно элементарной или не элементарной), в том числе и в пространстве состояний частицы со спином. Последнее требование, как оказывается, накладывает очень жесткие ограничения на возможный вид пространства состояний спиновых степеней свободы. Действительно, довольно очевидно, что для того чтобы преобразования Галилея действовали транзитивно в пространстве состояний, размерность этого пространства не должна превышать числа параметров, от которых зависит общее преобразование Галилея. Но общее преобразование Галилея, как мы видели, зависит от 9 параметров. Поскольку пространство состояний частицы без спина уже 6-мерно, то состояние спина может описываться самое большее тремя параметрами, т.е. может быть одно, двух или трехмерным. Мы также знаем, что пространство состояний должно быть четномерным (каждой координате отвечает своя скорость), а это оставляет только одну теоретическая возможность – его размерность равна двум. Остается определить форму этого пространства. После того, как положение частицы в пространстве и ее скорость приведены к некоторому фиксированному виду, у нас в распоряжении остаются только пространственные повороты. Таким образом, наша двумерная поверхность должна переходить в себя под действием пространственных поворотов. Замечательный математический факт состоит в том, что имеется ровно одна двумерная компактная поверхность, точки которой могут транзитивно преобразовываться друг в друга под действием пространственных вращений – это двумерная сфера.

Таким образом, сама возможность существования в природе частиц со спином является прямым отражением того фундаментального факта, что физическое пространство обладает некоторыми симметриями. Не будь этих симметрий, было бы невозможно говорить не только о спиновых частицах, но и об элементарных частицах вообще.

После того как пространство состояний спиновой частицы установлено, уже не трудно написать и уравнения движения, описывающие свободное движение. Например, имеется такая простейшая возможность:

, , , .

На самом деле, ни каких других уравнений для спиновой частицы, которые сохраняли свою форму при преобразованиях Галилея написать нельзя. Иначе говоря, этот вид уравнений однозначно фиксируется требованиями симметрии. Эти уравнения говорят нам о том, что свободная спиновая частица движется равномерно прямолинейно, при этом ее положение на сфере не меняется (вектор спина сохраняет ориентацию). Если мы отождествляем вектор s со спином частицы, то в классической теории его длина r может быть любой. Однако в квантовой теории радиус сферы может принимать лишь дискретный ряд значений: , . Ввиду исчезающей малости постоянной Планка, для не очень больших s наша сфера будет иметь очень маленький радиус, а потому связанные с ней дополнительные измерения будут макроскопически не наблюдаемы.

Если частица находится под воздействием внешних сил, то в правые части уравнений движения надо добавить соответствующие выражения. Вид этих выражений не может быть установлен на основе общих рассуждений, а зависит от конкретной модели взаимодействия. Например, если на частицу действуют внешние электрические и магнитные поля, то в правой части второго уравнения появляется сила Лоренца и похожее выражение можно добавить в правую часть третьего:

, .

Заметим, что эти уравнения согласованы с требованием, чтобы абсолютная величина спина сохранялась со временем. Если электрическое поле E равно нулю, а магнитное поле H постоянно, то заряженная частица движется по спирали в пространстве, при этом вектор спина s совершает круговое движение на сфере. Если в правую часть первого уравнения добавить дополнительное слагаемое , то получим нерелятивистские уравнения Баргмана-Мишеля-Телегди. Видно, что в случае неоднородного магнитного поля наличие спина влияет на траекторию частицы в x-пространстве (она начинает колебаться в окрестности траектории, описывающее динамику беспиновой частицы). Это явление получило название Zitterbewegung (нем. - дрожание).

Релятивистское обобщение
Проблема высших спинов

Воспользуйтесь поиском по сайту: