Концепции измерения радиоактивных препаратов и их излучений

Лабораторная работа №7

ИЗУЧЕНИЕ НОРМАЛЬНОГО ЗАКОНА РАСПРЕДЕЛЕНИЯ СЛУЧАЙНЫХ ВЕЛИЧИН И ЕГО ОСНОВНЫХ ХАРАКТЕРИСТИК

I. Цель работы: Ознакомиться с законом распределения случайных величин, построить гистограмму, научиться статистически обрабатывать результаты измерений.

II. Приборы и принадлежности: Персональный компьютер, дозиметр – радиометр «Сосна»

III. Теоретическая часть:

Концепции измерения радиоактивных препаратов и их излучений

Активность радиоактивного препарата определяется числом атомных сред, распределяющихся в препарате в единицу времени. В СИ единицей активности является беккерель (Бк) (1 Бк=1 распад/с). Допускается применение внесистемных единиц измерения активности: распад/мин и кюри (Ки) (1Ки=3,7×10¹⁰ распад/с, 1мКи=10^-3Ки, 1мкКи=10^-6Ки). Удельной активностью называется активность единицы массы радиоактивного вещества.

Доза рентгеновского или гамма-излучения есть мера излучения, основанная на его ионизирующей способности. За единицу дозы излучения принята такая доза, при которой сопряженная корпускулярная эмиссия на 1,293×10^-6кг воздуха производит в воздухе ионы, несущие электрический заряд: 1/(3×10⁹) кулон каждого знака. Эта единица дозы называется рентгеном (Р). Мощностью дозы излучения называется величина дозы в единицу времени. Основной единицей мощности дозы является рентген в секунду (Р/с).

Дозой излучения можно характеризовать лишь ионизирующее действие электромагнитного излучения в воздухе. Универсальной характеристикой действия любой ионизирующей радиации в веществе является поглощенная доза, которая равна энергии ионизирующего излучения, поглощенной единицей массы облучаемого вещества. Единицей измерения поглощенной дозы является рад (1рад=0,01Дж/кг).

Известно, что при одинаковом количестве энергии, выделяющейся в биологической ткани, различные виды ионизирующей радиации производят неодинаковое биологическое действие на организм. Поэтому вводится понятие биологического эквивалента (бэр). Биологическим эквивалентом рентгена называется количество энергии любого вида излучения, поглощенное в живой ткани, биологическое действие которого эквивалентно действию одного рентгена рентгеновских или гамма-лучей.

При любом физическом измерении результат, полученный на опыте, несколько отличается от действительного значения измеряемой величины. Погрешности измерений складываются из ошибок, связанных с несовершенством методики измерений и неточностью колибровки приборов (эти ошибки принято называть систематическими), и из случайных ошибок эксперимента, изменяющих свою величину и знак от опыта к опыту. Частным случаем ошибок являются так называемые статистические ошибки. Эти ошибки называются флуктуациями самой измеряемой величины. К числу флуктуирующих величин относится и интенсивность космического излучения. Пусть при некотором измерении за 10с зарегистрировано n космических частиц. Из этого отнюдь не следует, что в любые следующие 10с будет регистрироваться именно n частиц. В силу случайных причин при этом можно получить n-1, n+2 или любое другое, вообще говоря, не слишком сильно отличающееся от n число. В этом случае, как и всегда при измерении флуктуирующих величин, физический смысл имеет не столько результат отдельного измерения, сколько средний результат опыта, в нашем примере – среднее количество частиц, проходящих через установку за 10с (или в 1с).

Чтобы определить среднюю интенсивность космических частиц, следует измерить число частиц, прошедших через установку за большое время, и разделить полученное число на время измерения и площадь счетчика (под интенсивностью излучения понимается число частиц, проходящих через единичную площадку в единицу времени). Строго говоря, средняя интенсивность равна пределу, к которому стремятся полученные таким образом числа при неограниченном увеличении времени измерения. Отдельные измерения, проведенные в течение некоторого конечного и, как правило, не слишком большого отрезка времени, позволяют определить искомую среднюю интенсивность излучения не вполне точно, а с некоторой ошибкой, величина которой нем меньше, чем больше время измерения.

Рассмотрим более внимательно опыт по определению интенсивности космических лучей. При небольших размерах установки и не очень большом времени, которое можно использовать для опыта, все ошибки оказываются пренебрежимо малыми по сравнению со статистическими флуктуациями, поэтому никаких других отклонений, кроме статистических, мы рассматривать не будем.

Проведем ряд опытов по измерению числа частиц, попадающих в счетчик за фиксированное время t. Сравнив полученные результаты, мы увидим, что данные числа заметно отличаются друг от друга, хотя среди них встречаются и одинаковые. Построим график, откладывая по оси абсцисс число частиц, зарегистрированных при измерениях, а по оси ординат – долю случаев (по отношению к общему числу измерений), в которых было зафиксировано данное количество частиц. Построенный график содержит дискретно расположенные точки, которые для наглядности обычно соединяют между собой. Лучше всего это делать, представляя график в виде совокупности вертикально стоящих прямоугольников, как это изображено на рис.1. На этом графике прямоугольник, расположенный между 0 и 1, характеризует случаи, в которых регистрировалось 0 отсчетов; прямоугольник расположенный между 1 и 2, случаи с одним отсчетом и т.д. Высота прямоугольника определяет долю наблюдаемых случаев w_n (иногда вместо доли случаев на графике изображается их число). Подобного рода график принято называть гистограммой.

Мы получим, таким образом, график распределения результатов опыта, который обнаруживает максимум в области искомого среднего значения, хотя среди результатов попадаются и такие, которые сильно отличаются от среднего. Доля случаев, в которых происходит некоторое событие, (например, обнаруживается данное число отсчетов), называется вероятностью этого события.

Построенный график (гистограмма), таким образом, характеризует распределение вероятности зарегистрировать n частиц за время t в зависимости от величины n. Обозначим среднюю, (вообще говоря, нам не известную) интенсивность космических лучей буквой у. Среднее количество n ₀ частиц, проходящих через счетчик за время t при очень большом полном времени измерений равно, очевидно yt = n ₀.

Хотя число отсчетов счетчика, измеренное за любое время представляется целым числом, среднее значение не обязательно должно быть целым.

На рис.1 представлена зависимость w_n с n при различных значениях n₀. По мере роста n₀ максимум графика сдвигается более симметричным относительно точки n = n₀. Для сравнения различных распределений по ширине выбраны такие масштабы по оси абсцисс, чтобы положения максимумов у всех гистограмм совпадали. При малых n₀ график резко асимметричен. Из рисунка видно, что при всяком n₀ можно получить в результате измерений самые разные значения n, но не все эти значения встречаются одинаково часто. Если величина n близка к n₀, то вероятность w_n велика, а при удалении n и n₀ она быстро падает.

На самом деле многократные измерения производятся редко. Наибольший интерес представляет ожидаемое отличие результата, полученного при одиночном измерении, от истинного значения. Приведенные рассуждения с серией измерений служат для пояснения именно этого вопроса. При однократном измерении отклонение результата от истинного, в зависимости от случая, может быть большим или меньшим, но чаще всего оно по порядку величин равно полуширине кривой распределения w_n (полуширина распределения обычно измеряется на половине высоты). Эта полуширина характеризует поэтому точность однократного измерения.

Чем уже распределение, тем с большим основанием можно утверждать, что найденное на опыте значение может быть отождествлено с искомым средним. Чем распределение шире, тем меньше оснований для такого отождествления.

Для оценки точности измерений обычно применяют величину называемую дисперсией. Дисперсией s² случайной величины называется среднее значение квадрата отклонения этой величины от ее среднего значения: s² = (n-n₀)². Сама величина (корень квадратный из дисперсии) называется среднеквадратичной ошибкой или стандартным отклонением.

В теории вероятности показывается, что при достаточно большом числе отсчетов в 2/3 случаев (с вероятностью 68%) истинное среднее значение отличается от результатов измерения не более чем на одну среднеквадратичную ошибку (±s) и с вероятностью 95% не более чем на две среднеквадратичные ошибки (±2s).

Из теории следует, что среднеквадратичная ошибка отсчетов, измеренного на некоторый интервал времени, равна корню квадратному из среднего числа отсчетов за тот же интервал: 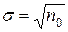. Однако истинное среднее значение переменной величины неизвестно (иначе для его определения не пришлось бы ставить опыты). Поэтому в формулу для определения стандартной ошибки отдельного измерения приходится подставлять не истинное среднее значение n ₀, а измеренное значение n: (1). Формула (1) показывает, что как правило, (с вероятностью 68%) измеренное число частиц n отличается от искомого среднего не более чем на . Результат измерений записывается так: (2).

Обратимся теперь к следующему важному вопросу. Пусть мы провели серию из N измерений, в результате которой получены числа частиц n ₁, n ₂, …, n_N. Эти результаты мы до сих пор использовали для того, чтобы определить, как сильно значения, полученные в отдельных измерениях, отличаются от истинного значения. Как уже отмечалось, этот вопрос важен главным образом для выяснения того, насколько достоверен результат, полученный в одном измерении. Но если было проведено несколько измерений, их результаты могут быть использованы и с другой целью: они позволяют определить среднее значение измеряемой величины лучше, чем это можно сделать, если произведено всего одно измерение. При N измерениях среднее значение числа сосчитанных за одно измерение частиц равно, очевидно,

, (3)

а стандартная ошибка отдельного измерения, по определению, равна

. (4)

В соответствии с формулой (1) следует ожидать, что эта ошибка будет близка к , т.е. , где в качестве n_l можно подставить любое из измеренных значений n. Поскольку n_l различны, мы будем, таким образом, получать для различные оценки. Одни из них будут лучше, а другие хуже совпадать с более надежной оценкой - со значением, определенным по всем измерениям, т.е. по формуле (4). Это вполне естественно. Обрабатывая результаты измерений, мы всегда получаем приближенные значения измеряемой величины и приближенные значения погрешностей, которые, в зависимости от случая, могут лучше или хуже совпадать с истинными. Ближе всего к значению определенному по формуле (4) лежит, конечно, величина , т.е. (5).

Величина из формулы (3), полученная путем усреднения результатов серии из N опытов, конечно, тоже не вполне точно совпадает с истинным средним значением n ₀ и сама является случайной величиной. Теория вероятностей показывает, что стандартная ошибка отклонения от n ₀ может быть определена по формуле

. (6)

Обычно наибольший интерес представляет не абсолютная, а относительная точность измерений. Для серии из N- измерений относительная ошибка отдельного измерения (т.е. ожидаемое отличие любого из n_l от n ₀)

.

Аналогичным образом определяется относительная ошибка в определении среднего значения по всем измерениям:

. (7)

Таким образом, относительная точность измерения определяется только полным числом отсчетов и не зависит от интервалов разбиения серии (по 10, 40 или 100с). Этого, конечно, и следовало ожидать, так как все измерения вместе составляют одно более продолжительное измерение, в котором всего зарегистрировано отсчетов. Как мы видим, относительная точность измерения постоянно улучшается с увеличением числа отсчетов (значит, и с увеличением полного времени измерений).

С помощью формулы (7) найдем, что для измерения интенсивности космического излучения с точностью до 1% нужно получить, по крайней мере, 100²=10000 отсчетов, для точности 3% достаточно 1000 отсчетов, при точности 10% нужно всего 100отсчетов и т.д. При этом точность измерения не зависит от того, получены ли все 1000 или 10000 отсчетов в одном или в нескольких независимых опытах.

 

IV. Порядок выполнения работы:

 

Для экспериментального исследования закона распределения случайных величин используется прибор «Сосна», при помощи которого мы будем регистрировать количество b-частиц, попавших на детектор. Компьютерная обработка результатов измерений статистики импульса осуществляется с помощью программы-счетчика Sosna по следующей схеме:

1. Открыть заднюю крышку прибора сосна и положить прибор на стеклянную пластинку открытой стороной к пластинке.

2. Включить прибор сосна.

3. Запустить программу счета импульсов Sosna в директории d:\sound\sosna.exe. Примечание. При запуске программы с выключенным прибором «Сосна» может произойти аварийное завершение программы. Для запуска программы необходим определенной уровень сигнала на входе звуковой карты компьютера, который и обеспечивается стеклом. При измерении фона уровень сигнала недостаточно высок, и нужно подкладывать стекло для запуска программы. После успешного запуска стекло можно убирать.

4. Программа работает следующим образом. После запуска она начинает счет импульсов. Число импульсов и время регистрации последнего импульса отображаются в нижнем окне программы, осциллограмма сигнала счетчика – в верхнем. При нажатии кнопки Stop происходит сброс счетчика и запись моментов регистрации импульсов в файл intervals.txt, который находится в той же папке, что и программа. При этом кнопка меняет свое название на Start. Внимание! Файл с данными перезаписывается заново каждый раз после сброса программы (а именно, после нажатия кнопки Stop), поэтому, желательно вручную переименовывать его перед последующим запуском программы-счетчика. Повторный запуск осуществляется нажатием кнопки старт.

5. Файл данных содержит времена регистрации импульсов счетчика в секундах от момента запуска программы (при первом измерении) или от момента нажатия кнопки Start. Файл обрабатывается с помощью документа Matcad hist2001.mcd в этой же папке. В нем имеются необходимые пояснения.

 

Поделиться:

Воспользуйтесь поиском по сайту: