 |
Связь между автоматами Мили и Мура
|
|
|
|
Для любого автомата Мили можно построить эквивалентный ему автомат Мура и, обратно, для любого автомата Мура можно построить эквивалентный ему автомат Мили.
Рассмотрим преобразование автомата Мили в автомат Мура. Пусть задан автомат Мили S = (A, Z, W, d, l, a 1 ), построим автомат Мура
S / = (A /, Z /, W /, d /, l /, a 1/ ), у которого Z / = Z; W / = W.
Для определения множества A / необходимо выполнить расщепление состояний автомата Мили исходя из следующего. Если автомат Мили при переходе в некоторое состояние as может выдавать в разные моменты времени один из  выходных сигналов из алфавита W, то такое состояние as должно быть расщеплено на
выходных сигналов из алфавита W, то такое состояние as должно быть расщеплено на  состояний. То есть число элементов в множестве As равно числу различных выходных сигналов на дугах автомата S, входящих в состояние as (рис.3.8):
состояний. То есть число элементов в множестве As равно числу различных выходных сигналов на дугах автомата S, входящих в состояние as (рис.3.8):
As = {(as, w 1), (as, w 2), (as, w 3),..., (as, wk)}.
 As = {(as, w 1), (as, w 2), (as, w 3)}
Рис.3.8. Построение множества As
As = {(as, w 1), (as, w 2), (as, w 3)}
Рис.3.8. Построение множества As
|
Множество состояний автомата S / получим как объединение множеств As:
A /  ,
,
где M – число состояний в автомате Мили S.
Такое расщепление состояний автомата Мили необходимо потому, что все состояния эквивалентного ему автомата Мура должны быть отмечены только одним выходным сигналом из алфавита W.
Функцию переходов d / и выходов l / определим следующим образом. Если в автомате Мили S был переход d (am, zf) = as и при этом выдавался выходной сигнал l (am, zf) = wg, то в автомате Мура S / (рис.3.9) будет переход из множества состояний Am, порождаемых am, в состояние (as, wg) под действием того же входного сигнала zf.
В качестве начального состояния автомата Мура  можно взять любое состояние из множества A 1, порождаемого начальным состоянием a 2.
можно взять любое состояние из множества A 1, порождаемого начальным состоянием a 2.

Рис.3.9. Иллюстрация перехода от автомата Мили к автомату Мура
|
|
|
Пример3.4. Преобразовать автомат Мили, изображенный на рис.3.7,а, в автомат Мура.
Решение.
Для автомата Мура Z / = Z = { z 1, z 2};
W / = W = { w 1, w 2, w 3, w 4, w 5}.
Построим множество А / для чего найдем множества пар порождаемых каждым состоянием автомата Мили S. Каждую пару обозначим символами b 1, b 2, ...:
A 1 = {(a 1, w 2),(a 1, w 4)} = { b 1, b 2}; A 2 = {(a 2, w 1)} = { b 3};
A 3 = {(a 3, w 3),(a 3, w 5)} = { b 4, b 5}; A 4 = {(a 4, w 4),(a 4, w 5)} = { b 6, b 7}.
A / = { b 1, b 2, b 3, b 4, b 5, b 6, b 7}.
Для определения функции l / с каждым состоянием вида (as, wg),
представляющим собой пару, отождествим выходной сигнал, являющийся вторым элементом этой пары:
l /(b 1) = w 2; l /(b 2) = l /(b 6) = w 4; l /(b 3) = w 1;
l /(b 4) = w 3; l /(b 5) = l /(b 7) = w 5.
Поясним построение функции d /.
Так как в автомате Мили S есть переход из состояния a 1 под действием сигнала z 1, в состояние a 2 с выдачей w 1, то из множества состояний A 1 = { b 1, b 2}, порождаемых а 1 в автомате S / должен быть переход в состояние (a 2, w 1) = b 3 под действием сигнала z 2. Аналогично из состояний множества A 1 = { b 1, b 2} должен быть переход в состояние
(a 4, w 5) = b 7 под действием сигнала z 2 и т.д.
В качестве начального состояния можно выбрать одно из состояний, порождаемых а 1, например, b 2.
На рис.3.10 приведен граф автомата Мура S /, эквивалентного автомату Мили S. Табл. 3.13 - отмеченная таблица переходов автомата Мура  .
.
Таблица 3.13
Отмеченная таблица переходов S /
| W / | w 2 | w 4 | w 1 | w 3 | w 5 | w 4 | w 5 |
| A / | b 1 | b 2 | b 3 | b 4 | b 5 | b 6 | b 7 |
| z 1 | b 3 | b 3 | b 3 | b 1 | b 1 | b 2 | b 2 |
| z 2 | b 7 | b 7 | b 4 | b 6 | b 6 | b 5 | b 5 |

Рис.3.10
Граф автомата Мура S /
Запишем отмеченную СКУ (3.15) и СВФ (3.16) для автомата Мура  эквивалентного автомата Мили
эквивалентного автомата Мили  .
.
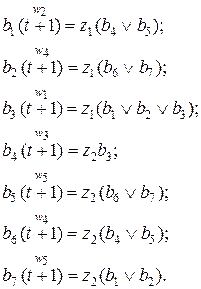 (3.15) (3.15)
|  (3.16) (3.16)
|
Рассмотрим теперь переход от произвольного автомата Мура к эквивалентному ему автомату Мили. Этот переход при графическом способе задания иллюстрируется рис.3.11: выходной сигнал (wg), записанный рядом с вершиной (as), переносится на все дуги, входящие в эту вершину.

Рис.3.11. Иллюстрация перехода от автомата Мура к автомату Мили
|
|
|
При табличном методе задания выполняется преобразование отмеченной таблицы переходов исходного автомата Мура. При этом в совмещенную таблицу переходов автомата Мили вместе с состояниями записываются отмечающие их выходные сигналы. Затем выполняется минимизация числа состояний автомата Мили.
|
|
|


