Знакомство с характеристики источников ЭМ поля

2012

 

Особенности моделирования макроскопических систем (вещества). В 1 кубическом см твердого тела содержится примерно 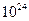молекул. Если рассматривать вещество как совокупность реальных материальных частиц, то численное изучение ЭМ явлений становится практически невозможным; для получения количественных результатов прибегают к методам и моделям механики сплошной среды.

В большинстве макроскопических явлений, изучаемых в электродинамике, участвует громадное число электрических зарядов, и их дискретность никак не проявляется. Поэтому в большинстве случаев можно считать, что заряд как бы непрерывно распределен в пространстве (наподобие жидкости), и не принимать во внимание его дискретность.

Базовые принципы механики сплошной среды. Использование непрерывного, сглаженного описания. Считается, что вещество как бы «размазывается» и заполняет пространство непрерывным образом, без каких-либо пустот; происходит абстрагирование от реального (атомно-молекулярного) строения тел и переход к идеализированному представлению вещества в виде некоего материального континуума. Эту субстанцию можно разбить на большое число элементов (частиц среды-континуума), размеры которых малы по отношению к геометрическим размерам всего моделируемого объекта, но большие по сравнению с размерами молекул. Объем такого элемента, очевидно, есть так называемый физически бесконечно малый объем .

Физически бесконечно малый объем [7, c.34-42]. Объем является бесконечно малым не в математическом, а в физическом смысле:

-а) он настолько мал8, что положение в пространстве достаточно точно характеризуется координатой любой его внутренней точки

-б) внутри объема должно находиться достаточно много элементарных зарядов, чтобы небольшое смещение элемента не приводило к существенному изменению плотности заряда.

Или

,

где - среднее расстояние между заряженными частицами в объеме, - характерный размер макроскопического объекта ( - объем объекта).

Можно сказать: - малый в смысле (а) объем, который, тем не менее, можно рассматривать как элемент сплошной среды.

Таким образом, зависит от конкретных условий. Иногда встречаются ситуации, когда объема , который можно считать физическим бесконечно малым, не существует. В этом случае пользоваться представлением о непрерывном распределении заряда нельзя9.

Вернемся к модели материального континуума. Сплошной средой (или континуумом) можно считать не только обычные (деформируемые) материальные тела, но и ЭМ поле, и энергию, и электрический заряд. Именно благодаря такой идеализации удается привлечь для моделирования реальных физических объектов математический аппарат дифференциального и интегрального исчисления непрерывных функций (понятий бесконечно малой, предельного перехода и др.)

Количественное описание физического объекта, который моделируется как сплошная среда, осуществляется на основе математических полей скалярных и векторных величин. Математическое поле – скалярная или векторная функция точки, например, , где – радиус-вектор точки исследуемой области пространства (точки наблюдения), - время.

Основные характеристики, описывающие состояние электрического заряда в приближении сплошной среды, это объемная плотность заряда , объемная плотность тока , скорость переноса заряда . Это локальные (дифференциальные) характеристики.

Объемная плотность заряда 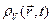определяется так, чтобы величина была равна заряду, находящемуся в момент времени в физически бесконечно малом объеме (элементе эквивалентной сплошной среды) , содержащем точку . В этом случае

= (1)

или

.

Здесь суммирование распространяется на все (элементарные) заряды , находящиеся в момент времени в объеме . Очевидно, что интеграл

(2)

по любому объему равен полному заряду в этом объеме в момент времени .

Заметим, что можно говорить о плотности зарядов определенного знака:

= + .

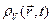Концентрация () зарядов определенного знака определяется так, чтобы величина 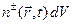была равна числу зарядов соответствующего знака, находящемуся в момент времени в физически бесконечно малом объеме (элементе эквивалентной сплошной среды) , содержащем точку . В этом случае

(3)

или

.

Пусть рассматриваются частицы с одинаковыми положительными зарядами (элементарный заряд ) и с одинаковыми отрицательными зарядами (элементарный заряд 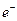). Тогда

 

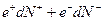= , (4)

где , 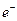- элементарные заряды. Следовательно,

 

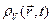= = + . (5)

 

Пример 1. Непрерывное распределение заряда в пространстве. Объемная плотность заряда может быть задана непрерывнойфункцией координат. Например,

,

где есть постоянная величина. Это означает, что заряд по всему пространству распределяется с одинаковой плотностью. Такой случай на практике не реализуется и далее в теории не рассматривается. Практически имеют смысл лишь заряды конечной величины, так что

(интеграл берется по всему пространству.) Например,

,

где .

 

Упражнение. Конечный заряд распределен во всем пространстве с плотностью

,

где . Найдите этот заряд.

 

Пример 2. Кусочно-непрерывное распределение заряда в пространстве. Такое распределение типично для практики. Заряд с плотностью распределен в некоторой области пространства. В соседней с нею области плотность заряда описывается другой функцией . На границе областей (поверхность )объемная плотность заряда может измениться скачком на конечную величину. (Это, конечно, всего лишь математическая модель: в рамках подхода сплошной среды плотность заряда не может иметь скачков, она непрерывна.). Так, например, объемная плотность заряда может быть задана условиями:

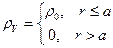. (6)

Здесь . В этом случае мы имеем дело с равномерно заряженным шаром радиуса , за пределами которого зарядов в пространстве нет.

Заряд , находящийся в пространственной области , определяется по формуле:

.

Если 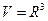, то = .

В подобных случаях для задания объемной плотности заряда удобно использовать функции Хевисайда:

, (7)

, (8)

. (9)

 

Так, объемную плотность заряда (6) можно представить в виде

 

. (10)

 

Так как функции Хевисайда (7)-(9) отличаются лишь на множестве меры нуль, для большинства практических задач безразлично, какая именно из этих функций будет использоваться в выражении (10); во всех случаях заряд , находящийся в пространственной области , будет один и тот же. В любом случае функции Хевисайда дают возможность построить всего лишь математическую модель плотности заряда, ибо они разрывны, а плотность заряда в рамках модели сплошной среды предполагает непрерывность. Позднее мы установим, что функции , , порождают одну и ту же обобщенную функцию.

 

Задача 1. Бесконечная плоская плита ограничена плоскостями и , . Плита равномерно заряжена по объему с плотностью 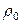. Найдите , используя функцию Хевисайда.

Замечание. В задаче дана математическая модель распределения заряда в конечной пластине, размеры которой существенно превышают расстояние до точки наблюдения.

Решение. При решении данной задачи будем пользоваться функцией . Использовать ли , или - в данном случае неважно.

.

 

Задача 2. Заряд распределен равномерно внутри кубического объема . Выпишите объемную плотность заряда , используя функцию Хевисайда.

Решение.

.

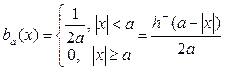, (11)

.

Здесь 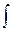- интеграл Лебега по всему пространству.

Замечание. Мы используем функцию Хевисайда только лишь потому, что функция нам пригодится при дальнейшем изложении.

 

Поверхностная плотность заряда. Линейная плотность заряда. На практике встречаются случаи таких заряженных областей, которые следует (можно) моделировать без учета объема, т.е. геометрическими поверхностями или линиями.

Например, заряды на проводящем теле конечных размеров располагаются в поверхностном слое очень малой толщины. Если нас интересует действие заряда на расстояниях, много больших, чем толщина слоя, а не процессы в этом слое, то можно предположить, что весь заряд сосредоточен на поверхности, или, другими словами, этот очень тонкий слой можно считать поверхностью. В этом и аналогичных случаях вводится поверхностная плотность заряда .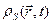

Поверхностная плотность заряда 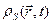определяется так, чтобы величина была равна заряду, находящемуся в момент времени на физически бесконечно малой площади [1], содержащей точку . В этом случае

= , (1)

или

.

Очевидно, что интеграл

(2)

по любой области рассматриваемой поверхности равен полному заряду в этой области в момент времени .

 

Пример. Сфера радиуса равномерно заряжена и имеет заряд . В этом случае , .

 

Аналогично рассматриваются заряженные нити31, для которых вводится линейная плотность заряда.

Линейная плотность заряда определяется так, чтобы величина была равна заряду, находящемуся в момент времени на физически бесконечно малом элементе 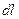длины дуги рассматриваемой нити (элемент 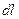содержит точку ). В этом случае

= , (1)

или

.

Очевидно, что интеграл

(2)

по любому сегменту рассматриваемой линии равен полному заряду этого сегмента в момент времени .

 

Следует еще раз отметить, что в реальных условиях распределение заряда в пространстве является объемным. Поверхностное и линейное распределения, а также понятие о точечных зарядах являются идеализацией, использование которых позволяет упростить изучение ЭМ явлений. Для описания идеализированного поверхностного распределения заряда и тока, как и в случае точечных зарядов, можно воспользоваться понятием -функции (которую будем изучать в дальнейшем).

 

Пример. Пусть реальное распределение заряда моделируется его распределением на нити, совпадающей с осью Ох. Пусть

.

Полный заряд нити равен:

= .

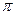Упражнение.

Свяжите плотность реального объемного заряда и плотность модельного поверхностного предельным переходом при , где - толщина слоя зарядов.

Ответ: .

 

Поделиться:

Воспользуйтесь поиском по сайту: