 |
Вычисление определенного интеграла на заданном отрезке с использованием метода правых прямоугольников
|
|
|
|
Оглавление
Задание
Построение графика заданной функции
Поиск корней уравнения  методом половинного деления
методом половинного деления
Определение минимума функции методом перебора
Вычисление определенного интеграла на заданном отрезке с использованием метода правых прямоугольников
Список использованной литературы
Задание
Дана функция вида  .
.
Используя численные методы, необходимо:
1) Построить график функции.
) Определить корни данного уравнения методом половинного деления.
) Определить минимальное значение функции и соответствующее значение аргумента.
) Вычислить значение определенного интеграла методом правых прямоугольников.
Построение графика заданной функции
Построим график функции в программе Microsoft Excel ®. Для этого зададим в табличном виде значения аргумента  на отрезке [-2; 4] и соответствующие им значения функции
на отрезке [-2; 4] и соответствующие им значения функции 
| Значение аргумента x | Значение функции f(x) | Значение аргумента x | Значение функции f(x) | |
| -2,0 | 13,77811 | 1,1 | -3,12426 | |
| -1,9 | 11,98179 | 1,2 | -2,95761 | |
| -1,8 | 10,33929 | 1,3 | -2,76494 | |
| -1,7 | 8,83789 | 1,4 | -2,54681 | |
| -1,6 | 7,46606 | 1,5 | -2,30374 | |
| -1,5 | 6,21338 | 1,6 | -2,03621 | |
| -1,4 | 5,07040 | 1,7 | -1,74463 | |
| -1,3 | 4,02859 | 1,8 | -1,42940 | |
| -1,2 | 3,08023 | 1,9 | -1,09086 | |
| -1,1 | 2,21833 | 2,0 | -0,72933 | |
| -1,0 | 1,43656 | 2,1 | -0,34509 | |
| -0,9 | 0,72921 | 2,2 | 0,06161 | |
| -0,8 | 0,09108 | 2,3 | 0,49052 | |
| -0,7 | -0,48249 | 2,4 | 0,94144 | |
| -0,6 | -0,99576 | 2,5 | 1,41417 | |
| -0,5 | -1,45256 | 2,6 | 1,90855 | |
| -0,4 | -1,85635 | 2,7 | 2,42441 | |
| -0,3 | -2,21028 | 2,8 | 2,96162 | |
| -0,2 | -2,51719 | 2,9 | 3,52005 | |
| -0,1 | -2,77966 | 3,0 | 4,09957 | |
| 0,0 | -3,00000 | 3,1 | 4,70010 | |
| 0,1 | -3,18033 | 3,2 | 5,32152 | |
| 0,2 | -3,32254 | 3,3 | 5,96377 | |
| 0,3 | -3,42836 | 3,4 | 6,62675 | |
| 0,4 | -3,49936 | 3,5 | 7,31039 | |
| 0,5 | -3,53694 | 3,6 | 8,01465 | |
| 0,6 | -3,54238 | 3,7 | 8,73945 | |
| 0,7 | -3,51683 | 3,8 | 9,48474 | |
| 0,8 | -3,46134 | 3,9 | 10,25048 | |
| 0,9 | -3,37686 | 4,0 | 11,03663 | |
| 1,0 | -3,26424 |
|
|
|
Построим на основании полученных табличных данных график исследуемой функции.


Из полученного графика видно, что уравнение  имеет 2 корня: один отрицательный со значением около -0,8, второй - положительный, со значением около 2,2. Минимальное значение функция принимает при
имеет 2 корня: один отрицательный со значением около -0,8, второй - положительный, со значением около 2,2. Минимальное значение функция принимает при  .
.
Поиск корней уравнения  методом половинного деления
методом половинного деления
Зададимся интервалом 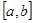 , на котором будем искать корень уравнения
, на котором будем искать корень уравнения  . Очевидно, что признаком наличия на данном интервале корня уравнения есть смена знака значения функции на границах отрезка, или
. Очевидно, что признаком наличия на данном интервале корня уравнения есть смена знака значения функции на границах отрезка, или  . Требуется найти с заданной точностью eps корень этой функции. Выберем середину отрезка
. Требуется найти с заданной точностью eps корень этой функции. Выберем середину отрезка 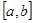 . Если в середине функция имеет тот же знак, что и слева, то примем середину отрезка за новую левую границу, в противном случае - за правую. Повторяем так до тех пор, пока отрезок не станет меньше eps.
. Если в середине функция имеет тот же знак, что и слева, то примем середину отрезка за новую левую границу, в противном случае - за правую. Повторяем так до тех пор, пока отрезок не станет меньше eps.

Dihotomy;;=300;,b,c,eps:Real;:Integer;fx (x:Real): Real;:=sqr(x)+2*exp(-x)-5;;
Writeln ('Нахождение корней функции методом половинного деления');
Repeat('Введите границы отрезка a, b: ');(a,b);fx(a)*fx(b)>0 Then ('На данном отрезке корней нет или их несколько. Попробуйте другие значения')
Endfx(a)*fx(b)<0; ('Введите требуемую точность eps: ');
Readln (eps);:=0;(abs(b-a)>eps) and (st<MaxStep) Do:=st+1;:=(a+b)/2;fx(a)*fx(c)<0b:=ca:=c;;st>MaxStep Writeln ('Отсутствие сходимости. Уточните промежуток')
Else Writeln ('Корень уравнения = ',c:10:6);.
Входные данные a = 0, b =3, eps = 0.000001
Выходные данные Корень уравнения = 2.185197
Определение минимума функции методом перебора
Разобьем отрезок  на
на  отрезков длиной
отрезков длиной 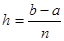 и вычислим значение функции на границах получившихся отрезков. Минимальное среди вычисленных значений и есть искомый минимум функции на данном отрезке.
и вычислим значение функции на границах получившихся отрезков. Минимальное среди вычисленных значений и есть искомый минимум функции на данном отрезке.

Программный код на Turbo Pascal имеет вид
Program Perebor;CRT;,b,h,min,f,xm: Real;,i: Integer;fx (x:Real): Real;:=sqr(x)+2*exp(-x)-5;;
Writeln ('Поиск минимума методом перебора');('Введите границы отрезка a, b: ');(a,b);('Введите количество участков разбиения: ');
|
|
|
Readln (n);:=(b-a)/n;:=a; min:=fx(a);:=1;i<=n Do:=fx(a+i*h);f<min:=a+i*h;:=f;;:=i+1; ('Минимальное значение при x = ',xm:5:2,' равно = ',min:10:5);;.
Пример
Входные данные
a = -1, b =3, n = 10000
Выходные данные
Минимальное значение при x = 0.5672 равно = -3.54406
Вычисление определенного интеграла на заданном отрезке с использованием метода правых прямоугольников
В случае если функция 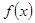 положительна на некотором отрезке
положительна на некотором отрезке  , то значение определенного интеграла этой функции на данном отрезке численно равно площади фигуры, ограниченной сверху графиком функции, а снизу - осью координат
, то значение определенного интеграла этой функции на данном отрезке численно равно площади фигуры, ограниченной сверху графиком функции, а снизу - осью координат  . Разбив отрезок
. Разбив отрезок 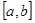 на
на  отрезков длиной
отрезков длиной 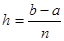 , вычислим площадь фигуры как сумму площадей прямоугольников с основанием
, вычислим площадь фигуры как сумму площадей прямоугольников с основанием  и высотой, равной значению функции в правой границе прямоугольника.
и высотой, равной значению функции в правой границе прямоугольника.
функция интеграл половинный деление

Программа на языке программирования Turbo Pascal имеет вид:
Program RightSquares;;,b,h,s:Real;,i:Integer;fx (x:Real): Real;:=sqr(x)+2*exp(-x)-5;;
Writeln ('Вычисление интеграла методом правых прямоугольников');
Repeat('Введите границы отрезка a, b: ');(a,b);fx(a)*fx(b)<0 Then ('На данном отрезке вычислить интеграл данным методом невозможно')
Endfx(a)*fx(b)>0; ('Введите количество участков разбиения: ');
Readln (n);:=(b-a)/n;:=1;:=0;i<=n Do:=s+h*fx(a+i*h);:=i+1
End;
Writeln ('Значение интеграла на отрезке [',a:5:2,',',b:5:2,'] = ',s:10:5);;.
Пример
Входные данные
a = 2.4, b =4, n = 100
Выходные данные
Значение интеграла на отрезке [ 2.40, 4.00] = 8.95097
Список использованной литературы
1. Учимся программировать: Pascal 7.0, 2-е издание. А.И. Гусева, 1998
. Основы программирования. И.Г. Семакин, А.П. Шестаков, 2001
. Введение в язык ПАСКАЛЬ. В.Г. Абрамов, Н.П. Трифонов, Г.Н. Трифонова, 1998
|
|
|


