 |
Комплексные передаточные функции параллельного контура
|
|
|
|
Возможные режимы установившихся гармонических колебаний в параллельном колебательном контуре
Параллельным колебательным контуром называют цепь, составленную из элементов индуктивности, емкости и сопротивления, соединенных параллельно. Схема контура показана на рисунке 4.
Найдем комплексную проводимость контура:
,
где: 
– активная составляющая проводимости,
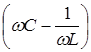– реактивная составляющая проводимости.
Из формулы следует, что в зависимости от соотношения 
и 
в параллельном контуре возможны 3 режима:
1) 
, т.е. 
и 
.
Построим для этого случая векторную диаграмму, положив начальную фазу напряжения на контуре, равной 0 (рис. 5)
Рис. 5
Как видно из векторной диаграммы, ток в контуре опережает напряжение на некоторый угол 
, что является признаком емкостного режима.
Вывод: При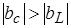 
в параллельном контуре устанавливается емкостной режим колебаний и ток в контуре опережает напряжение.
2) 
т.е. 
и 
.
Построив аналогичным образом векторную диаграмму (рис. 6), убедимся в том, что ток в контуре будет теперь отставать от напряжения 
на некоторый угол 
, что является признаком индуктивного режима.
Рис. 6
Вывод: При в параллельном контуре устанавливается индуктивный режим колебаний, и ток в контуре отстает от напряжения.
3) 
т.е. 
и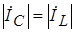 
.
Проводимость контура в этом случае равна активной проводимости G. Контур имеет активный характер, т.е. ток совпадает по фазе с напряжением на контуре и численно равен току через проводимость (рис. 7).
Рис. 7
Такой режим называется резонансом токов и имеет важное практическое значение.
Проведенный анализ показывает, что режим колебаний в параллельном контуре определяется соотношением реактивных проводимостей 
и 
.
|
|
|
Любой из рассмотренных режимов может быть получен несколькими способами: изменением частоты генератора, индуктивности и емкости.
Вывод: Значения режимов ГК в контуре позволяет качественно анализировать процессы, проходящие в контурах, произведя соответствующие инженерные расчёты.
Резонанс токов
1) Резонансная частота
Выше показано, что резонанс токов наступает на частоте, при которой:
откуда 
.
Т.е. резонансная частота равна частоте собственных колебаний контура. Изменение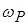 
достигается изменением L или C (чаще).
2) Волновое сопротивление контура
На резонансной частоте,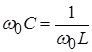 
откуда 
(Ом), т.е. волновое сопротивление контура равно сопротивлению одного из реактивных элементов.
Обычно волновое сопротивление ПК, используемых в электрических цепях, имеет порядок несколько сотен Ом (100 
500).
3) Добротность контура
По определению 
, где, 
следовательно 
.
Т.к. на резонансной частоте численные значения проводимостей 
и 
одинаковые, то добротность можно вычислить по следующей формуле:
, т.о. 
.
4) Резонансное сопротивление контура, токи в ветвях при резонансе
т.к. при резонансе , то 
и 
, т.е. сопротивление контура при резонансе чисто активно и наибольшее по величине.
Действительно, полное сопротивление контура равно:
при 
, 
и 
.
Определим соотношение между током источника и током через реактивный элемент:
, т.е. 
.
Аналогично можно показать, что 
.
Вывод:При резонансе токи в ветвях параллельного КК максимальны и в Q раз больше тока источника. Этим и объясняется название режима – резонанс токов.
При резонансной частоте задающий ток источника замыкается через элемент проводимости контура. Токи же в реактивных элементах контура взаимно компенсируют друг друга относительно внешней цепи контура, или, аналогично, что при резонансной частоте круговой ток замыкается через реактивные элементы контура. При этом 
, а 
наибольшее по величине. При резонансе напряжение на контуре максимально (
). Именно по этому признаку параллельный КК настраивается на резонансную частоту.
|
|
|
Комплексные передаточные функции параллельного контура
Выражения для частотных характеристик параллельно колебательного контура относительно напряжения, можно получить из следующей комплексной передаточной функции:
.
Преобразуем знаменатель 
:
т.о. 
.
Здесь частотно-зависимым является множитель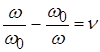 
называемый относительной расстройкой. Произведение 
называют обобщенной расстройкой контура.
C учетом этого: 
.
Из выражения 
получаем
АЧХ: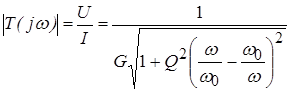 
,
и ФЧХ: 
.
АЧХ называют резонансной характеристикой параллельно колебательного контура. Максимальное значение эта характеристика имеет при резонансной частоте (
), 
.
Резонансную характеристику контура принято нормировать относительно ее максимального значения. Нормированная резонансная характеристика: т.е. отношение амплитуду напряжения при заданной частоте к амплитуде напряжения при резонансе:
.
Нормированная резонансная характеристика есть не что иное, как АЧХ контура относительно тока в элементе активного сопротивления.
.
Найдем приближенное выражение для частотных характеристик колебательного контура со схемой замещения, показанной на рисунке 8.
Она отличается от схемы замещения параллельного колебательного контура тем, что в ней потери в индуктивности реального контура учитываются сопротивлением, включенным последовательно с индуктивностью. Для рассматриваемого контура:
.
В области частот, в которой 
реактивная составляющая сопротивления катушки индуктивности немного превышает по величине активную составляющую её сопротивления, можно пренебречь слагаемым 
в числителе последнего выражения.
Тогда приближенно:
.
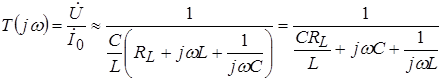Рис. 9
Полученная приближенная формула не отличается от строгой формулы для комплексной передаточной функции параллельного контура с теми же значениями индуктивности L и емкости С и c активной проводимостью:
.
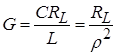Заключение
Рассмотренные режимы установившихся гармонических колебаний в параллельном колебательном контуре позволяют дать физическое объяснение АЧХ и ФЧХ. Частотные характеристики параллельного колебательного контура остаются приближенно верными также и для иных схем замещения реальных колебательных контуров, если интересоваться поведением характеристик в сравнительно узкой полосе частот.
|
|
|
Литература, используемая для подготовки к лекции: Белецкий А.Ф. Теория линейных электрических цепей. – М.: Радио и связь, 1986. (Учебник); Бакалов В.П. и др. Теория электрических цепей. – М.: Радио и связь, 1998. (Учебник); Качанов Н.С. и др. Линейные радиотехнические устройства. М.: Воениздат, 1974. (Учебник); В.П. Попов Основы теории цепей – М.: Высшая школа, 2000.(Учебник)
|
|
|
