 |
Третий уровень (на оценку «5»).
|
|
|
|
Вопросы для размышления
1. Какие из нижеперечисленных правил являются алгоритмами? Ответ обоснуйте:
- орфографические правила;
- правила выполнения арифметических операций;
- правила техники безопасности;
- правила перевода чисел из одной системы счисления в другую.
Задания
1. Составьте алгоритм преобразования слова «информатика» в слово форма.
1.2 Способы записи алгоритма
Существует несколько способов записи алгоритмов.
1. Словесный способ – самый простой и предназначен для исполнения алгоритма человеком. Форма записи произвольная, главное, чтобы она была точной и понятной.
2. Графический способ предполагает использование определенных геометрических фигур, каждая из которых имеет свое функциональное назначение.
3. Запись алгоритма на алгоритмическом языке. Этот способ записи является переходным между человеческим (русским, английским) и машинным языком (языком программирования).
4. Запись алгоритма на языке программирования – единственный способ описания алгоритма, который непосредственно понятен центральному процессору компьютера и с которым он может в дальнейшем работать.
Каждый из последних трех способов мы рассмотрим далее подробнее.
Вопросы для самопроверки:
1. Перечислите способы записи алгоритмов.
2. Какой способ записи самый простой?
3. Опишите графический способ записи.
4. В чем состоит различие между алгоритмическим языком и языком программирования?
1.3 Графическое оформление алгоритма. Создание блок-схем
Графическая форма записи удобна для более наглядного представления различных элементов, из которых состоит алгоритм. При графическом представлении алгоритм изображается в виде определенной геометрической фигуры. Такой способ представления алгоритма называется блок-схемой. Наиболее часто употребляемые геометрические фигуры, входящие в состав блок-схем, приведены на рисунке 1.
|
|
|
Рис. 1. Рис. 2.
Поясним назначение этих блоков.
1. Блоки «начало» и «конец» используются для обозначения начала и конца алгоритма. Внутри обозначающей их фигуры – овала – пишется слово «начало» или «конец».
2. Параллелограмм используется для ввода исходных величин, необходимых для решения задачи. Соответствующие величины указываются внутрипараллелограмма, обозначающего ввод.
3. Вычисления (обработка данных) изображается в виде прямоугольника. Внутри прямоугольника записывается содержание этих вычислений.
4. Проверка определенного условия изображается в виде ромба. Само условие записывается внутри ромба. В результате проверки условия осуществляется выбор одного из двух возможных путей дальнейшего выполнения алгоритма.
5. Иногда алгоритм требует многократного повторения одних и тех же действий. В таких случаях это изображают в виде шестиугольника («конфетки»), в котором определяют количество подобных повторений.
6. Блок вывода («оборванный листок») используется для вывода результата, получившегося в ходе решения задачи. Соответствующие величины указываются внутри фигуры, обозначающей вывод.
ПРИМЕР: Вычислить среднее арифметическое пяти заданных чисел.
Процесс вычисления запишем в виде блок-схемы (рис. 2). После блока, обозначающего начало алгоритма, находится блок ввода исходных данных, к которым относятся значения самих чисел a1, a2 и так далее до самого последнего a5. Следующий, прямоугольный, блок представляет процесс вычисления – нахождение величины S, которая является суммой всех заданных чисел.
Следующий блок также относится к разряду блоков вычислений. В нем производится нахождение величины as – искомого среднего арифметического – сумму пяти чисел надо разделить на их количество (на 5).
|
|
|
В предпоследнем блоке осуществляется вывод полученного результата.
Последний блок представляет собой завершение выполнения алгоритма, о чем говорит соответствующая надпись внутри него.
Правила построения алгоритмов на языке блок-схем:
1. Блок-схема строится сверху вниз.
2. Все входящие в алгоритм блоки соединяются друг с другом прямыми линиями.
3. В любой блок-схеме имеется только один элемент, соответствующий началу алгоритма, и один элемент, соответствующий концу алгоритма.
4. Должен быть хотя бы один путь из начала блок-схемы к любому элементу блок-схемы.
5. Должен быть хотя бы один путь от каждого элемента блок-схемы в конец блок-схемы.
Приведенный способ записи является более строгим, чем словесное описание алгоритма, и не требует большого количества слов. Этот способ почти всегда используется при подготовке решения задачи на компьютере.
Вопросы для самопроверки:
1. Приведите графические элементы блок-схемы алгоритма и опишите их назначение.
2. Опишите правила построения блок-схем.
Вопросы для размышления
1. Зачем нужна блок-схема алгоритма?
1.4 Запись на алгоритмическом языке
Алгоритмический язык – это совокупность определенных знаков, слов, правил, устанавливающих, как с помощью этих знаков описывать алгоритм.
Запись алгоритма на алгоритмическом языке состоит из заголовка и собственно алгоритма (то есть последовательности команд).
В простейшем случае алгоритм на алгоритмическом языке записывается так:
алг имя алгоритма
арг список аргументов (исходные данные) описательная часть
рез список результатов (цель выполнения алгоритма)
нач начало алгоритма
последовательность команд тело алгоритма
кон конец алгоритма
Слова алг, арг, рез, нач, кон называются служебными словами и предназначены для оформления алгоритма. Существуют и другие служебные слова, которые будут рассмотрены далее.
Алгоритм, записанный на алгоритмическом языке, оформляется в соответствии с приведенными ниже правилами.
1. Служебные слова алг, нач и кон пишутся строго одно под другим.
2. Алгоритм должен иметь название. Имя (название) выбирается так, чтобы было понятно, решение какой задачи описывает алгоритм.
|
|
|
3. В строке арг перечисляются имена (названия) всех исходных данных.
4. В строке рез перечисляются имена (названия) тех неизвестных, которые должны быть найдены с помощью этого алгоритма.
5. Команды алгоритма записываются последовательно, одна за другой.
6. Если одна команда не вмещается на одной строке, ее можно перенести на другую строку.
7. Допускается запись нескольких команд на одной строке. В этом случае команды разделяются между собой знаком «точка с запятой» – «;».
Часть алгоритма от строки нач до строки кон называется телом алгоритма, которое представляет собой команды алгоритма. Тело показывает процесс достижения цели алгоритма.
1.5 Алгоритмические структуры
Любой алгоритм может быть реализован в виде комбинации трех базовых алгоритмических конструкций: линейной, ветвления, циклической (рис. 3, 4, 5).
1. Линейным называется алгоритм, в котором все этапы решения задачи выполняются строго последовательно, без пропусков и повторений. Такую алгоритмическую структуру иногда называют «следование». Структура такого алгоритма выглядит как на рисунке 3.
2. Ветвлением называется такая алгоритмическая структура, в которой, в зависимости от истинности условия, выбирается только одно из возможных направлений выполнения алгоритма. Изображение ветвления в виде блок-схемы выглядит как на рисунке 4 (справа представлен неполный вариант ветвления).
Рис. 3. Рис. 4. Рис. 5. 
3. Цикл предусматривает многократное повторение действий (рис. 5).
Циклическим алгоритмом называют алгоритм, в котором набор некоторых действий должен неоднократно выполняться.
Циклические алгоритмы по способу организации выхода из цикла можно разделить на два типа – арифметические (циклы со счетчиком) и итерационные (циклы с условием).
Количество повторений в первых (циклы со счетчиком) заранее известно или может быть легко вычислено.
Количество повторений во вторых (циклы с условием) – заранее неизвестно. Выход из таких циклов осуществляется в зависимости от истинности условия, которое определяет дальнейшую работу цикла: будет ли он выполняться еще раз или будет завершен. Для успешного завершения цикла среди действий внутри цикла должны производиться операции, влияющие на условие. Иначе цикл может стать бесконечным, что приведет к ошибке.
|
|
|
Как видно из рисунков 3, 4, 5, все алгоритмические конструкции имеют общее свойство: один вход и один выход.
Вопросы для самопроверки:
1. Что такое линейный алгоритм? Приведите примеры.
2. Что такое разветвляющийся алгоритм? Приведите примеры.
3. Что такое циклический алгоритм? Приведите примеры.
Вопросы для размышления
1. Чем отличается линейный алгоритм от ветвления?
2. Чем полное ветвление отличается от неполного?
3. В каких случаях используются итерационные циклы?
1.6 Этапы разработки алгоритма
1. Анализ условия задачи.
2. Составление математической модели.
3. На основе математической модели составляют блок-схему алгоритма.
4. Составление алгоритма на алгоритмическом языке и (или) языке программирования.
5. Формальное исполнение алгоритма.
Вопросы для самопроверки:
1. Какие стадии разработки алгоритма вы знаете и в чем их суть?
2. Приведите пример разработки алгоритма по стадиям.
3. Всегда ли результат выполнения одного и того же алгоритма одинаков?
2 Линейные алгоритмы
2.1 Понятие линейного алгоритма
Определение: Линейным называется алгоритм, в котором все этапы решения задачи выполняются строго последовательно, без пропусков и повторений.
Задача 1. Вычислить площадь прямоугольника S. Известно, что его ширина равна а, а длина в 2 раза больше ширины.
Решение.
1. Анализ условия задачи.
Площадь можно найти, перемножив длины сторон. Длина одной стороны известна – ширина а, задаваемая пользователем. Вторую сторону легко найти, зная, что она в 2 раза больше ширины.
Итак, проанализировав условие задачи, делаем вывод, что исходными данными (аргументом), является ширина а прямоугольника, а выходными данными являются длина (вторая сторона) и площадь. Причем вторая сторона – назовем ее b – это промежуточный результат, а площадь – назовем ее S – это искомый результат.
Все эти три объекта являются переменными, поскольку их значения станут известны в процессе выполнения алгоритма: первое будет задано пользователем, а два других будут получены в результате вычислений. Необходимо учесть, что все три переменные это вещественные числа.
2. Составим математическую модель решения нашей задачи. Запишем условие в виде одного предложения – найти площадь прямоугольника.
Наша задача может быть разбита на три основных этапа: ввод исходных данных, этап вычислений и вывод результатов. На первом этапе задается ширина а, на последнем этапе выводится результат – значение площади S.
|
|
|
Этап вычислений детализируем. Сначала вычисляется длина второй стороны – это первая подзадача. Затем, перемножив длины обеих сторон, получим значение площади – искомый результат – это вторая подзадача.
Таким образом, решение данной задачи состоит из двух действий. Используя введенные обозначения, запишем их:
3. Учитывая все выше сказанное, составим блок-схему алгоритма нашей задачи. Она будет выглядеть как на рисунке 1.
4. Запишем алгоритм на алгоритмическом языке.
алг площадь прямоугольника
аргВЕЩ а
резВЕЩ b, S
нач
ввод а
вывод S
кон
|
Рис. 1
2.2 Операторы целочисленного деления DIV и MOD
Во многих языках программирования используют операции, применяемые только для переменных целого типа данных. Это оператор div, позволяющий вычислить целую часть от деления, и оператор mod, позволяющий вычислить остаток от деления. Например, 
, 
. Чаще всего эти операции применяют в задачах о нахождении цифр целого числа.
Задача 2. Дано двузначное число. Найти сумму его цифр.
1. Анализ условия задачи. Дано одно двузначное число. Очевидно, что оно относится к классу целых чисел. Для того чтобы найти сумму цифр, сначала необходимо определить значения каждой цифры данного числа. Итак, делаем вывод, что аргументом является значение самого числа (назовем его Х), промежуточным результатом будут значения цифр этого числа (назовем число десятков А, число единиц В), окончательным результатом будет сумма цифр (назовем ее S).
Все эти объекты являются переменными, поскольку их значения станут известны в процессе выполнения алгоритма: первое будет задано пользователем, а другие будут получены в результате вычислений. Необходимо учесть, что все переменные это целые числа.
2. Составим математическую модель решения нашей задачи. Запишем условие в виде одного предложения – найти сумму цифр двузначного числа. Как и в задаче 10.1 эта задача также может быть разбита на три основных этапа: ввод исходных данных, этап вычислений и вывод результатов.
Детализируем этап вычислений. Понятно, что для получения результата, надо найти значения а) числа единиц; б) числа десятков; в) сумму значений, полученных в пунктах а) и б). Число единиц А найдем, используя операцию вычисления остатка от деления на 10, а число десятков В – с помощью операции вычисления целой части от деления на 10. Очевидно, что сумма S цифр вычисляется простым сложением А и В.
Решение состоит из трех действий. Используя введенные обозначения, запишем их:
.
3. Составим блок-схему алгоритма нашей задачи. Она будет выглядеть как на рисунке 2.
алг сумма цифр
аргЦЕЛ Х
резЦЕЛ А, В, S
нач
ввод Х
вывод S
кон
|
Рис. 2
Алгоритмический язык, также как и любой язык программирования, обладает определенным набором правил, с помощью которых записываются сложные по конструкции выражения.
Правила записи сложных выражений:
1. Аргументы функции записываются в круглых скобках.
2. Знак умножения обязательно прописывается с помощью символа «*». Например, выражение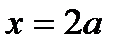 
на алгоритмическом языке следует записывать как 
.
3. Операция деления обозначается с помощью символа «/».
4. Обыкновенная дробь записывается в одну строку. Не допускается запись вида 
. Подобные выражения записываются следующим образом: 
.
5. При наличии в одном выражении нескольких операций они будут выполняться в порядке их приоритета (старшинства).
Пример: Выражение 
следует записывать как: 
Вопросы для самопроверки:
1. Объясните назначение оператора div.
2. Объясните назначение оператора mod.
3. Дайте определение линейного алгоритма.
4. Опишите структуру записи алгоритма на алгоритмическом языке.
Вопросы для размышления:
1. В чем состоит отличие между операторами div, mod и «/»?
2. Что нужно использовать, чтобы изменить приоритет выполнения математических операций?
3. Как называются алгоритмы, в основе которых лежит структура «следование»?
4. Приведите примеры линейных алгоритмов.
Задания
1. Запишите на алгоритмическом языке выражения:
а)  ;
| г) 
| ж)  ;
|
б)  ;
| д)  ;
| з)  ;
|
в)  ;
| е)  ;
| и)  .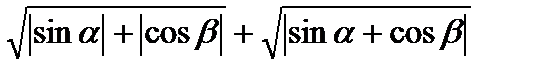
|
2. Запишите на математическом языке выражения, записанные на алгоритмическом языке:
а) a/b*(c+d)-(a-b)/d/c+1;
б) x1+cos(y2-alfa)/2*abs(x4-ln(5)*y5)/sin(x2);
в) (p+q)/(r+s)-p*q/(r*s);
г) (sin(pi*alfa)*sin(pi*alfa))/cos(sqr(beta));
д) a^4/b*sqrt(c+d)-(a-b^3)/sqrt(b).
3. Вычислите значение выражения:
| а) 113 div 7; | г) 238 div 17 - 238 mod 14; |
| б) 113 mod 7; | д) 222 div 2 mod 3; |
| в) 201 div 5 + 201 mod 11; | е) 1363 mod 11 div 3 + 2798 mod 28 div 9. |
4. Разработайте алгоритм (по всем этапам) для решения следующих задач:
а) Вычислить площадь поверхности и объем куба со стороной, равной а.
б) Найдите площадь треугольника со сторонами a, b, c.
в) Дано трехзначное число а. Получить среднее арифметическое его цифр.
г) Написать последовательность для получения числа b, полученного выписыванием в обратном порядке цифр числа а. Если, например, дано число а = 1234, то должно получиться b = 4321.
Задания для выполнения практической работы
Вариант 1.
Первый уровень (на оценку «3»). Дана сторона квадрата а. Найти его периметр по формуле 
и площадь по формуле 
.
Второй уровень (на оценку «4»). Дано трехзначное число. Найти сумму квадратов его цифр.
Третий уровень (на оценку «5»). Дано четырехзначное число. Найти сумму S1 двух первых и сумму S2 двух последних его цифр.
Вариант 2.
Первый уровень (на оценку «3»).
Дан диаметр окружности d. Найти ее длину по формуле L = π∙d. В качестве значения π использовать 3.14.
Второй уровень(на оценку «4»). Дано трехзначное число. Найти сумму кубов его цифр.
Третий уровень (на оценку «5»)..
Дано пятизначное число. Найти произведение трех средних его цифр.
Вариант 3.
Первый уровень (на оценку «3»).
Найти длину окружности L и площадь круга S заданного радиуса R по формулам L = 2∙π∙R, S = π∙R2 . В качестве значения π использовать 3.14.
Второй уровень (на оценку «4»). Дано трехзначное число. Найти сумму квадратов первой и последней его цифр и вычесть квадрат второй цифры.
Третий уровень (на оценку «5»).
Дано четырехзначное число. Найти сумму S1 двух крайних и сумму S2 двух средних цифр.
Вариант 4.
Первый уровень (на оценку «3»).
Вычислите значение функции 
при заданных значениях a, b, h.
Второй уровень (на оценку «4»). Дано трехзначное число. Найти сумму кубов первой и последней его цифр и вычесть куб второй цифры.
Третий уровень (на оценку «5»).
Дано четырехзначное число. Найти разность R1 между двумя первыми и разность R2 между двумя последними его цифрами.
3 Алгоритм ветвления (условный алгоритм)
Определение: Алгоритмом ветвления (условным алгоритмом) называется такая алгоритмическая структура, в которой, в зависимости от истинности некоторого выражения (условия), производится выбор одного из двух направлений выполнения алгоритма, называемых ветвями.
На языке блок-схем ветвление может изображаться в виде как на рисунке:
На алгоритмическом языке команда ветвления записывается следующим образом:
| ЕСЛИ условие ТО действие1 ИНАЧЕ действие2 ВСЕ | В зависимости от итога проверки условия выполняется только одно из двух действий, входящих в команду ветвления. Если условие соблюдено, то следует выполнять действие1, если нет – действие2. |
Эта форма записи называется полной. Существует еще и оператор ветвления и в неполной форме:
| ЕСЛИ условие ТО действие ВСЕ | При этом если условие истинно, необходимо выполнить действие, следующее в записи алгоритма за служебным словом ТО, в противном случае надо перейти к выполнению команды, следующей ЗА командой ветвления (после служебного слова ВСЕ). |
Рассмотрим пример.
Задача 3. Даны два числа А и В. Найти наибольшее из них.
1. Анализируем условие.Что дано в задаче? а) Первое число А. Это переменная, ее задает пользователь в начале алгоритма. б) Второе число В. Тоже переменная определяется в начале алгоритма. Что является результатом в этой задаче? Максимальное из этих двух заданных чисел. Обозначим эту переменную через Max. Все эти переменные относятся к классу действительных чисел.
2. Математическая модель. Запишем условие в виде одного предложения – найти максимальное из двух заданных чисел.
Что необходимо сделать для этого? Для этого надо сравнить их и выбрать наибольшее из них следующим образом: если первое число больше второго, то максимальное – это первое число, если второе число больше первого, то максимальное – это второе число.
Заметим, что эти две ситуации взаимно противоположные: либо первое число больше, либо второе. Поэтому условно можно считать, что один случай соответствует слову «да», тогда другой случай соответствует слову «нет». Может быть еще случай, когда эти числа равны между собой. Тогда оба они равны максимальному значению.
Итак, алгоритм решения задачи состоит из этапа ввода чисел, этапа сравнения этих чисел и, наконец, этапа вывода максимального числа.
Этап сравнения этих чисел описывается так, как было сказано выше, если A больше, чем B, то Мах равен A, в другом случае (если B больше, чем A) Мах равен B. Запишем «русские слова» на математическом языке – языком формул:
Если A>B, то Мах=А, иначе Мах=В.
3. Блок-схема алгоритма нашей задачи будет выглядеть как на рисунке 3.
4. Запишем алгоритм на алгоритмическом языке.
| АЛГ БИД АРГВЕЩ А, В РЕЗВЕЩ Мах НАЧ ввод А, В ЕСЛИ A > B ТО Мах:= A ИНАЧЕ Мах:= В ВСЕ вывод Мах КОН |
Рис. 3
Вопросы для самопроверки:
1. Что такое разветвляющийся алгоритм? Приведите примеры.
2. Как записывается полная форма алгоритма ветвления? Приведите примеры.
3. Как записывается неполная форма разветвляющегося алгоритма? Приведите примеры.
4. Напишите знаки логических операций, используемые в условии алгоритма ветвления.
Вопросы для размышления
1. Как в блок-схеме алгоритма записывается условие?
2. Зачем нужна блок-схема алгоритма?
3. Для чего используются ветвления?
4. Приведите примеры условных алгоритмов.
Задания
1. Какое значение будет принимать переменная х, после выполнения фрагмента алгоритма:
а) f:= 25; d:= 37;
ЕСЛИ f <= d ТО x:= f ИНАЧЕ x:= d ВСЕ;
б) a:= 13; b:= 14;
ЕСЛИ a > b ТО x:= a * b ИНАЧЕ x:= a – b ВСЕ;
в) a:= 75; b:= 74; c:= 73
ЕСЛИ a > b ТО x:= a + b ИНАЧЕ a:= b + c; x:= a – 3 * b ВСЕ;
г) a:= 55; b:= 58; c:= 52
ЕСЛИ (a>b) И (b>c) ТО x:= 2 * a + b + c ИНАЧЕ x:= a – b + c ВСЕ;
д) a:= 37; b:= 33; c:= 36
ЕСЛИ (a<b) ИЛИ (a>c) ТО x:= 4 * a – a * b ИНАЧЕ x:= 2 * (a – b) ВСЕ.
2. Дана блок-схема. Напишите алгоритм на алгоритмическом языке по данной блок-схеме.
 а)
|  б)
|
в)
|  г)
|
3. Разработайте алгоритм (по всем этапам) для решения следующих задач:
3.1. Найти наименьшее среди трех заданных чисел.
3.2. Решить квадратное уравнение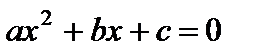 
.
3.3. Вычислить значение функции 
при заданном значении аргумента х.
3.4. Составить алгоритм решения линейного уравнения 
.
3.5. Вычислить значение функции у при заданном значении аргумента х:
Задания для выполнения практической работы
Вариант 1
Первый уровень (на оценку «3»). Разработать алгоритм для решения задачи.
Дано целое число. Если оно является положительным, то прибавить к нему 1; в противном случае не изменять его. Вывести полученное число.
Второй уровень (на оценку «4»).
Разработать алгоритм для вычисления значения функции.
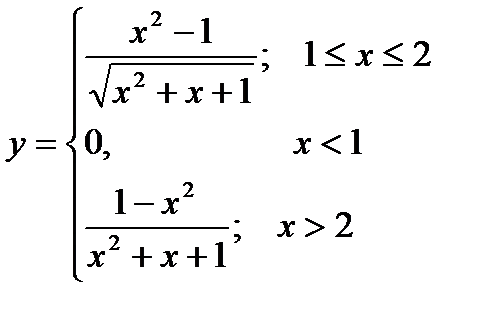
Третий уровень (на оценку «5»).
Разработать алгоритм для нахождения наименьшего: 
Вариант 2
Первый уровень (на оценку «3»). Разработать алгоритм для решения задачи.
Дано целое число. Если оно является положительным, то прибавить к нему 1; в противном случае вычесть из него 2. Вывести полученное число.
Второй уровень (на оценку «4»).
Разработать алгоритм для вычисления значения функции.
Третий уровень (на оценку «5»).
Разработать алгоритм для нахождения наибольшего: 
Вариант 3
Первый уровень (на оценку «3»). Разработать алгоритм для решения задачи.
Даны два числа. Вывести порядковый номер меньшего из них.
Второй уровень (на оценку «4»).
Разработать алгоритм для вычисления значения функции.
Третий уровень (на оценку «5»).
Разработать алгоритм для нахождения наибольшего: 
4 Циклические алгоритмы
4.1 Алгоритмы цикла типа «ДЛЯ» (цикл со счетчиком)
Определение: Цикл, в котором количество повторений действий известно заранее, называется циклом со счетчиком ( или параметром ).
Вспомним, как этот тип цикла оформляется в идее блок-схемы:
На алгоритмическом языке оператор цикла со счетчиком имеет следующую форму записи:
| ДЛЯ I:= I_НАЧ ДО I_КОН НЦ действия (тело цикла) КЦ | 
|
I – управляющая переменная цикла, так называемый счетчик цикла, значение которого меняется от начального (I_НАЧ) до конечного (I_КОН). После того как переменная-счетчик цикла примет конечное значение, тело цикла выполнится в последний раз и цикл будет завершен. Переменная-счетчик должна быть целого типа.
I_НАЧ и I_КОН – это начальное и конечное значения счетчика цикла. Оба значения должны быть того же типа, что и счетчик цикла, то есть целого.
<тело_цикла> или <действия> – обычно в качестве тела цикла выступают те команды, которые используются для описания повторяющихся действий.
Правила записи оператора цикла со счетчиком:
1. Определить параметр цикла (изменяющуюся величину, связанную с повторяющимися действиями) и дать ей имя.
2. Определить начальное и конечное значения параметра цикла.
3. Определить повторяющиеся действия и записать их.
Работа цикла «ДЛЯ».
Сначала параметру цикла (счетчику) присваивается начальное значение, затем проверяется выполнение условия: значение параметра цикла меньше или равно конечному значению. Если условие истинно, то выполняются команды, идущие после НЦ, и значение параметра цикла автоматически увеличиваются на единицу. Далее снова проверяется выполнение условия: значение параметра цикла меньше или равно конечному значению. И если условие верно, то снова выполняются команды, идущие после НЦ. Этот процесс продолжается до тех пор, пока условие не станет ложным. В случае, когда условие является ложным на первом шаге, оператор вообще не выполняется ни разу.
Задача 4. Алгоритм нахождения суммы чисел
Давайте определим, как найти сумму чисел? Надо взять первые два числа и сложить их, потом к полученной сумме прибавить следующее число и так далее пока не сложим все числа.
Заметим, что всегда повторяется одно и то же действие: к старой сумме прибавляется следующее число.
Только самое первое действие немного отличается. Мы складываем два числа. Было бы хорошо, если бы все действия были бы одинаковыми, тогда задачу можно было бы решить с помощью цикла. Этого можно добиться, если задать начальную сумму, равной нулю. (Символично это будет первое число, и оно не изменит значение суммы). А затем к ней прибавим первое число, к полученной сумме второе и так далее.
Мы получили алгоритм нахождения суммы чисел. Этот алгоритм можно использовать во многих задачах. Его необходимо понять и запомнить.
Обозначим сумму S, а число. Тогда алгоритм нахождения суммы 5 чисел будет иметь следующий вид:
1) Параметр цикла: счетчик, который считает, сколько чисел уже введено и прибавлено к сумме. Пусть его имя будет I.
2) Начальное значение параметра цикла равно 1, конечное значение параметра цикла равно 5.
3) Повторяющиеся действия:
| Ввод X | {на каждом новом шаге прибавления узнаем значение следующего числа} |
| S:= S + X | {новое значение суммы (S, стоящее слева) получается путем прибавления к старому значению (S, стоящее справа) только что полученное число X} |
Надо иметь ввиду, что начальное значение суммы S:= 0.
1. Анализируем условие.Что дано в задаче? – числа X. Это переменная вещественного типа. Что является результатом в этой задаче? – Сумма S, которая тоже является переменной вещественного типа. Есть еще промежуточный результат. Это счетчик I – переменная целого типа.
Так как есть действия, которые повторяются известное количество раз, то для решения задачи необходимо использовать цикл со счетчиком (цикл типа «ДЛЯ»).
2. Математическая модель. Здесь опишем формальную схему работы цикла со счетчиком
1. S:= 0
2. (действия цикла)
2.1. Параметр цикла – переменная I.
2.2. Начальное значение I равно 1, конечное значение I равно 5.
2.3. Повторяющиеся действия:
Ввод X
S:= S + X
3. После завершения работы цикла:
Вывод S
3. Блок-схема алгоритма нашей задачи будет выглядеть как на рисунке 4.
4. Запишем алгоритм на алгоритмическом языке.
| АЛГ сумма5 АРГВЕЩ X РЕЗВЕЩ S, ЦЕЛ I НАЧ S:= 0 ДЛЯ I:= 1 ДО 5 НЦ Ввод X S:= S + X КЦ Вывод S КОН |
 Рис. 4.
|
Задача 5: Таблица значений функции
Давайте решим следующую задачу. Получить таблицу значений функции 
на отрезке [a, b] с шагом h.
1. Анализ условия. Дано: константы a и b, обозначающие концы отрезка функции, а также шаг h. Результат: аргумент и значение функции X и Y – переменные вещественного типа.
2. Математическая модель. Так как функция вычисляется несколько раз по одной формуле, то используем цикл со счетчиком. Для этого необходимо знать, сколько именно раз вычисляется функция. Для подсчета этого количества используем формулу, известную из математики: 
. Понятно, что может получиться нецелое число, поэтому его округляют в меньшую сторону и прибавляют единицу: 
. Если известны значения всех переменных, то значение n можно вычислить с помощью карандаша и бумаги. Но можно обойтись командами ввода переменных a, b и h и последующей записью приведенной формулы для n.
Например, если была поставлена задача получить таблицу значений функции на отрезке [-2, 2] с шагом 0,5, тогда a=-2,0, b=2,0 и h=0,5, а
Запишем математическую модель с помощью формул и математических соотношений.
1. ввод a, b и h {введем значения концов отрезка и шаг}
2. {подсчитаем количество значений}
3. Х:= а {придадим Х начальное значение, равное правому концу отрезка}
4. (вычисление и вывод значений аргумента и функции)
4.1. Параметр цикла – переменная I, означает, какое по счету значение аргумента вычисляется.
4.2. Начальное значение I равно 1, конечное значение I равно n.
4.3. Повторяющиеся действия:
X:= X + h {Вычислить следующее значение аргумента X }
Y:= 2 * X + 5 {значение функции, соответствующее аргументу}
Вывод X, Y
3. Блок-схема алгоритма нашей задачи будет выглядеть как на рис. 6.
4. Запишем алгоритм на алгоритмическом языке.
| АЛГ таблица функции
АРГ
РЕЗВЕЩ X, Y
ЦЕЛ I
НАЧ
ввод a, b, h
Х:= а
ДЛЯ I:= 1 ДО n
НЦ
X:= X + h
Y:= 2 * X + 5
Вывод X, Y
КЦ
КОН
|
Рис. 5
|
Вопросы для самопроверки:
1. Какая форма организации действий называется циклом?
2. Какие данные необходимы для организации цикла?
3. Когда применяется цикл «ДЛЯ»?
4. Что такое управляющая переменная цикла?
5. Что вы знаете о шаге в цикле?
6. Что такое тело цикла?
Вопросы для размышления:
1. Какой тип алгоритмической структуры необходимо применить, если:
-последовательность команд должна быть выполнена определенное количество раз;
-последовательность команд выполняется или не выполняется в зависимости от условия;
-последовательность команд должна быть обязательно выполнена хотя бы один раз и должна повторяться до тех пор, пока условие справедливо?
2. Напишите циклический алгоритм и укажите в нем тело цикла.
Задания
1. Какое значение будет принимать переменная Y после выполнения фрагмента алгоритма:
| а) Y:= 0 ДЛЯ K:= 1 ДО 9 НЦ Y:= Y + K КЦ | в) Y:= 1 ДЛЯ K:= 1 ДО 5 НЦ Y:= Y * Х КЦ |
| б) Y:= 0 ДЛЯ K:= 1 ДО 9 НЦ Y:= Y + Х КЦ | г) X:= 0; Y:= 1 ДЛЯ K:= 1 ДО 5 НЦ Х:= Х + 2; Y:= Y * Х КЦ |
д)
|
е)
|
ж)
| 
з)
|
2. Дана блок-схема. Напишите алгоритм на алгоритмическом языке по данной блок-схеме.
 а)
| б)
|
3. Разработайте алгоритм (по всем этапам) для решения следующих задач:
3.1. Десять чисел вводятся по одному. Вычислить их среднее арифметическое.
3.2. Двадцать чисел вводятся по одному. Вычислить прои
|
|
|
