 |
Краткий обзор предыдущих результатов
|
|
|
|
Введение
Общие сведенья по клеточным автоматам
Клеточный автомат – это математический объект с дискретным пространством и временем. Каждое положение в пространстве представлено отдельной клеткой, а каждый момент времени – дискретным шагом или поколением. Состояние каждой клетки определяется некоторыми правилами взаимодействия. Эти правила предписывают изменения состояния каждой клетки в следующем такте времени в ответ на текущее состояние соседних клеток.
Общие правила построения клеточных автоматов:
1. Состояние клеток дискретно (0 или 1, но могут быть автоматы и с большим числом состояний).
2. Соседями является ограниченное число клеток.
3. Правила, задающие динамику развития клеточного автомата, имеют некоторую функциональную форму.
4. Клеточный автомат является тактируемой системой, т.е. смена клеток происходит одновременно.
Условные обозначения
| V(G) | Множество вершин графа G |
| E(G) | Множество ребер графа G |
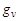
| Поддерево g с корнем v |
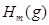
| Множество вершин полного корневого поддерева g с корнем v дерева G, находящихся на m-том ярусе, относительно корня v. |
D(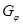 ) )
| Множество висячих вершин графа 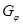
|
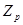
| Поле вычетов по mod p (p – простое), т.е. {1,2,..,p-1} |
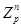
| 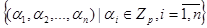
|
Некоторые стандартные обозначения векторов из 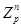
| (0,0,0,…,0)= | en | (1,0,1,1,0,1,…,0,1)= | rn для n=2k+1 |
| (1,0,0,…,0)= | dn | (1,1,0,1,1,0,…,1,1)= | sn для n=3k+2 |
Цели:
1. Исследовать структуру графа 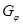 :
:
· определить количество и высоту деревьев, описать их структуру;
· определить количество и длину циклов графа 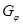 ;
;
· описать множество висячих вершин графа 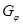 .
.
2. Рассмотреть те же вопросы для случая произвольного линейного оператора.
§2 Структура графа состояний для линейного оператора над Zp
|
|
|
Введение
Рассмотрим множество 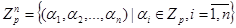 и линейный оператор
и линейный оператор 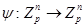 такое, что y – линейный оператор над полем Zp, в частности, этот оператор может задавать изменение состояния некоторого одномерного клеточного автомата с p состояниями.
такое, что y – линейный оператор над полем Zp, в частности, этот оператор может задавать изменение состояния некоторого одномерного клеточного автомата с p состояниями.
Будем рассматривать граф состояний  , для которого
, для которого 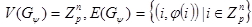 . Основной целью исследования является изучение структуры графа
. Основной целью исследования является изучение структуры графа  .
.
Одним из важных свойств оператора y, которое будет использоваться в дальнейшем, является его аддитивность:

Для исследования структуры графа Gy рассмотрим следующую нумерацию вершин нулевого дерева (см. рис. 2.1).
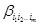 – вершина, находящаяся на m ярусе, при этом она входит в
– вершина, находящаяся на m ярусе, при этом она входит в 
(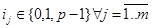 ), смысл этих обозначений станет ясным позже. Важно то, что в этих обозначениях в вершину
), смысл этих обозначений станет ясным позже. Важно то, что в этих обозначениях в вершину 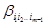 входят
входят 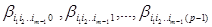 , при этом вершины
, при этом вершины  входят в
входят в 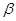 (в нашем случае.
(в нашем случае.
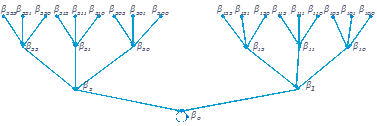
Рис. 2.1
Теорема 2.1
Пусть задана цепь: 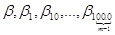 тогда
тогда  .
.
Доказательство:
Воспользуемся методом математической индукции.
База m=1:

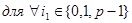 , действительно
, действительно  причем
причем 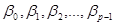 различные вершины, ч.т.д.
различные вершины, ч.т.д.
Пусть теорема верна для m = l-1, т.е  .
.
Докажем, что 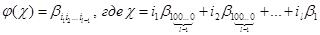 Тем, самым, по построению
Тем, самым, по построению 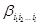 , мы покажем, что
, мы покажем, что 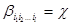 .
.
Действительно, в силу линейности 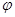 :
:

Теорема 2.1 доказана.
Назовем дерево с корнем en = (0,0,…,0) – «нулевым» деревом, тогда для него верна следующая теорема.
Теорема 2.2
«Нулевое» дерево – p-нарное дерево с точностью до петли в корне (0,0..,0).
Доказательство:
По теореме 2.1 единственная цепь из висячей вершины в (0,0,..0) однозначным образом определяет все элементы дерева (различность определяемых вершин очевидна, и следует из простоты p).
Теорема 2.3
Каждое дерево притягиваемого каждой точкой каждого цикла графа Gy изоморфно нулевому» дереву.
Доказательство:
Для любых последовательностей k и l, находящихся на одном ярусе какого-то дерева, для которых выполняется условие:

верно равенство:
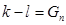 ,
,
где 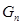 ―одна из последовательностей «нулевого» дерева на n-ном ярусе (сумма в поле
―одна из последовательностей «нулевого» дерева на n-ном ярусе (сумма в поле 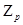 ) (Следует из теоремы 2.1).
) (Следует из теоремы 2.1).
|
|
|
Используя полученное соотношение можно достроить любое дерево до дерева изоморфного «нулевому».
ACS-автомат
Постановка задачи
В данной работе рассматривается клеточный автомат (одномерный), функционирование которого осуществляется по следующим правилам:
Дана полоска 1  n (сам автомат), все клетки, которой находятся в состояниях «0» и «1». Изменение состояния клетки определяется следующим образом: данная клетка переходит в состояние «1», если её соседи находятся в разных состояниях, и в «0»,если её соседи находятся в одинаковых состояниях. Клетки, находящиеся по краям переходят в то же состояние, которое было у единственной соседней клетки в предыдущий момент времени.
n (сам автомат), все клетки, которой находятся в состояниях «0» и «1». Изменение состояния клетки определяется следующим образом: данная клетка переходит в состояние «1», если её соседи находятся в разных состояниях, и в «0»,если её соседи находятся в одинаковых состояниях. Клетки, находящиеся по краям переходят в то же состояние, которое было у единственной соседней клетки в предыдущий момент времени.
По полоске длины n будем определять вектор 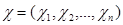 , где
, где 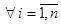 :
:
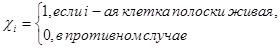
Рассмотрим множество 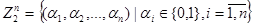 и отображение
и отображение 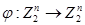 такое, что
такое, что

(здесь и ниже 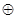 – операция сложения по mod p=2, т.е. операция сложения в поле Z2).
– операция сложения по mod p=2, т.е. операция сложения в поле Z2).
Будем рассматривать граф состояний 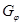 , для которого
, для которого 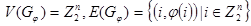 . Основной целью исследования является изучение структуры графа
. Основной целью исследования является изучение структуры графа 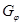 .
.
Для начала рассмотрим некоторые определения и обозначения, которые будут использоваться в дальнейшем в работе:
· Ориентированное дерево — это ориентированный граф без циклов, в котором из каждой вершины, кроме одной, называемой корнем ориентированного дерева, выходит ровно одно ребро (более подробно структуры дерева будет определена позже).
· m-й ярус – множество вершин дерева, находящихся на расстоянии m от корня.
· Частичный порядок на вершинах: 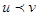 , если вершины u и v различны и вершина u лежит на единственном элементарном пути, соединяющем вершиной v с корнем дерева.
, если вершины u и v различны и вершина u лежит на единственном элементарном пути, соединяющем вершиной v с корнем дерева.
· Корневое поддерево с корнем v — подграф 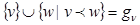 .
.
· Множество 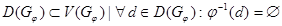 назовем множеством висячих вершин графа
назовем множеством висячих вершин графа 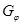 .
.
Краткий обзор предыдущих результатов
В прошлом году на ряде конференций (см. Используемые источники) была представлена работа по клеточным автоматам, в которой был исследован частный случай линейного оператора и найдены высоты деревьев для последовательностей, состоящих из 2n-1 элементов. В ней были представлены следующие утверждения, которые будут использоваться в дальнейшем:
Утверждение 3.2.1
 .
.
Утверждение 3.2.2
|
|
|
1. 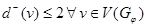 ;
;
2. 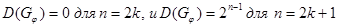 , причем
, причем 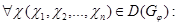
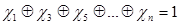
3.  ;
;
4. 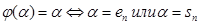 .
.
Утверждение 3.2.3
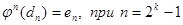 ;
; 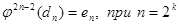 и
и 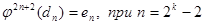 .
.
Предисловие
В параграфе будет рассказано о свойствах графа состояний оператора j, а именно будет описана его структура.
§3.3 Структура Gj при p=2
Исследование структуры
Пользуясь утверждением 3.2.2, мы получаем, что среди всех последовательностей можно выделить следующие:
1. которые невозможно получить не из каких других, например: (1,0,0) (они будут образовывать висячие вершины графа);
2. которые, спустя несколько итераций возвращаются в начальное положение, например:
(1,0,0,0) ® (0,1,0,0) ® (1,0,1,0) ® (0,0,0,1) ® (0,0,1,0) ® (0,1,0,1) ® (1,0,0,0)
(такие последовательности в графе будут соответствовать вершинам цикла)
Используя утверждение 3.2.2, можно сделать вывод:
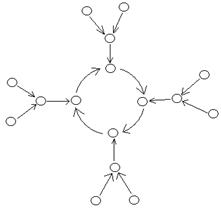
Теорема 3.3.1.1
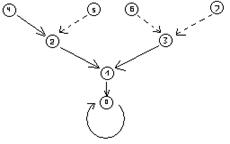
Каждая компонента связности графа 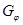 является циклом (возможно длины 1), каждый элемент которого притягивает дерево (т.е. является корнем ориентированного дерева) (см. рис. 3.2.1).
является циклом (возможно длины 1), каждый элемент которого притягивает дерево (т.е. является корнем ориентированного дерева) (см. рис. 3.2.1).
Наша основная задача определить длины циклов и высоты деревьев, описать их структуру и найти их количество.
|
Теорема 3.3.1.2
Для любых последовательностей k и l, находящихся на одном ярусе какого-то дерева, для которых выполняется условие: 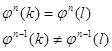 верно равенство:
верно равенство:
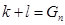 , где
, где 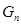 ―одна из последовательностей «нулевого» дерева на n-ном ярусе.
―одна из последовательностей «нулевого» дерева на n-ном ярусе.
Более точно это можно сформулировать так:

Рис. 3.2.2
Для любого «полного» корневого поддерева g с корнем v дерева G (с корнем в 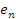 ):
): 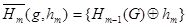 , где
, где 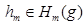 и
и  – подмножество
– подмножество 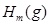 такое, что:
такое, что: 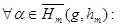
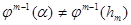 , при этом
, при этом 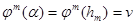 (см. рис. 3.2.2).
(см. рис. 3.2.2).
Доказательство
Воспользуемся методом математической индукции:
1. m = 1:
Пусть  , тогда
, тогда 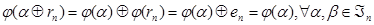 . Тогда, учитывая утверждение 1.1,
. Тогда, учитывая утверждение 1.1,  и
и 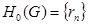 , получим требуемое.
, получим требуемое.
2. Пусть утверждение леммы верно для m = k, тогда:
3. Докажем теорему для m = k+1.
Мы имеем: 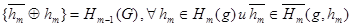 , тогда:
, тогда:
Если 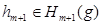 и
и 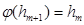 , то
, то  :
:
Из утверждения 3.2.1:
 , но
, но 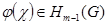 , т.е.
, т.е. 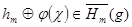 , откуда
, откуда  , ч.т.д.
, ч.т.д.
Теорема 3.3.1.3
«Нулевое» дерево ― бинарное дерево с точностью до петли в корне en.
Доказательство:
|
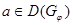 и,
и,  тогда мы можем достроить его, пользуясь теоремой 3.3.1.2 до бинарного дерева с точностью до петли в корне en (см. рис. 3.3.3) Заметим, что n+1-го яруса быть не может т.к. тогда мы достраиваем этот ярус и получаем
тогда мы можем достроить его, пользуясь теоремой 3.3.1.2 до бинарного дерева с точностью до петли в корне en (см. рис. 3.3.3) Заметим, что n+1-го яруса быть не может т.к. тогда мы достраиваем этот ярус и получаем 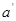 такое, что
такое, что 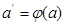 но
но 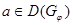 – противоречие.
– противоречие.|
|
|
Теорема 3.3.1.4
Все деревья (в том числе и примыкающие к каждой вершине произвольного цикла) будут иметь столько ярусов, сколько и «нулевое», причем будут иметь такую же структуру.
Более точно: дерево, притягиваемое каждой точкой каждого цикла графа состояний, изоморфно дереву, притягиваемому точкой en.
Доказательство:
Предположим «нулевое» дерево состоит из n ярусов тогда:
1. Если наше дерево состоит менее чем из n ярусов, то, пользуясь теоремой 3.3.1.2, мы восстанавливаем его до дерева изоморфного «нулевому».
2. Если дерево имеет m ярусов, где n<m тогда 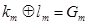 , получается, что «нулевое» дерево состоит из m ярусов Ї противоречие.
, получается, что «нулевое» дерево состоит из m ярусов Ї противоречие.
|
|
|
12 |


