Главная | Обратная связь | Поможем написать вашу работу!

Метод разделяй и властвуй при построении алгоритмов, пример алгоритма

Макс

Асимптотическая оценка алгоритма

является наглядной характеристикой эффективности алгоритма, а также позволяет сравнивать производительность различных алгоритмов.

{Асимптотически положительной называется такая функция, которая является положительной при любых достаточно больших n).

Для всех n≥n₀функция f (n) равна функции g (n) с точностью до

постоянного множителя. Говорят, что функция g(n) является асимптотически

точной оценкой функции f (n).

Обозначения:

В 0-обозначениях функция асимптотически ограничивается сверху и снизу.

Если же достаточно определить только асимптотическую верхнюю границу,

используются О-обозначения. в Ω-обозначениях дается ее асимптотическая нижняя граница.

Методика оценки не рекурсивных алгоритмов

Время работы алгоритма — это сумма промежутков времени, необходимых для

выполнения каждой входящей в его состав исполняемой инструкции. Если выполнение инструкции длится в течение времени и она повторяется в алгоритме n раз, то ее вклад в полное время работы алгоритма равно n.

Даже если размер входных данных является фиксированной величиной, время

работы алгоритма может зависеть от степени упорядоченности сортируемых ве-

величин, которой они обладали до ввода.

Рекурсивные алгоритмы, построение асимптотической оценки

Многие полезные алгоритмы имеют рекурсивную структуру: для решения дан-

данной задачи они рекурсивно вызывают сами себя один или несколько раз, чтобы

решить вспомогательную задачу, имеющую непосредственное отношение к по-

поставленной задаче. Такие алгоритмы зачастую разрабатываются с помощью

метода декомпозиции, или разбиения: сложная задача разбивается на несколько более простых, которые подобны исходной задаче, но имеют меньший объем; далее эти вспомогательные задачи решаются рекурсивным методом, после чего полученные решения комбинируются с целью получить решение исходной задачи.

Парадигма, лежащая в основе метода декомпозиции "разделяй и властвуй", на

каждом уровне рекурсии включает в себя три этапа.

Разделение задачи на несколько подзадач.

Покорение — рекурсивное решение этих подзадач. Когда объем подзадачи доста-

достаточно мал, выделенные подзадачи решаются непосредственно.

Комбинирование решения исходной задачи из решений вспомогательных задач.

Если алгоритм рекурсивно обращается к самому себе, время его работы часто

описывается с помощью рекуррентного уравнения, или рекуррентного соотношения, в котором полное время, требуемое для решения всей задачи с объемом ввода n, выражается через время решения вспомогательных подзадач. Затем данное рекуррентное уравнение решается с помощью определенных математических методов, и устанавливаются границы производительности алгоритма.

Метод получения асмптот оценки по рекур отношению:

Интерация – рассматриваем формулу в сумму элементов которые вычисляются на основе формулы n элементов

Основная теорема для рекурсивных алгоритмов

Теорема является своего рода "сборником рецептов", по которым строятся решения рекуррентных соотношений вида

где а≥1иb>1 — константы, а / (n) — асимптотически положительная функция.

Чтобы научиться пользоваться этим методом, необходимо запомнить три случая,

что значительно облегчает решение многих рекуррентных соотношений, а часто

это можно сделать даже в уме.

Метод разделяй и властвуй при построении алгоритмов, пример алгоритма

Если алгоритм рекурсивно обращается к самому себе, время его работы часто

Получение рекуррентного соотношения для времени работы алгоритма, основанного на принципе "разделяй и властвуй", базируется на трех этапах, соответствующих парадигме этого принципа. Обозначим через T (n) время решения задачи, размер которой равен п. Если размер задачи достаточно мал, скажем, n ≤ c, где с — некоторая заранее известная константа, то задача решается непосредственно в течение определенного фиксированного времени, которое мы обозначим через . Предположим, что наша задача делится на а подзадач, объем каждой из которых равен 1/Ь от объема исходной задачи.

Если разбиение задачи на вспомогательные подзадачи происходит в течение времени D (n), а объединение решений подзадач в решение исходной задачи — в течение времени С (n), то мы получим такое рекуррентное соотношение:

пример алгоритма сортировка слиянием

public void merge(int []arr, long left, long middle, long right) {

// Слияние упорядоченных частей массива в буфер temp

// с дальнейшим переносом содержимого temp в a[left]...a[right]

// текущая позиция чтения из первой последовательности a[left]...a[middle]

long pos1=left;

// текущая позиция чтения из второй последовательности a[middle+1]...a[right]

long pos2=middle+1;

// текущая позиция записи в temp

long pos3=0;

int[] temp = new int[right-left+1];

// идет слияние, пока есть хоть один элемент в каждой последовательности

while (pos1 <= middle && pos2 <= right)

{

if (arr[pos1] < arr[pos2])

temp[pos3++] = arr[pos1++];

else

temp[pos3++] = arr[pos2++];

}

// одна последовательность закончилась -

// копировать остаток другой в конец буфера

while (pos2 <= right) // пока вторая последовательность непуста

temp[pos3++] = arr[pos2++];

while (pos1 <= middle) // пока первая последовательность непуста

temp[pos3++] = arr[pos1++];

// скопировать буфер temp в a[lb]...a[ub]

for (pos3 = 0; pos3 < right - left + 1; pos3++)

arr[left + pos3] = temp[pos3];

}

//a - сортируемый массив, его левая граница left, правая граница right

void mergeSort(int[] arr, long left, long right)

{

long middle; // индекс, по которому делим массив

if (left < right) // если есть более 1 элемента

{

middle = (left + right) / 2;

mergeSort(arr, left, middle); // сортировать левую половину

mergeSort(arr, middle+1, right); // сортировать правую половину

merge(arr, left, middle, right); // слить результаты в общий массив

}

7. Алгоритмы сортировки массивов со сложностью n²

Инэт – вики.

Сортировка пузырьком (англ. Bubble sort) — сложность алгоритма: O(n2); для каждой пары индексов производится обмен, если элементы расположены не по порядку.

Сортировка перемешиванием (Шейкерная, Cocktail sort, bidirectional bubble sort) — Сложность алгоритма: O(n2)

Гномья сортировка — имеет общее с сортировкой пузырьком и сортировкой вставками. Сложность алгоритма — O(n2).

Сортировка вставками (Insertion sort) — Сложность алгоритма: O(n2); определяем где текущий элемент должен находиться в упорядоченном списке и вставляем его туда

Димон Була

8. Алгоритмы сортировки массивов со сложностью n log n

Чаще всего встреч. в алгоритмах по принципу оббьем данных делится пополам.

1) Быстрая сортировка Хора – один из лучших алгоритмов для сортировки больших массивов, действует по принципу “Разделяй и властвуй”.Происходит разбиение массива на 2 части, относительно выбранного ключа, после чего обе части рекурсивно сортируются.

p-индекс начала, q-индекс середины,r-индекс конца массива. p<=q<r.

quickSort(p,r)

{

If(p<r) q = Partition(p, r); ϴ(n)

quickSort(p,q); T(n/2)

quickSort(q+1,r); T(n/2)

}

T(n)=2T(n/2)+n;

a=2, b=2;

f(n)=n; T(n) = ϴ(n log n);

2) Пирамидальная сортировка —превращаем список в кучу, берём наибольший элемент и добавляем его в конец списка/

Сортировка пирамидой использует сортирующее дерево(двоичное дерево, у которого

Каждый лист имеет глубину либо d, либо d − 1, d — максимальная глубина дерева.
Значение в любой вершине больше, чем значения её потомков.)

// см. ф-ии Heap и Build_H п. 13.

Heapsort(A){

Build_H(A)

for(int i = A.size;i>=1)

do Обменять A[0] и A[i]

heap_size[A] = heap_size[A] – 1;

Heap(0,A)

}

3) Сортировка слиянием (Merge sort)

Смотри вопрос 6

9. Алгоритмы сортировки массивов со сложностью n

1)Cортировка подсчетом. Основная идея сортировки подсчетом заключается в том, чтобы для каждого входного элемента х определить количество элементов, которые меньше X. С помощью этой информации элемент х можно разместить на той позиции выходного массива, где он должен находиться

CountingSort(int* A, int* B, int* C, int K)

{

for (int i = 0; i <= k; i++)

c[i] = 0;

for (int j = 0; j < n; j++)

C[A[j]]++;

for (int i = 2; i <= k; i++)

c[i] += c[i - 1];

for (j = n - 1; j > 0; j--)

{

B[C[A[j]]] = A[j];

C[A[j]]--;

}

2) Сортировка поразрядная.

RadixSort(A, d)

{

for(i=0;i<d;i++)

Устойчивая сортировка массива А по i-ой цифре

}

10. Линейные структуры данных, основные операции и характеристики

Линейные структуры данных – это структуры данных, в которых переход от одного элемента данных к другому не зависит от каких-либо логических условий, т.е. в линейных структурах используются лишь безусловные связи элементов. К линейным структурам относятся стеки, очереди, связанные списки.

Стеки и очереди — это динамические множества, элементы из которых удаляются с помощью предварительно определенной операции Delete. Первым из стека (stack) удаляется элемент, который был помещен туда последним: в стеке реализуется стратегия “последним вошел — первым вышел”. Аналогично, в очереди (queue) всегда удаляется элемент, который содержится в множестве дольше других: в очереди реализуется стратегия “первым вошел — первым вышел ”.

Операция вставки применительно к стекам часто называется Push (запись в стек), а операция удаления — Pop (снятие со стека).

Применительно к очередям операция вставки называется Enqueue (поместить в очередь), а операция удаления — DEQUEUE (вывести из очереди). Подобно стековой операции Pop, операция Dequeue не требует передачи элемента массива в виде аргумента.

11. Деревья, виды, способы представления, структуры данных

Поскольку любое дерево является графом, то задать его можна теми же способами что и граф: матрица и список смежности.

12. Двоичные деревья поиска, основные операции и характеристики

Деревья поиска представляют собой структуры данных, которые поддерживают многие операции с динамическими множествами, включая поиск элемента, минимального и максимального значения, предшествующего и последующего элемента, вставку и удаление.

В дополнение к полям ключа key и сопутствующих данных, каждый узел содержит поля left, right и р, которые указывают на левый и правый дочерние узлы и на родительский узел соответственно. Если дочерний или родительский узел отсутствуют, соответствующее поле содержит значение NIL. Единственный узел, указатель р которого равен nil, — это корневой узел дерева. Ключи в бинарном дереве поиска хранятся таким образом, чтобы в любой момент удовлетворять следующему свойству бинарного дерева поиска.

Если х — узел бинарного дерева поиска, а узел у находится в левом поддереве х, то key [у] <= key[х]. Если узел у находится в правом поддереве х, то key [х] <= key [у].

Свойство бинарного дерева поиска позволяет нам вывести все ключи, находящиеся в дереве, в отсортированном порядке с помощью простого рекурсивного алгоритма, называемого центрированным (симметричным) обходом дерева

Void Print(Tree Root)

{

If(root!=null){

Print(root.left);

Cons.WriteLine(root.key);

Print(root.right);

}

13. Двоичные кучи, основные операции и характеристики

Пирамида (binary heap) — это структура данных, представляющая собой объект-массив, который можно рассматривать как почти полное бинарное дерево/ Каждый узел этого дерева соответствует определенному элементу массива. На всех уровнях, кроме, может быть, последнего, дерево полностью заполнено (заполненный уровень — это такой, который содержит максимально возможное количество узлов). Последний уровень заполняется слева направо до тех пор, пока в массиве не закончатся элементы.

Различают 2 вида бинарных пирамид – неубывающие и невозрастающие.

Свойство невозрастающих пирамид (max-heap property) заключается в том, что для каждого отличного от корневого узла с индексом i выполняется следующее неравенство:

A [Parent (i)] >= А [i].

значение узла не превышает значение его родителя. В невозрастающей пирамиде самый большой элемент находится в корне дерева, а значения узлов поддерева, не превышают значения самого этого элемента.

Свойство неубывающих пирамид (min-heap property) A [Parent (i)] <= А [i]. Таким образом, наименьший элемент такой пирамиды находится в ее корне.

Основные операции:

void Heap(int I, int* A)

{

int l, r, largest, k;

l=2*i+1; r= 2*i+2;

if(l<size && A[l]>A[i])

largest = l; else largest = i;

if(r<size && A[r]>A[largest])

largest = r;

if(largest!=i) {k=A[i]; A[i]=A[largest]; A[largest]=k; Heap(largest,A);}

}

При вызове процедуры Heap предполагается, что бинарные деревья, корнями которых являются элементы l и r, являются невозрастающими пирамидами, но сам элемент А [i] может быть меньше своих дочерних элементов, нарушая тем самым свойство невозрастающей пирамиды. Функция Heap опускает значение элемента А [i] вниз по пирамиде до тех пор, пока поддерево с корнем, отвечающем индексу г, не становится невозрастающей пирамидой:

Если основное свойство не выполняется, устанавливаем элементы на свое место с помощью Heap.

void Build_H(int* A){ for(int i=size/2; i>=0;i--) Heap(i,A); }

Димон Смит

14. Хеш-таблицы, закрытое хеширование(инет)

В случае метода открытой адресации (или по-другому: метод закрытого хеширования) все элементы хранятся непосредственно в хеш-таблице, без использования связных списков. В отличии от хеширования с цепочками, при использовании метода открытой адресации может возникнуть ситуация, когда хеш-таблица окажется полностью заполненной, так что будет невозможно добавлять в неё новые элементы. Так что при возникновении такой ситуации решением может быть динамическое увеличение размера хеш-таблицы, с одновременной её перестройкой. Для разрешения же коллизий применяются несколько подходов. Самый простой из них – это метод линейного исследования. В этом случае при возникновении коллизии следующие за текущей ячейки проверяются одна за другой, пока не найдётся пустая ячейка, куда и помещается наш элемент. Так, при достижении последнего индекса таблицы, мы перескакиваем в начало, рассматривая её как «цикличный» массив. Одной из сложных вопросов реализации хеширования с открытой адресацией – это операция удаления элемента. Дело в том, что если мы просто удалим некий элемент их хеш-таблицы, то сделаем невозможным поиск ключа, в процессе вставки которого текущая ячейка оказалась заполненной. Так, мы можем помечать очищенные ячейки какой-то меткой, чтобы впоследствии это учитывать.

15. Хеш-таблицы, открытое хеширование(инет)

Открытое хеширование (или по-другому: метод цепочек) — простейший метод борьбы с коллизиями. При использовании этого метода мы объединяем все элементы, хешированные в одну и ту же ячейку, в связный список. Ячейка содержит указатель на заголовок списка всех элементов, хэш-значение ключа которых равно ; если таких элементов нет, ячейка содержит значение . Элементы вставляются в заголовок списка. Время, необходимое для вставки в наихудшем случае равно , учитывая то, что мы предполагаем отсутствие вставляемого элемента в таблице. Время поиска зависит от длины списка, и в худшем случае равно . Эта ситуация, когда все элементы хешируются в единственную ячейку. Если функция распределяем ключей по ячейкам таблицы равномерно, то в каждом списке будет содержаться порядка ключей. Это число называется коэффициентом заполнения хеш-таблицы. Математический анализ хеширования с цепочками показывает, что в среднем случае все операции в такой хеш-таблице в среднем выполняются за время .

16. Динамическое программирование, основные особенности

Динамическое программирование — способ решения сложных задач путём разбиения их на более простые подзадачи.

Ключевая идея в динамическом программировании достаточно проста. Как правило, чтобы решить поставленную задачу, требуется решить отдельные части задачи (подзадачи), после чего объединить решения подзадач в одно общее решение. Часто многие из этих подзадач одинаковы. Подход динамического программирования состоит в том, чтобы решить каждую подзадачу только один раз, сократив тем самым количество вычислений. Это особенно полезно в случаях, когда число повторяющихся подзадач экспоненциально велико.

17. Жадные алгоритмы, основные особенности

Жадный алгоритм — алгоритм, заключающийся в принятии локально оптимальных решений(лучших в данный момент) на каждом этапе, допуская, что конечное решение также окажется оптимальным.

Говорят, что к оптимизационной задаче применим принцип жадного выбора, если последовательность локально оптимальных выборов даёт глобально оптимальное решение. В типичном случае доказательство оптимальности следует такой схеме: Сначала доказывается, что жадный выбор на первом шаге не закрывает пути к оптимальному решению: для всякого решения есть другое, согласованное с жадным выбором и не хуже первого. Затем показывается, что подзадача, возникающая после жадного выбора на первом шаге, аналогична исходной, и рассуждение завершается по индукции.

18. Построение кода Хаффмена

Классический алгоритм Хаффмана на входе получает таблицу частот встречаемости символов в сообщении. Далее на основании этой таблицы строится дерево кодирования Хаффмана (Н-дерево).

1. Символы входного алфавита образуют список свободных узлов. Каждый лист имеет вес, который может быть равен либо вероятности, либо количеству вхождений символа в сжимаемое сообщение.

2. Выбираются два свободных узла дерева с наименьшими весами.

3. Создается их родитель с весом, равным их суммарному весу.

4. Родитель добавляется в список свободных узлов, а два его потомка удаляются из этого списка.

5. Одной дуге, выходящей из родителя, ставится в соответствие бит 1, другой — бит 0.

6. Шаги, начиная со второго, повторяются до тех пор, пока в списке свободных узлов не останется только один свободный узел. Он и будет считаться корнем дерева.

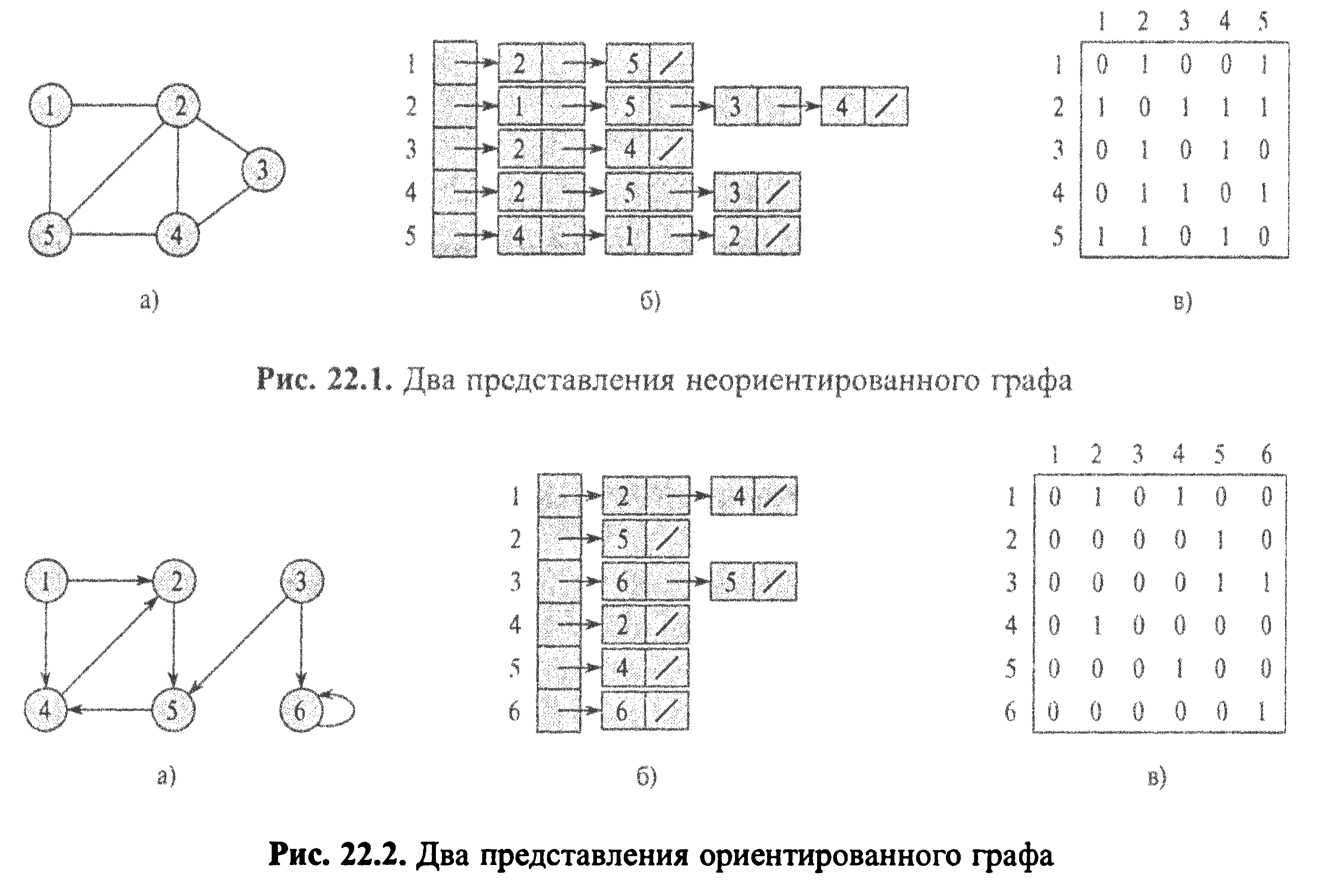
19. Представление ориентированных и не ориентированных графов

Есди используеться представление в виде списка, то для каждой вершины формируеться список вершин в которые можно из неё перейти.

Влад

20. Алгоритм обхода графов в ширину

(Метода Валенды)

Поиск в ширину

Название объясняется тем, что обход вершин графа осуществляется вширь, а не в глубь (сначала просматриваются все соседние вершины, затем соседи соседей и т.д.). Алгоритм использует очередь для хранения серых вершин. В самом начале все вершины помечаются белым цветом. Вершины помещеные в очередь красятся в серый цвет.

Алгоритм:

1) выбираем одну из вершин;

2) помечаем вершину серым цветом, помещаем в очередь;

3) пока очередь не пуста;

4) находим голову очереди;

5) все вершины, помеченные белым цветом, смежные с головой очереди помещаем в хвост очереди, красим в серый цвет;

6) красим голову очереди в черный цвет, удаляем из очереди

7) переходим к п.3;

(Алгоритм обхода графов в глубину

(Метода Валенды)

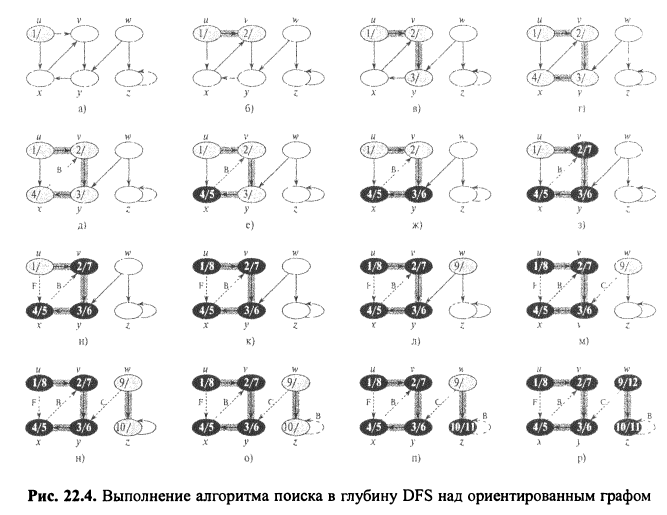
Поиск в глубину

Рассмотрим алгоритм обхода графа, основанный на методе поиска "в глубину". Цель задачи – пройти по всем вершинам графа и выдать список его вершин (в порядке обхода графа). В процессе обхода удобно помечать вершины тремя цветами, например, белым, серым и черным. Белым цветом отмечаются еще не пройденные вершины, серым – пройденные, но имеющие еще смежные не пройденные вершины, а черным – пройденные и не имеющие смежных не пройденных вершин. В самом начале все вершины помечаются белым цветом. Алгоритм следующий:

1) выбираем одну из вершин (обычно за основу берется первый элемент в списке смежных вершин или первая строка в матрице смежности);

2) помечаем вершину серым цветом;

3) проверяем, имеет ли вершина смежные ей вершины, помеченные белым цветом: если нет, то переходим к п.6;

4) запоминаем текущий номер вершины и переходим к одной из смежных (помеченных белым цветом);

5) переходим к п.2;

6) помечаем текущую вершину черным цветом, выводим на печать номер вершины и переходим к сохраненной ранее в п.4 вершине. Если таковой нет, значит, мы прошли по всем вершинам графа и вернулись к исходной, иначе – повторить шаги с п.2.

21. Остовое дерево, классификация ребер, топологическая сортировка

Остовым деревом называется антициклический подграф графа G. Минимальным остовым деревом – остовое дерево с минимальным весом. Вес дерева – сумма весов его дуг.

Ребра: положительные и отрицательные, направленные ненаправленные.Петлей называется ребро, инцидентное одной вершине.Ребро, имеющее направление, называется дугой. Ребра в дереве - обратные, прямые и перекрестные.

Классификация ребер при поиске в ширину

при поиске в ширину в неориентированном графе выполняются следующие свойства.

1) Не существует прямых и обратных ребер.

2) Для каждого ребра дерева (u, v) имеем d [v] = d [u] + 1.

3) Для каждого перекрестного ребра (u, v) имеем d [v] = d [u] или

d[v] = d [u] + 1.

при поиске в ширину в ориентированном графе вы-

выполняются следующие свойства.

1) Не существует прямых ребер.

2) Для каждого ребра дерева (u, v) имеем d [v] = d [u] + 1.

3) Для каждого перекрестного ребра (u, v) имеем d[v] ≤ d [u] + 1.

4) Для каждого обратного ребра (u, v) имеем 0 ≤ d [v] ≤ d [u].

Четыре типа ребер с использованием леса G_π, полу-полученного при поиске в глубину в графе G.

1. Ребра деревьев (tree edges) — это ребра графа G_π. Ребро (u, v) является ребром дерева, если при исследовании этого ребра открыта вершина v.

2. Обратные ребра (back edges) — это ребра (u,v), соединяющие вершину u с ее предком v в дереве поиска в глубину. Ребра-циклы, которые могут встречаться в ориентированных графах, рассматриваются как обратные

ребра.

3. Прямые ребра (forward edges) — это ребра (щу), не являющиеся ребрами дерева и соединяющие вершину u с ее потомком v в дереве поиска в глубину.

4. Перекрестные ребра (cross edges) — все остальные ребра графа. Они могут соединять вершины одного и того же дерева поиска в глубину, когда ни одна из вершин не является предком другой, или соединять вершины в разных деревьях.

Топологическая сортировка (topological sort) ориентированного ациклического графа G =

= (V, Е) представляет собой такое линейное упорядочение всех его вершин, что

если граф G содержит ребро (u,v) то u при таком упорядочении располагается

до v (если граф не является ацикличным, такая сортировка невозможна).

Топологическую сортировку графа можно рассматривать как такое упорядочение его

вершин вдоль горизонтальной линии, что все ребра направлены слева направо.

Вот простой алгоритм топологической сортировки ориентированного ацикли-

ациклического графа:

TopologicalJSort(G)

1 Вызов DFS(G) для вычисления времени завершения f[v] для каждой вершины v

2 По завершении работы над вершиной внести ее в начало связанного списка

3 return Связанный список вершин

Мы можем выполнить топологическую сортировку за время в (V + Е), по-

поскольку поиск в глубину выполняется именно за это время, а вставка каждой из

|V| вершин в начало связанного списка занимает время О(1).

Докажем корректность этого алгоритма с использованием следующей ключе-

ключевой леммы, характеризующей ориентированный ациклический граф.

22. Сильно связные компоненты, алгоритм поиска?

Сильно связный компонент ориентированного графа G = (V, Е) представляет собой максимальное множество вершин С V, такое что для каждой пары вершин u и v из С справедливо как uà v, так и v à u, т.е. вершины u и v достижимы друг из друга.

23. Построение минимального покрывающего дерева, алгоритм Крускала

(Построение минимального покрывающего дерева)

На каждом шаге алгоритма мы определяем ребро (u, v), которое можно добавить

к А без нарушения этого инварианта, в том смысле, что Аᴗ{(u,v)} также является подмножеством минимального остовного дерева. Мы назовем такое ребро безопасным (safe edge) для А, поскольку его можно добавить к А, не опасаясь нарушить инвариант.

Generic_MST(G, w)

1 А<-(Нолик зачеркнутый по диагонали)(хз но так в книге)(херь какая-то)

2 while А не является минимальным остовным деревом

3 do Найти безопасное для А ребро (u, v)

4 A<-Aᴗ{(u,v)}

5 return A

Мы используем инвариант цикла следующим образом.

Инициализация. После выполнения строки 1 множество А тривиально удовле-

удовлетворяет инварианту цикла.

Сохранение. Цикл в строках 2-4 сохраняет инвариант путем добавления только

безопасных ребер.

Завершение. Все ребра, добавленные в А, находятся в минимальном остовном

дереве, так что множество А, возвращаемое в строке 5, должно быть мини-

минимальным остовным деревом.

Самое важное, само собой разумеется, заключается в том, как именно найти

безопасное ребро в строке 3. Оно должно существовать, поскольку когда выпол-

выполняется строка 3, инвариант требует, чтобы существовало такое остовное дерево

Т, что A T. Внутри тела цикла while А должно быть истинным подмножеством Т, поэтому должно существовать ребро (u, v) Є Т, такое что (u, v) Є А и (u, v) —

безопасное для А ребро.

(Алгоритм Крускала)

Алгоритм Крускала непосредственно основан на обобщенном алгоритме

поиска минимального остовного дерева, приведенном в разделе 23.1. Он находит

безопасное ребро для добавления в растущий лес путем поиска ребра (u, v) с ми-

минимальным весом среди всех ребер, соединяющих два дерева в лесу. Обозначим

два дерева, соединяемые ребром (u, v), как С₁ и С₂- Поскольку (u, v) должно быть

легким ребром, соединяющим С₁ с некоторым другим деревом, из следствия 23.2

вытекает, что (u, v) — безопасное для С₁ ребро. Алгоритм Крускала является

жадным, поскольку на каждом шаге он добавляет к лесу ребро с минимально

возможным весом.

24. Построение минимального покрывающего дерева, алгоритм Прима

(Миним. ост дерево смотри в начале алгоритма Крускала)

(Алгоритм Прима)

Аналогично алгоритму Крускала, алгоритм Прима представляет собой част-

частный случай обобщенного алгоритма поиска минимального остовного дерев.

Алгоритм Прима обладает тем свойством, что ребра в множестве А всегда образуют

единое дерево. Дерево начинается с произвольной корневой вершины u и растет до тех пор, пока не охватит все вершины в V. На каждом шаге к дереву А добавляется легкое ребро, соединяющее дерево и отдельную вершину из оставшейся части графа. Данное правило добавляет только безопасные для А ребра; следовательно, по завершении алгоритма ребра в А образуют минимальное остовное дерево.

Данная стратегия является жадной, поскольку на каждом шаге к дереву добавляется ребро, которое вносит минимально возможный вклад в общий вес.

Воспользуйтесь поиском по сайту: