 |
Классификация задач оптимизации. http://works.tarefer.ru/50/100248/index.html
|
|
|
|
Задача о рациональном питании (задача о пищевом рационе).
ПОСТАНОВКА ЗАДАЧИ. Ферма производит откорм скота с коммерческой целью. Для
простоты допустим, что имеется всего четыре вида продуктов: П1, П
2, П3, П4; стоимость единицы каждого продукта равна
соответственно С1, С2, С3, С4. Из
этих продуктов требуется составить пищевой рацион, который должен содержать:
белков – не менее b i единиц; углеводов – не менее b
2 единиц; жиров – не менее b 3 единиц. Для продуктов П
1, П2, П3, П4 содержание белков,
углеводов и жиров (в единицах на единицу продукта) известно и задано в таблице,
где a ij (i=1,2,3,4; j=1,2,3) – какие – то определённые
числа; первый индекс указывает номер продукта, второй – номер элемента (белки,
углеводы, жиры).
| продукт | элементы | ||
| белки | углеводы | жиры | |
| П1 П2 П3 П4 | A11 A21 A31 A41 | A12 A22 A32 A42 | A13 A23 A33 A43 |
Требуется составить такой пищевой рацион (т.е. назначить количества продуктов П
1, П2, П3, П4, входящих в него), чтобы
условия по белкам, углеводам и жирам были выполнены и при этом стоимость
рациона была минимальна.
МАТЕМАТИЧЕСКУЮ МОДЕЛЬ. Обозначим x 1, x 2,
x 3, x 4 количества продуктов П1, П
2, П3, П4, входящих в рацион. Показатель
эффективности, который требуется минимизировать, - стоимость рациона (обозначим
её L): она линейно зависит от элементов решения x 1, x
2, x 3, x 4.
Целевая функция: 
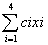
Система ограничений:
a 11 x 1+ a 21 x 2+ a 31 x 3+ a 41 x 4≥ b 1
a 12 x 1+ a 22 x 2+ a 32 x 3+ a 42 x 4≥ b 2
a 13 x 1+ a 23 x 2+ a 32 x 3+ a 43 x 4≥ b 3
Эти линейные неравенства представляют собой ограничения, накладываемые на
элементы решения x 1, x 2, x 3
, x 4.
Таким образом, поставленная задача сводится к следующей: найти такие
неотрицательные значения переменных x1, x2, x3
|
|
|
, x4, чтобы они удовлетворяли ограничениям – неравенствам и
одновременно обращали в минимум линейную функцию этих переменных:

Задача о планировании производства.
ПОСТАНОВКА ЗАДАЧИ. Предприятие производит изделия трёх видов: U1, U
2, U3. По каждому виду изделия предприятию спущен план, по
которому оно обязано выпустить не мене b 1 единиц изделия U
1, не мене b 2 единиц изделия U2 и не мене
b 3 единиц изделия U3. План может быть перевыполнен, но
в определённых границах; условия спроса ограничивают количества произведённых
единиц каждого типа: не более соответственно b 1, b
2, b 3 единиц. На изготовление изделий идёт какое-то
сырьё; всего имеется четыре вида сырья: s 1, s 2
, s 3, s 4, причём запасы ограничены числами
g 1, g 2, g 3, g 4
единиц каждого вида сырья. Теперь надо узнать какое количество сырья каждого
вида идёт на изготовление каждого вида изделий. Обозначим a ij
количество единиц сырья вида s i (I= 1, 2, 3, 4), потребное на
изготовление одной единицы изделия Uj (j= 1, 2, 3). Первый индекс у
числа a ij – вид изделия, второй – вид сырья. Значения a
ij сведены в таблицу (матрицу).
| Сырьё | Изделия | ||
| U1 | U2 | U3 | |
| S1 S2 S3 S4 | a11 a12 a13 a14 | a21 a22 a23 a24 | a31 a32 a33 a34 |
При реализации одно изделие U1 приносит предприятию прибыль c
1, U2 – прибыль c 2, U3 – прибыль
c 3. Требуется так спланировать производство (сколько каких
изделий производить), чтобы план был выполнен или перевыполнен (но при
отсутствии «затоваривания»), а суммарная прибыль обращалась в максимум.
МАТЕМАТИЧЕСКАЯ МОДЕЛЬ. Элементами решения будут x 1, x
2, x 3 – количества единиц изделий U1, U
2, U3, которые мы произведём. Обязательность выполнения
планового задания запишется в виде трёх ограничений – неравенств: x
1³ b 1, x 2³ b 2
, x 3³ b 3.
Отсутствие изделий продукции (затоваривания) даёт нам ещё три ограничения –
неравенства: x 1£ b 1, x
2£ b 2, x 3£ b 3
.
Целевая функция: L= c 1 x 1+ c 2 x 2+ c 3 x 3→ max.
|
|
|
Система ограничений:
a 11 x 1+ a 21 x 2+ a 31 x 3£ ¡ 1.
a 12 x 1+ a 22 x 2+ a 32 x 3£ ¡ 2.
a 13 x 1+ a 23 x 2+ a 33 x 3£ ¡ 3.
a 14 x 1+ a 24 x 2+ a 34 x 3£ ¡ 4.
Задача о загрузки оборудования.
ПОСТАНОВКА ЗАДАЧИ. Ткацкая фабрика располагает двумя видами станков, из них N1
станков типа 1 и N2 станков типа 2. Станки могут производить три вида тканей:
T1, T2, T3, но с разной производительностью. Данные a ij
производительности станков в таблице (первый индекс – тип станка, второй – вид
ткани).
Каждый метр ткани вида T1 приносит фабрике доход c 1, вида Т2
– доход с 2, Т3 – доход с 3.
| Тип станка | Вид ткани | ||
| Т1 | Т2 | Т3 | |
| а11 а21 | а12 а22 | а13 а23 |
Фабрике предписан план согласно которому она должна производить в месяц не менее
b 1 метров ткани Т1, b 2 метров ткани Т2, b
3 метров ткани Т3; количество метров каждого вида ткани не должно
превышать соответственно b 1, b 2, b
3 метров. Кроме того, все без исключения станки должны быть загружены.
Требуется так распределить загрузку станков производством тканей Т1, Т2, Т3,
чтобы суммарный месячный доход был максимален.
МАТЕМАТИЧЕСКАЯ МОДЕЛЬ. Введём букву x с двумя индексами (первый – тип станка,
второй – вид ткани). Всего будет шесть элементов решения: x 11
x 12 x 13 x 21 x 22
x 23.
Здесь x 11 – количество станков типа 1, занятых изготовлением
ткани Т1, x 12 – количество станков типа 1, занятых
изготовлением ткани Т2 и т.д.
Запишем суммарный доход от производства всех видов тканей. Суммарное количество
метров ткани Т1, произведённое всеми станками, будет равно a11x
11+a21x21 и принесёт доход c1(a11
x11+a21x21).
Целевая функция: L= c 1 (a 11 x 11
+ a 21 x 21)+ c 2 (a
12 x 12+ a 22 x 22)+ c
3 (a 13 x 13+ a 23 x
23) 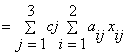 →
→
max.
Система ограничений:
Обеспечим выполнения плана ограничениями по минимальным параметрам:
a 11 x 11+ a 21 x 21³ b 1,
a 12 x 12+ a 22 x 22³ b 2,
a 13 x 13+ a 23 x 23³ b 3,
После этого ограничим выполнение плана по максимальным параметрам:
a 11 x 11+ a 21 x 21£ b 1,
a 12 x 12+ a 22 x 22£ b 2,
a 13 x 13+ a 23 x 23£ b 3,
Теперь запишем ограничения, связанные с наличием оборудования и его полной
загрузкой. Суммарное количество станков типа 1, занятых изготовлением всех
тканей, должно быть равно N1; типа 2 – N2.
x 11+ x 12+ x 13=N1,
x 21+ x 22+ x 23=N2,
Задача о снабжении сырьём.
ПОСТАНОВКА ЗАДАЧИ. Имеется три промышленных предприятия: П1, П2
|
|
|
, П3, требующих снабжения определённым видом сырья. Потребности в
сырье каждого предприятия равны соответственно a 1, a
2, a 3 единиц. Имеются пять сырьевых баз, расположенных
от предприятий на каких – то расстояниях и связанных с ними путями сообщения с
разными тарифами. Единица сырья, получаемая предприятием Пi c базы Б
j , обходится предприятию в с ij рублей
(первый индекс – номер предприятия, второй – номер базы).
| Предприятия | Базы | ||||
| Б1 | Б2 | Б3 | Б4 | Б5 | |
| П1 П2 П3 | С11 С21 С31 | С12 С22 С32 | С13 С23 С33 | С14 С24 С34 | С15 С25 С35 |
Возможности снабжения сырьём с каждой базы ограничены её производственной
мощностью: базы Б1, Б2, Б3, Б4, Б
5 могут дать не более b 1, b 2, b
3, b 4, b 5 единиц сырья. Требуется
составить такой план снабжения предприятий сырьём (с какой базы, куда и какое
количество сырья везти), чтобы потребности предприятий были обеспечены при
минимальных расходах на сырьё.
МАТЕМАТИЧЕСКАЯ МОДЕЛЬ. Обозначим x ij количества сырья с j –
ой базы. Всего план будет состоять из 15 элементов решения: x 11
x 12 x 13 x 14 x 15
x 21 x 22 x 23 x 24
x 25 x31 x 32 x 33
x 34 x 35.
Целевая функция:
Система ограничений:
x 11+ x 12+ x 13+ x 14+ x 15= a 1,
x 21+ x 22+ x 23+ x 24+ x 25= a 2,
x 31+ x 32+ x 33+ x 34+ x 35= a 3,
x 11+ x 21+ x 31£ b 1,
x 12+ x 22+ x 32£ b 2,
x 13+ x 23+ x 33£ b 3, (4.3.)
x 14+ x 24+ x 34£ b 4,
x 15+ x 25+ x 35£ b 5,
|
|
|


