 |
Деление окружности на равные части
|
|
|
|
Деление окружности на равные части
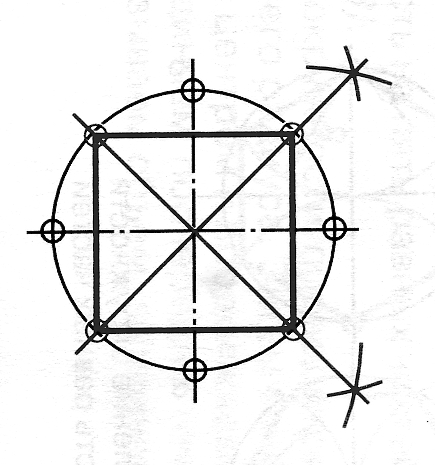
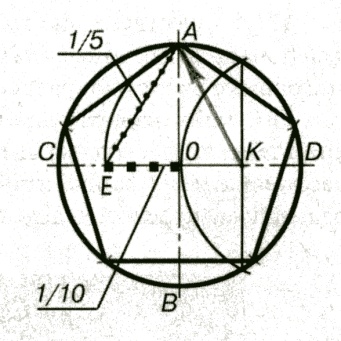
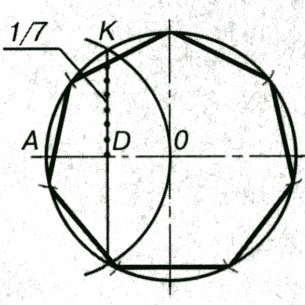
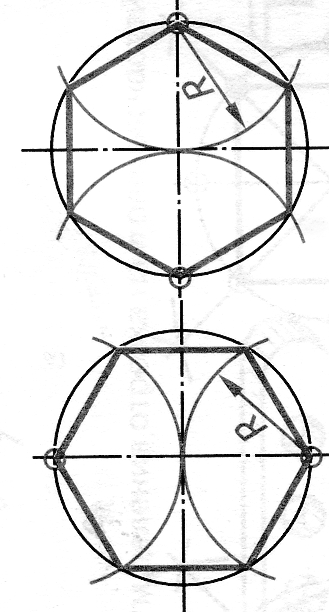
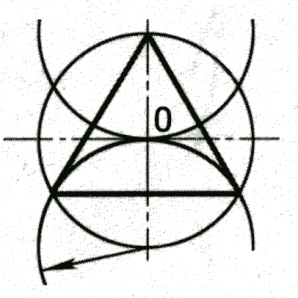Некоторые детали имеют элементы, равномерно распределенные по окружности. При выполнении чертежей деталей, имеющих подобные элементы, необходимо уметь делить окружность на равные части.
| |  | 
| ||||
 | 
| 
| ||||
| | 
|
Сопряжения
При вычерчивании деталей машин и приборов, встречаются детали, контуры очертаний которых имеют плавные переходы одной линии в другую
Сопряжением называется плавный переход от одной линии к другой.
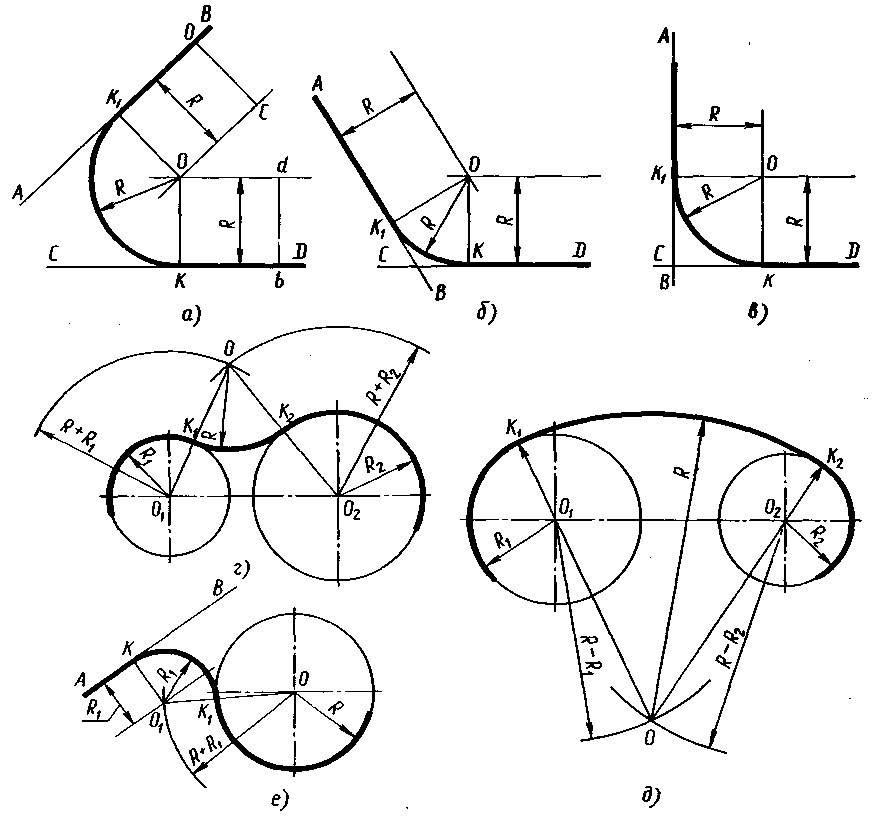Для построения сопряжений надо знать величину радиуса сопряжений, найти центр, из которого проводят дугу, т. е. центр сопряжений. Затем нужно найти точки, в которых одна линия переходит в другую, т. е. точки сопряжений. Одновременно следует помнить, что без точного построения центра и точек сопряжения невозможно правильно выполнить и обвести чертеж. Точка сопряжения дуги окружности и прямой линии лежит на перпендикуляре, опущенном из центра дуги на сопрягаемую прямую, или на линии, соединяющей центры сопрягаемых дуг.
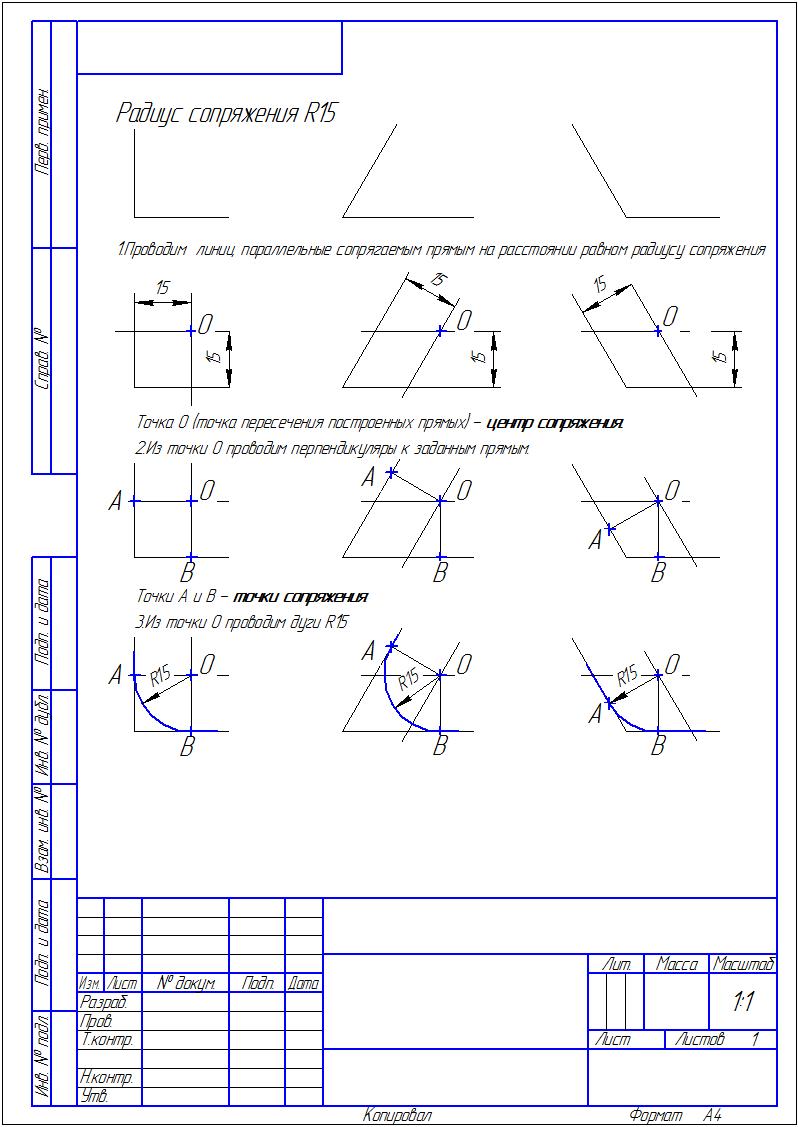
Для построения сопряжения нужно найти три точки: центр сопряжения, точки сопряжения. Радиус сопряжения обычно задан. Центр и точки сопряжения определяются графически.
Последовательность построения сопряжения прямых (углов)
сопряжение дуги окружности радиусом R1 прямой линии a дугой окружности радиуса R с внешним касанием.
сопряжения, при вычерчивании которого необходимо построение внутреннего и внешнего сопряжения.
При внутреннем сопряжении центры сопрягаемых дуг О1 и О2 находятся внутри сопрягающей дуги радиуса R (рисунок 37, а).
|
|
|
При внешнем сопряжении центры сопрягаемых дуг О1 и О2 находятся вне сопрягающей дуги радиуса R (рисунок 37, б).
а) б)
Л екальные кривые
В технике встречаются детали, поверхности которых образованы перемещением кривых линий: эллипса, эвольвенты окружности, спирали Архимеда и др. Кривые линии нельзя точно вычертить циркулем, поэтому отдельные точки этих кривых соединяют плавными линиями при помощи лекал. Отсюда название - лекальные кривые.
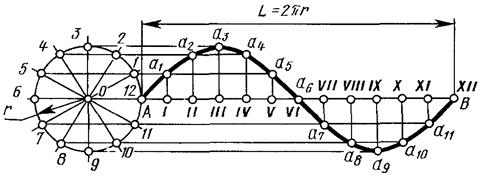Синусоидой называют плоскую кривую, изображающую изменение синуса в зависимости от изменения его угла. Для построения синусоиды нужно разделить окружность на равные части и на такое же количество равных частей разделить отрезок прямой
АВ = 2лR. Из одноименных точек деления провести взаимно перпендикулярные линии, в пересечении которых получают точки, принадлежащие синусоиде.
Содержание листа:
Задание по теме: «Геометрические построения» включает в себя следующие графические задачи:
задача №1. Построение изображения контура детали, применив правила сопряжения и деления окружности на равные части
задача №2 Построение синусоиды.
задача №3. Построение овала.
Графическая работа выполняется на листе формата А3 (297 х 420 мм).
Лист содержит рамку, ограничивающую поле чертежа, и основную надпись по ГОСТ 2. 104-68. В зависимости от размеров, указанных в задании, выбирается масштаб чертежа. При этом допускается применять 2 масштаба - один указывается в основной надписи, второй - над изображением детали.
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
В соответствие с примером оформления задания и исходными данными выполнить в тонких линиях свой вариант задания.
Порядок выполнения листа:
- определить задание согласно своему варианту;
- выбрать масштаб;
- формат А3 расположить горизонтально;
- выполнить внутреннюю рамку и основную надпись;
- внимательно изучитьгеометрические фигуры, подлежащие вычерчиванию и выполнить разметку листа, определив место для изображения каждой задачи;
- разметить на листе габаритные рамки двух деталей и положение осевых и центровых линий локальной кривой;
- выполнить построения каждого изображения в тонких линиях по заданным параметрам;
- проверить построения;
- выполнить обводку чертежа, рамки и граф основной надписи;
10. нанести размеры, надписи на чертеже и заполнить основную надпись;
|
|
|
|
|
|
