 |
Расчёт и построение меридианного сечения колеса.
|
|
|
|
Меридианным сечением рабочего колеса называется сечение колеса плоскостью, проходящей через ось колеса. При этом лопасти рабочего колеса не рассекаются, а входная и выходная кромки лопасти наносятся на секущую плоскость круговым проектированием, т.е. каждая точка кромок лопасти проворачивается вокруг оси колеса до встречи с секущей плоскостью.
Профилирование меридианного сечения ведётся так, чтобы ширина межлопастного канала рабочего колеса изменялась плавно от входа к выходу. Для этого, обычно, задаются графиком изменения меридианной составляющей абсолютной скорости 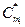 в функции от радиуса
в функции от радиуса 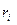 или длины средней линии межлопастного канала. Форма средней линии межлопастного канала рабочего колеса выбирается по прототипам в зависимости от величины коэффициента быстроходности
или длины средней линии межлопастного канала. Форма средней линии межлопастного канала рабочего колеса выбирается по прототипам в зависимости от величины коэффициента быстроходности 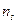 .
.
Исходным уравнением для определения ширины межлопастного канала является уравнение неразрывности:
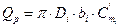 , где
, где
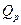 - расчетная подача,
- расчетная подача,  ;
;
 - некоторый произвольный диаметр, [м];
- некоторый произвольный диаметр, [м];
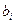 - ширина межлопастного канала на диаметре, [м];
- ширина межлопастного канала на диаметре, [м];
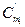 - меридианная составляющая абсолютной скорости,
- меридианная составляющая абсолютной скорости, 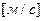 ;
;
 ;
;
 =0.0078 [м];
=0.0078 [м];
1.4 Расчёт и построение цилиндрической лопасти рабочего колеса в плане.
Планом рабочего колеса называется сечение, полученное средней поверхностью тока и спроектированное на плоскость, нормальную к оси насоса. Сечение лопасти в плане строится по средней линии и толщине лопасти на соответствующих радиусах. Средняя линия сечения лопасти делит пополам толщину лопасти, отсчитываемую по нормали к средней линии лопасти.
Профилирование лопасти следует вести так, чтобы обеспечить возможно более благоприятные условия для безотрывного обтекания контура лопасти потоком рабочей среды. В этом случае гидравлические потери будут минимальными.
|
|
|
В тихоходных колёсах с цилиндрическими лопастями, у которых средняя линия канала в меридианном сечении имеет направление, близкое к радиальному, сечение лопасти в плане можно принять за истинное сечение лопасти поверхностью тока.
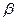 -угол установки лопасти;
-угол установки лопасти;
dr - приращение радиуса;
Тогда дифференциальное уравнение средней линии будет иметь вид:
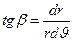 , откуда
, откуда 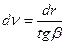 , при
, при  ,
,  и тогда
и тогда 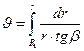
Угол установки лопасти колеса на соответствующем радиусе может быть определён по зависимости:
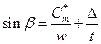 , где
, где
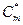 - меридианная составляющая абсолютной скорости;
- меридианная составляющая абсолютной скорости;
 - относительная скорость;
- относительная скорость;
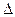 - толщина лопасти;
- толщина лопасти;
t - шаг на соответствующем радиусе.
Так как значениями угла 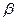 , толщиной лопасти
, толщиной лопасти  , скоростями
, скоростями 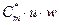 в функции радиуса задаются, как правило, не аналитически, а в виде графиков или таблиц, интегрирование уравнения
в функции радиуса задаются, как правило, не аналитически, а в виде графиков или таблиц, интегрирование уравнения
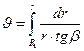 выполняется обычно приближённо по правилу трапеции.
выполняется обычно приближённо по правилу трапеции.
Обозначим подынтегральную функцию 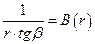 . Тогда
. Тогда 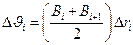 , где
, где
 - приращение центрального угла;
- приращение центрального угла;
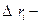 приращение радиуса;
приращение радиуса;
 - значения подынтегральной функции в начале и в конце рассматриваемого участка.
- значения подынтегральной функции в начале и в конце рассматриваемого участка.
Тогда  а величина радиуса вычисляется по уравнению
а величина радиуса вычисляется по уравнению
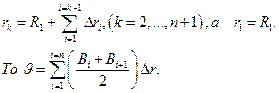
Указанные расчёты удобно проводить в табличной форме (табл.1).
Таблица 1. Расчет лопасти в плане
| № | Ri | С' mi | bi | Wi | C'mi/Wi | ti | Δi | Δi/ti | sin βi | βi | tg βi | Bi | Δri | (Bi+B(i-1))/2 | Δν | ν | νi,град |
| 0,067 | 0,0326 | 2,766 | 9,670 | 0,2860 | 0,05296 | 0,00200 | 0,03777 | 0,3238 | 18,892 | 0,3422 | 43,317 | ||||||
| 0,073 | 0,0310 | 2,807 | 9,683 | 0,2899 | 0,05702 | 0,00290 | 0,05086 | 0,3408 | 19,924 | 0,3625 | 37,983 | 0,00517 | 40,650 | 0,2103 | 0,210 | 12,048 | |
| 0,078 | 0,0293 | 2,849 | 9,696 | 0,2938 | 0,06108 | 0,00350 | 0,05730 | 0,3511 | 20,555 | 0,3750 | 34,275 | 0,00517 | 36,129 | 0,1869 | 0,397 | 22,755 | |
| 0,083 | 0,0277 | 2,890 | 9,709 | 0,2977 | 0,06514 | 0,00365 | 0,05604 | 0,3537 | 20,715 | 0,3782 | 31,868 | 0,00517 | 33,072 | 0,1711 | 0,568 | 32,557 | |
| 0,088 | 0,0260 | 2,932 | 9,722 | 0,3016 | 0,06920 | 0,00385 | 0,05564 | 0,3572 | 20,928 | 0,3824 | 29,664 | 0,00517 | 30,766 | 0,1591 | 0,727 | 41,675 | |
| 0,093 | 0,0243 | 2,973 | 9,735 | 0,3054 | 0,07326 | 0,00400 | 0,05460 | 0,3600 | 21,101 | 0,3859 | 27,768 | 0,00517 | 28,716 | 0,1485 | 0,876 | 50,186 | |
| 0,098 | 0,0227 | 3,015 | 9,748 | 0,3093 | 0,07732 | 0,00390 | 0,05044 | 0,3597 | 21,082 | 0,3855 | 26,336 | 0,00517 | 27,052 | 0,1399 | 1,016 | 58,204 | |
| 0,104 | 0,0210 | 3,056 | 9,761 | 0,3131 | 0,08138 | 0,00365 | 0,04485 | 0,3580 | 20,974 | 0,3834 | 25,163 | 0,00517 | 25,749 | 0,1332 | 1,149 | 65,835 | |
| 0,109 | 0,0194 | 3,098 | 9,774 | 0,3169 | 0,08544 | 0,00325 | 0,03804 | 0,3550 | 20,791 | 0,3797 | 24,198 | 0,00517 | 24,680 | 0,1277 | 1,277 | 73,150 | |
| 0,114 | 0,0177 | 3,139 | 9,787 | 0,3207 | 0,08950 | 0,00240 | 0,02682 | 0,3476 | 20,338 | 0,3707 | 23,662 | 0,00517 | 23,930 | 0,1238 | 1,400 | 80,242 | |
| 0,119 | 0,0161 | 3,181 | 9,800 | 0,3246 | 0,09356 | 0,3246 | 18,938 | 0,3431 | 24,452 | 0,00517 | 24,057 | 0,1244 | 1,525 | 87,372 |
|
|
|

Проверочный расчёт на кавитацию.
 3.042 м/с;
3.042 м/с;
 20.98 м/с;
20.98 м/с;
 20.759 м/с;
20.759 м/с;
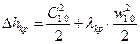 ;
;
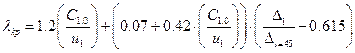 =
=
= 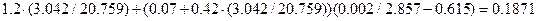
где  ;
;
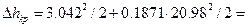 45.795 Дж/кг
45.795 Дж/кг
 =
=  973.248;
973.248;

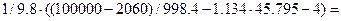 4.3
4.3
Вывод: Проведя расчет на кавитацию видно, что 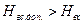 (4.3 > -4). Следовательно, при данных условиях кавитации в насосе не будет.
(4.3 > -4). Следовательно, при данных условиях кавитации в насосе не будет.
|
|
|


