 |
Определение теории графов. Задачи оптимизации на графах.
|
|
|
|
Дискретные СВ. Числовые х-ки и их св-ва.
Если пр-во элементарных событий конечно или счетно, то СВ можно задать перечислив все ее возможные знач-я. Такую СВ наз. дискретной.
З-н распр-я – известны всевозможные знач-я СВ и соотв. им вер-ти.
Осн. св-во дискр. з-на распр-я 
,
Числовые х-ки – это параметры, характеризующие ожидаемое истинное значение СВ (мера случайной тенденции или мера положения) и разброс значений СВ 
относит. центра (мера масштаба или сдвига).
Параметрами, х-ющими меру положения, явл-ся мат. ожидание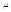 
, мода 
, медиана 
.
Мат.ожиданием явл-ся абстрактный аналог истинного знач-я x.
x- дискретная: 
- возможные принимаемые знач-я; 
- их вероятности.
- непрерывная 
, 
- плотность распр-я вер-ти.
Св-ва: 1) 
2) 
: 
3) 
4) 
- независимые СВ, то 
Геом. и физ. Смысл m:абсцисса центра тяжести криволинейной трапеции, ограниченной графиком пл-ти. Модой наз-ся наиболее вероятностное значение СВ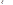 
(для дискр. СВ). Медиана – знач-е СВ, для кот вып-ся. 
Дисперсия х-ет меру разброса СВ относ. среднего:
x- дискретная: 
, 
непрерывная 
Св-ва: 1)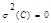 
: 
2) 
: 
3) 
- независимые СВ, 
4) - независимые, 
- показатель степени связности 
и 
, наз. ковариацией 
. Если - независимые, то 
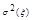- среднее квадратич. отклонение. m и 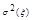- два основных параметра, кот полностью х-ют нормальный з-н распределения.
Нач-ным моментом k -го порядка наз-ся вел-на вида 
. МО – нач. момент 1-го порядка.
Центральным моментом k -го порядка наз-ся вел-на вида 
.
Дисперсия – центральный момент 2-го порядка. Центр. момент 3-го порядка – асимметрия (симметрия относ. Ох). Центр. момент 4-го порядка – эксцесс (симметрия относ Оу).
Методы комбинаторного анализа и их применение для реш-я задач.
Комбинаторный анализ зан-ся решением задач пересчета (ск-ко сущ. объектов, обладающих заданным св-вом) и задач перечисления (ск-ко и какие эл-ты обладают заданным св-вом).
|
|
|
1) Правило суммы. Если объект А м. б. выбран m СП-бами, а объект В др. n сп-бами, то выбор либо А, либо В можно осущ. 
сп-бами
, тогда когда 
, 
2) Правило произведения. Если объект А м. б. выбран m СП-бами, и после каждого из таких выборов объект В м.б. выбран n сп-бами, то выбор А и В можно осущ. 
сп-бами
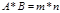
Перестановка – конечное упорядоченное мн-во, содержащее n различных эл-тов, кот. можно получить из заданного неупорядоченного мн-ва, сост. из n эл-тов. 
выборка – набор эл-тов вида 
из мн-ва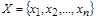 
, наз. выборкой объема r из n эл-тов.
Размещение – упорядоченная 
выборка (
) 
(сколькими СП-бами из n предметов можно выбрать r и разместить на r различных мест)
Сочетание – неупорядоченная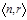 
выборка () 
(сколькими СП-бами из n предметов можно выбрать r)
Методы комбинаторного анализа.
Элементарные рекуррентные соотн-я.
- рекуррентное ур-е
Для реш-я общего вида рекуррентных соотн-й общих правил не сущ., но наиболее часто встречающийся случай имеет общий алгоритм реш-я.
(*)
Правило реш-я рекуррентного ур-я.
Шаг1. Сост. х-кое ур-е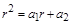 
(с теми же коэф, что и рекурент. ур-е)
Шаг2. Если корни х-кого ур-я не кратны, то общее реш-е ур-я имеет вид:
, где 
и 
- нек. числа.
2) Метод производящих ф-й – неэлементарный.
- перечисляющая производящая ф-я сочетаний из n различных объектов или n -нумератор.
Обычной производящей ф-ей для посл-ти 
наз сумма вида 
Реш-е лин. рекуррентных ур-й с пом. производящих ф-й.
1) Умножить каждое лин. n -тое соотн-е на 
2) Полученные ур-я сложить.
Метод включения и исключения.
Явл. обобщением правила суммы в случае, если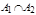 
С пом. так. метода решаются возможности разделения мн-в на подмн-ва в зависимости от обладания их эл-тами нек. св-ми
Определение теории графов. Задачи оптимизации на графах.
|
|
|
Графом G называют пару множеств (V,E), где V={1,2,..,n} – множество пронумерованных вершин, т. е. V={V1,V2,…,Vn }, а E={e} – набор упорядоченных или неупорядоченных пар вершин e={vi,vj}. Неупорядоченная пара вершин, называется ребром, а упорядоченная - дугой.
Граф содержащий только рёбра(дуги), называется неориентированным ( ориентированным). Граф, содержащий кратные ребра, называется мультиграфом.
Вершины V1, V2 называются смежными, ели они образуют ребро или дугу e={V1,V2}. Говорят, что V1, V2 инциденты ребру (дуге) e.
Каждому n-вершинному графу соответствует матрица смежности n x n C=||Cij||, Cij= количество ребер, соединяющих вершины iи j. (С – диагональные элементы = 0; симметрична относительно диагонали;)
Граф G¢=(V¢,E¢) называется частью графа G=(V,E), если V¢ÍV, E¢ÍE, причем G¢ и G не изоморфны
(def Графы G1 и G2называются изоморфнышми, если на множестве их вершин можно установить взаимно однозначное соответствие сохраняющие отношение смежности вершин на этих мн-вах ).
Часть G¢ графа G называется суграфом, если V¢= V, E¢ÌE. G¢ называется подграфом, если V¢ÌV, а E состоит только из некоторых ребер e={vi,vj} таких, что оба их конца vi,vjÎV¢.
|V|, |E| - величины показывающие количество вершин и ребер графа соответственно.
По количеству ребер можно выделить следующие виды:
1. En |V| = n, |E| = 0 – пустой граф (груда);
2. Противоположный Еn, Kn полный граф (клика), у которого все вершины попарно смежны. Число ребер в n-мерной клике n(n-1)/2;
3. Граф имеющий вид многоугольника называется циклом.
Маршрутом длины k называется такая последовательность L=(e1,…,ek) ребер графа G, в который конец предыдущего ребра является началом следующего, а k – равно количеству ребер последовательности.
Маршрут в котором все ребра различны называется цепью.
Цепь в которой все вершины различны называется простой цепью.
Маршрут называется замкнутым, если в нем начальная и конечная вершины совпадают.
Замкнутый маршрут в котором ребра не повторяются называется циклом и если не повторяются и вершины то – простым циклом.
Если простой цикл содержи все вершины данного графа то он называется гамильтоновым.
Граф наз. связным, если для любой пары вершин сущ-ет маршрут соединяющий эти вершины в данном графе.
|
|
|
Для графа можно определить матрицу расстояний D = ||dij||, где dij – длина кратчайшей простой цепи между вершинами i и j.
Диаметром графа G называется величина diam(G) = max(dij)
Степенью S(i) вершины iÎV называется число ребер, инцидентных ей.
Степенью графа называется величина 
.
Граф называется однородным, если степени его вершин одинаковы.
Граф G называется эйлеровым ó когда G связный и все вершины имеют четную степень.
Связный граф не содержащий циклов называется деревом.
Остовным деревом графа называется связный суграф этого графа не содержащий циклов.
Теорема: для любого натурального n>=2 количество всех остовных деревьев в полном n – вершинном графе равно nn-2.
Задачи оптимизации на графах:
1. Задача о минимальном остовном дереве;
Постановка задачи: имеется n объектов которые необходимо соединить коммуникационной сеткой и между объектами известны стоимости прокладки. Задана матрица смежности С =||cij||n*n, где cij – стоймость прокладки между пунктами i и j.
Математическая постановка задачи:
Дан n вершинный граф, каждому ребру которого ставится в соответствие cij. Множесто допустимых решений явл. связанные суграфы.
Алгоритм Краскала
Исходные данные: связный взвешенный граф с n >0 вершинами.
1. построить пустой граф с n вершинами;
2. k =0;
3. если k = n -1, то конец;
4. k = k +1;
5. найти k -ое по возрастанию весов ребро графа;
6. если добавление ребра в граф не приводит к появлению цикла, то добавить его;
7. перейти к шагу 3.
КОНЕЦ
2. Задача раскраски графа;
Постановка задачи: правильно раскрасить граф, т.е. такое приписывание вершинам графа номеров цветов, что любые две вершины имеют разную окраску.
3. Задача о кратчайшем пути между парой вершин;
Постановка задачи: если граф невзвешенный, то получаем задачу поиска пути лабиринта; если граф взвешенный -> задача нахождения кратчайшего пути, при этом задана стоимость прохождения.
|
|
|
