Краткий анализ основ геометрий 15 глава

Поставим еще одну точку. Структуризация возросла. Между точками по различным критериям может быть найдена активная область или нейтральная зона, разделяющая как их, так и плоскость листа. Или они могут быть соединены одной линией, которая делит лист уже на две иные, чем нейтральная линия, части, создавая иные пространства по обе ее стороны.

Соединим точки линией и в одном из образовавшихся пространств, в стороне от линии поставим точку, создав тем самым все необходимые предпосылки для формулирования или пятой аксиомы Евклида или основной аксиомы динамики пространства. Все имеющиеся на плоскости элементы равнозначны или, по современной артикуляции, равноправны, и только движение определяет их принадлежность к динамике. Если теперь со стороны прямой, восстановив до точки М образующий луч, двигать его неизменным по длине вдоль прямой, то точка, в которую он вошел, будет оставлять след евклидовой прямой, параллельной базовой. И это будет продолжаться бесконечно, если... если мы не последуем за Дезаргом. Дезарг, исходя из кажущегося пересечения в перспективе параллельных в одной точке, предложил считать пересечения проекциями «бесконечно удаленных» точек, равноправными со всеми остальными элементами. Так в проективную геометрию вошли «несобственные (бесконечно удаленные) точки» и «несобственные плоскости» - плоскости, на которых лежат эти точки.

Введение «несобственных» точек и плоскостей нарушило равнозначность элементов геометрии, было первым качественным отображением на плоскости факторов напряженности пространства и свидетельствовало о другом ранге несобственных точек. Однако нарушения равнозначности элементов обнаружено не было, и не потому, что оно отсутствует, а потому, что и обычным, и несобственным точкам и площадям постулировали равноправие. Это постулирование равноправия обусловило полную статичность проективной геометрии, снивилировало напряженности, привело к тому, что все прямые одной плоскости Дезарга всегда пересекаются на бесконечности. Таким образом, вопрос о различной напряженности у точек и линий на плоскости даже не возник. Развитие получили аксиомы статической геометрии.

Если, для примера, представить движение колес паровоза по рельсам в обычном пространстве несобственной (потенциальной бесконечности), то мы увидим, как бы следуя за ним неизменными, что рельсы сначала будут параллельными (расстояние между ними - образующий луч, остается неизменным). Затем под воздействием возрастающей напряженности несобственного пространства рельсы как бы начнут сходиться (образующий луч будет уменьшаться и, соответственно паровоз тоже). И, подойдя к несобственной точке, луч станет по «длине» меньше ее. Пройдя поверхность сферы-точки, т.е. проникнув в объем другого ранга, луч продолжает уменьшаться и, миновав центр (но не через него), начинает возрастать до противоположной поверхности сферы. Поскольку напряженность поверхности вокруг точки сферически симметрична (в предположении, что точка находится вдали от других точек), по выходу из несобственной точки луч начнет расширяться, а рельсы, следовательно, расходиться под тем же самым углом, под которым они сходились. В результате возникнет полная иллюзия того, что в несобственной точке произошло пересечение рельсов. На самом деле, на всем протяжении движения к точке, сквозь нее и за ней рельсы оставались параллельными. Менялась же напряженность несобственного пространства и несобственной точки в полном соответствии с динамикой пространства, что и создавало иллюзию схождения и расхождения рельсов. (Их пересечения в одной точке.)

Вторично неявная напряженность геометрической поверхности проявила себя в геометриях Лобачевского и Римана. Это станет особенно заметно, если луч Л, входящий в точку М из прямой а, начинает двигаться вместе с точкой М на бесконечность, например в правую сторону (рис. 40.). Причем граничные условия аксиомы запрещают точке приближение к прямой а, а лучу - сокращаться по длине, но не запрещают точке М удаляться, а лучу Л удлиняться (своего рода пространственное отталкивание). Поэтому по мере движения точка начинает отклоняться от прямой - ветвь в¢. Если же луч Л вместе с точкой будет двигаться в левую сторону, то получим аналогичное отклонение от прямой а, - ветвь в. Фигура, образуемая обеими ветвями как бы единой прямой в, окажется не эквидистантой, а некоторой седловиной.

В этом построении начинает проявляться физический смысл движения, и точка М замыкает на себя две самостоятельные ветви прямой в, разрывая ее и имея статус несобственной точки (точки одного ранга с прямой). Отсюда также следует, что пространство, в котором двигаются «прямые», анизотропно. А потому луч Л, двигаясь от точки в любую из сторон, будет изменять свою длину пропорционально изменению напряженности пространства и движущейся точки. И также пропорционально этой напряженности будет меняться метричность отрезков по длине прямой вМв¢.

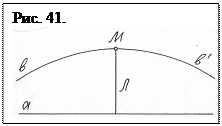
Если же граничные условия (по Риману) препятствуют отклонению ветвей в и в¢ от прямой а, при движении в обе стороны от точки М, то ветви в и в ', перемещаясь на бесконечность, будут приближаться к прямой а (рис. 41.). Таким образом, граничные условия не позволяют образующему лучу в движении удлиняться, оставляя ему возможность сокращения. И в этих условиях луч Л выписывает подобие эллиптической кривой (своего рода про­странственное притяжение). Однако конечные точки ветвей в и в¢, имеющие ранг прямой, никогда не пересекут прямую а. И кривая вМв¢ никогда не будет иметь общей точки с прямой а. Она не замкнута.

Подобие линии вМв¢ эллиптической кривой послужило основанием для наречения римановой геометрии сферической. Оно завуалировало и существование напряженности пространства, и разрыв кривой в точке М. Сферическая поверхность, образованная данной кривой при вращении ее вокруг а, как уже говорилось, не может считаться истинной сферой. И потому, что след точки М несет в себе момент нестыковки ветвей в и в¢. И потому, что эта "сфера" оказывается незамкнутой с линией а. И потому, что внутри "сферы" остается элемент образующей ее структуры - прямая а.

Напряженность, выражаемая элементами геометрии в виде неравноправных, несобственных точек и линий, по-видимому, снимается введением в геометрию понятия абсолюта - такой геометрической фигуры, которая остается неизменной при любых преобразованиях данной подгруппы. Следовательно, абсолютом считается элемент, ранг собственной напряженности которого выше остальных элементов данной плоскости. И все преобразования, изменяющие форму остальных элементов (и их напряженность), не в состоянии изменить напряженность абсолюта.

Таким образом, понятие абсолюта окончательно закрыло в геометрии все направления возможного описания реального мира в терминах напряженности, движения, взаимодействия. Геометрия превратилась в чисто статическое описание только одной актуальной бесконечности.

Попробуем в самой эскизной форме резюмировать некоторые первичные понятия и свойства элементов динамического пространства. Прежде всего, отметим важнейшую роль познания потенциальной бесконечности. Бесконечность как понятие - высшая форма абстрагирования. Представление об осуществимости абстрактного движения в бесконечность приводит к противоречию с проявлением неопределенности и недостижимости в отдалении от нашего сознания. Движение в бесконечность оказывается абстракцией, связанной с возможностями качественного изменения дискретного пространства с переходом от пространства одного ранга к пространству другого ранга. Именно ранжирование бесконечностей по уровням определяет соизмеримость или несоизмеримость пространственных образований или отрезков прямых.

Иерархическая равнозначность ранговых структур по их положению и естественное взаимодействие при движении определяет дискретность и непрерывность образуемого ячейками пространства плоскости или объема. Ячеистое поле пространства само для себя и для своего ранга дискретно, а для верхнего ранга непрерывно и носит полевой характер. Динамическое пространство всегда не пусто.

Естественный смысл бесконечности заключается в ее количественной и качественной незавершенности. Это выражается, в частности, через изменение метричности в сопоставлении с метричностью статической геометрии. Каждый последующий шаг всегда отличен от предыдущего качественно и количественно.

Как только вводится понятие бесконечного пространства, и элементы геометрических фигур устремляются в бесконечность (пятая аксиома в формулировке Евклида), тем самым вводятся новые, ей не присущие качества и в статическую геометрию (движение, недостижимость бесконечности, неопределенность, время, взаимодействие и т.д.). И эти качества коренным образом изменяют поведение геометрических элементов и пространства, которое описывается ими. Эти качества приводят к взаимосвязи всех элементов движения и геометрическая статическая общность точек, отрезков, плоскостей, объемов сразу наполняется физическим содержанием и становится разделом физики, системной общностью. Общностью, в которой ни одна точка, ни одна фигура, ни в одном месте пространства не обладает истинной самостоятельностью, оставаясь в то же время равновеликой по значимости и взаимодействию со всеми фигурами и пространством. И всякое ее движение в любом направлении этого пространства будет сопровождаться изменением ее геометрических (статических) параметров пропорционально напряженности самого пространства. Однако динамические (физические) параметры этой общности останутся неизменными. И эти качественные противоречия изменяемости и неизменности параметров в статическом и динамическом состояниях тоже неявно заложены в аксиому о параллельных.

Перенос отрезков или фигур параллельно своему положению вдоль замкнутого контура вызывает их постоянное самотождественное изменение, но в результате обхода контура конечная фигура совпадет с первичной фигурой. В пространстве отсутствуют малые поверхности и объемы (относительно измерителя), и перенос фигуры или мерного инструмента из одного пространства в другое вызывает изменение длины мерных инструментов (относительно статики) пропорционально напряженности внешнего поля данного пространства. Сумма же углов треугольника и на поверхности сферы, и в объеме всегда равна 2p.

Отличительная особенность динамического пространства является детерминизм последовательного изменения фигур. Именно каузальность порядка причина-следствие определяется коэффициентом связности и золотым многообразием.

Рассмотрим основные фигуры пространства. Все материальные образования одного ранга, кроме продуктов катастроф, стремятся приобрести форму сферы. Сферы одного пространства обладают следующими качествами:

- все сферы, построенные вокруг отсутствующего единого центра, по объему равны между собой. Их эквипотенциальная поверхность состоит из бесчисленного количества ячеек, а радиус имеет бесконечную длину;

- каждый отрезок исходит из точки и входит в другую точку. Однако их можно продолжить по прямолинейной поверхности сферы до исходя­щего отрезка и считать непрерывными;

- все окружности, построенные на сфере, по длине равны;

- сферы всегда ядра и на плоскости и в пространстве различаются по рангу. Сферы более «низкого» ранга могут считаться точками. Точка - это всегда материальная сфера, не имеющая центра.

Точка - ядро, структура которого несоизмерима по рангу с пространством, вкотором она находится, и влияющая на него. Внешняя поверхность отграничивает ее от пространства. Точка всегда бесконечна вглубь. Точка на прямой или в пространстве и луч из нее - это отделение соизмеримой области пространства (внешняя часть образующегося луча) от несоизмеримой (части, устремленной к центру точки).

Все точки одного ранга неравнозначны по количественным величинам всех качеств и в первую очередь по напряженности. Поэтому метрика координатных осей с центром в любой окрестности точки, кроме ядра, будет различной (относительно статического эталонного метра).

Ячейка (две или более) - взаимосвязанные напряженностью собственного поля сферические структуры (ядра), несоизмеримые по размерам с расстояниями между ними, входящие в единую внешнюю эквипотенциальную, нейтральную зону. Все пространство - «пена» взаимосвязанных первичных ячеек.

Линия (прямая) - абстракция - последовательность расположенных в одном направлении несоизмеримых с пространством ячеек. Линия всегда дискретна. Дискретность обусловлена наличием бесконечных (вглубь) точек на ней. Непрерывной она может быть только мысленно.

Поверхность (плоскость) - многообразие распространяющихся в двух направлениях дискретных ячеек.

Объем - область, образованная состоянием взаимосвязанных ячеек, отграниченная от других областей своей нейтральной зоной. Существование нейтральных зон определенной напряженности обусловливает свойства каждого из тел.

 

 

Глава III.

 

Золотые пропорции геометрии

 

⇐ Предыдущая10111213141516171819Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: