 |
Уравнение прямой, проходящей через две точки
|
|
|
|
Определение смешанного произведения.
Смешанное произведение определяется для трех векторов, заданных в трехмерном пространстве.
Определение.
Смешанным произведением трех векторов 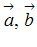 и
и 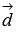 называется действительное число, равное скалярному произведению векторов
называется действительное число, равное скалярному произведению векторов  и
и 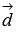 , где
, где  - векторное произведение векторов
- векторное произведение векторов 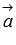 и
и  .
.
Из определения понятно, почему смешанное произведение часто называют векторно-скалярным произведением.
Смешанное произведение векторов 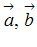 и
и 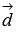 обычно обозначают
обычно обозначают  . В таких обозначениях по определению смешанного произведения
. В таких обозначениях по определению смешанного произведения 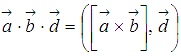 .
.
Уравнение прямой на плоскости.
Пусть на плоскости зафиксирована прямоугольная декартова система координат Oxy и в ней задана прямая линия.
Прямая, как и любая другая геометрическая фигура, состоит из точек. В фиксированной прямоугольной системе координат каждая точка прямой имеет свои координаты – абсциссу и ординату. Так вот зависимость между абсциссой и ординатой каждой точки прямой в фиксированной системе координат, может быть задана уравнением, которое называют уравнением прямой на плоскости.
Другими словами, уравнение прямой на плоскости в прямоугольной системе координат Oxy есть некоторое уравнение с двумя переменными x и y, которое обращается в тождество при подстановке в него координат любой точки этой прямой.
Осталось разобраться с вопросом, какой вид имеет уравнение прямой на плоскости. Ответ на него содержится в следующем пункте статьи. Забегая вперед, отметим, что существуют различные формы записи уравнения прямой, что объясняется спецификой решаемых задач и способом задания прямой линии на плоскости. Итак, приступим к обзору основных видов уравнения прямой линии на плоскости.
|
|
|
Общее уравнение прямой.
Вид уравнения прямой в прямоугольной системе координат Oxy на плоскости задает следующая теорема.
Теорема.
Всякое уравнение первой степени с двумя переменными x и y вида 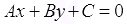 , где А, В и С – некоторые действительные числа, причем А и В одновременно не равны нулю, задает прямую линию в прямоугольной системе координат Oxy на плоскости, и всякая прямая на плоскости задается уравнением вида
, где А, В и С – некоторые действительные числа, причем А и В одновременно не равны нулю, задает прямую линию в прямоугольной системе координат Oxy на плоскости, и всякая прямая на плоскости задается уравнением вида 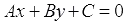 .
.
Уравнение 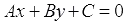 называется общим уравнением прямой на плоскости.
называется общим уравнением прямой на плоскости.
Поясним смысл теоремы.
Заданному уравнению вида 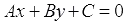 соответствует прямая на плоскости в данной системе координат, а прямой линии на плоскости в данной системе координат соответствует уравнение прямой вида
соответствует прямая на плоскости в данной системе координат, а прямой линии на плоскости в данной системе координат соответствует уравнение прямой вида 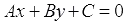 .
.
Посмотрите на чертеж.
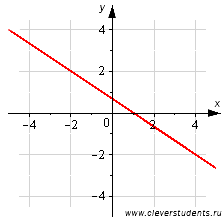
С одной стороны можно сказать, что эта линия определяется общим уравнением прямой вида 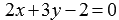 , так как координаты любой точки изображенной прямой удовлетворяют этому уравнению. С другой стороны, множество точек плоскости, определяемых уравнением
, так как координаты любой точки изображенной прямой удовлетворяют этому уравнению. С другой стороны, множество точек плоскости, определяемых уравнением 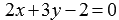 , дают нам прямую линию, приведенную на чертеже.
, дают нам прямую линию, приведенную на чертеже.
Общее уравнение прямой называется полным, если все числа А, В и С отличны от нуля, в противном случае общее уравнение прямой называется неполным. Неполное уравнение прямой вида 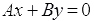 определяют прямую, проходящую через начало координат. При А=0 уравнение
определяют прямую, проходящую через начало координат. При А=0 уравнение 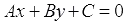 задает прямую, параллельную оси абсцисс Ox, а при В=0 – параллельную оси ординат Oy.
задает прямую, параллельную оси абсцисс Ox, а при В=0 – параллельную оси ординат Oy.
Таким образом, любую прямую на плоскости в заданной прямоугольной системе координат Oxy можно описать с помощью общего уравнения прямой при некотором наборе значений чисел А, В и С.
Нормальный вектор прямой, заданной общим уравнением прямой вида 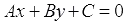 , имеет координаты
, имеет координаты 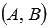 .
.
Все уравнения прямых, которые приведены в следующих пунктах этой статьи, могут быть получены из общего уравнения прямой, а также могут быть обратно приведены к общему уравнению прямой.
Рекомендуем к дальнейшему изучению статью общее уравнение прямой. Там доказана теорема, сформулированная в начале этого пункта статьи, приведены графические иллюстрации, подробно разобраны решения примеров на составление общего уравнения прямой, показан переход от общего уравнения прямой к уравнениям другого вида и обратно, а также рассмотрены другие характерные задачи.
|
|
|
Уравнение прямой, проходящей через две точки
Пусть в пространстве заданы две точки M 1 (x 1, y 1, z 1) и M2 (x 2, y 2, z 2), тогда уравнение прямой, проходящей через эти точки:

Если какой-либо из знаменателей равен нулю, следует приравнять нулю соответствующий числитель.На плоскости записанное выше уравнение прямой упрощается:
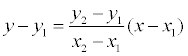
если х 1 ≠ х2 и х = х 1, если х 1 = х2.
Дробь 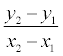 = k называется угловым коэффициентом прямой.
= k называется угловым коэффициентом прямой.
Пример. Найти уравнение прямой, проходящей через точки А(1, 2) и В(3, 4).
Решение. Применяя записанную выше формулу, получаем:

5. Уравнение прямой, проходящей через данную точку в данном направлении
Выведем уравнение прямой, проходящей через данную точку A(x1;y1) и имеющей данный угловой коэффициент k. Уравнение этой прямой имеет вид:
1. y=kx+в (5)
Так как искомая прямая проходит через точку A(x1;y1), то координаты этой точки должны удовлетворять уравнению (5):
2. y1=kx1+в (6)
Из уравнения (6) выражаем в=y1-kx1 и подставляем в уравнение (5):
y-y1=k(x-x1)
Это и есть уравнение искомой прямой. Уравнение прямой, проходящей через данную точку A(x1;y1) параллельно оси Oу, будет иметь вид: x=x1
Пример 3. Составить уравнение прямой, проходящей через точку (-3;4) и наклоненную к оси Oх под углом в 135°
Уравнение прямой можно записать в форме (7). Здесь x1=-3, y1=4, k=tg135°=-1
Следовательно, искомое уравнение будет у-4=-1(х+3), или х+у-1=0.
|
|
|


