Удаление скрытых линий и поверхностей

ПРОЕКЦИИ

Введение

Методические указания составлены на основе работ [1-3]. В разделе 1 рассматриваются параллельные, перспективные и стереопроекции; плоские преобразования растровых картин.

При визуализации двумерных изображений достаточно задать окно видимости в системе координат пользователя и порт отображения на экране дисплея, в котором будет выдаваться изображение из окна. В этом случае достаточно провести отсечение изображения по окну и выполнить двумерные преобразования окно-порт. На рис. 1.1. показан простой пример двумерных преобразований. Окном отсекается часть изображения домика и один улей (см. рис. 1.1. слева). Отсеченное изображение передается в порт отображения дисплея с выполнением преобразований окно-порт (см. рис. 1.1. справа). В данном (простом) случае выполняется только преобразование сдвига.

В случае же трехмерных изображений отсечение выполняется уже не по окну, а по объему видимости и затем выполняется проецирование в порт отображения, который в свою очередь может быть проекцией объема видимости. Модель процесса визуализации трехмерных изображений приведена на рис. 1.2..

Проецирование в общем случае - отображение точек, заданных в системе координат размерностью N, в точки в системе с меньшей размерностью. При отображении трехмерных изображений на дисплей три измерения отображаются в два.

Проецирование выполняется с помощью прямолинейных проекторов (проецирующих лучей), идущих из центра проекции через каждую точку объекта до пересечения с картинной поверхностью (поверхностью проекции). Далее рассматриваются только плоские проекции, при которых поверхность проекции - плоскость в трехмерном пространстве.

По расположению центра проекции относительно плоскости проекции различаются центральная и параллельные проекции.

При параллельной проекции центр проекции находится на бесконечном расстоянии от плоскости проекции. Проекторы представляют собой пучок параллельных лучей. В этом случае необходимо задавать направление проецирования и расположение плоскости проекции. По взаимному расположению проекторов, плоскости проекции и главных осей координат различаются ортогональные, прямоугольные аксонометрические и косоугольные аксонометрические проекции.

При ортогональной проекции проекторы перпендикулярны плоскости проекции, а плоскость проекции перпендикулярна главной оси. Т.е. проекторы параллельны главной оси.

При аксонометрической проекции имеется одна из двух перпендикулярностей:

· при прямоугольной аксонометрической проекции проекторы перпендикулярны плоскости проекции, которая расположена под углом к главной оси;

· при косоугольной аксонометрической проекции проекторы не перпендикулярны плоскости проекции, но плоскость проекции перпендикулярна к главной оси.

Изображение, полученное при параллельном проецировании, не достаточно реалистично, но передаются точные форма и размеры, хотя и возможно различное укорачивание для различных осей.

При центральной проекции расстояние от центра проекции до плоскости проецирования конечно, поэтому проекторы представляют собой пучок лучей, исходящих из центра проекции. В этом случае надо задавать расположение и центра проекции и плоскости проекции. Изображения на плоскости проекции имеют т.н. перспективные искажения, когда размер видимого изображения зависит от взаимного расположения центра проекции, объекта и плоскости проекции. Из-за перспективных искажений изображения, полученные центральной проекцией, более реалистичны, но нельзя точно передать форму и размеры.

Различаются одно, двух и трехточечные центральные проекции в зависимости от того по скольким осям выполняется перспективное искажение.

На рис. 1.3. приведена классификация описанных выше плоских проекций.

1.2. Параллельные проекции

Вначале мы рассмотрим ортогональные проекции, используемые в техническом черчении, в регламентированной для него правосторонней системе координат, когда ось Z изображается вертикальной. Затем будут проиллюстрированы аксонометрические проекции также в правосторонней системе координат, но уже более близкой к машинной графике (ось Y вертикальна, ось X направлена горизонтально вправо, а ось Z - от экрана к наблюдателю). Наконец выведем матрицы преобразования в левосторонней системе координат, часто используемой в машинной графике, с вертикальной осью Y, осью X, направленной вправо и осью Z, направленной от наблюдателя.

Использование проекций в техническом черчении регламентируется стандартом ГОСТ 2.317-69. Наиболее широко, особенно, в САПР используются ортогональные проекции (виды). Вид - ортогональная проекция обращенной к наблюдателю видимой части поверхности предмета, расположенного между наблюдателем и плоскостью чертежа.

В техническом черчении за основные плоскости проекций принимают шесть граней куба (рис. 1.4.).

На рисунке обозначены:

1. Вид спереди, главный вид, фронтальная проекция, (на заднюю грань V),

2. Вид сверху, план, горизонтальная проекция, (на нижнюю грань H),

3. Вид слева, профильная проекция, (на правую грань W),

4. Вид справа (на левую грань),

5. Вид снизу (на верхнюю грань),

6. Вид сзади (на переднюю грань).

Очевидно, что при ортогональной проекции не происходит изменения ни углов, ни масштабов.

При аксонометрическом проецировании (см. рис. 1.4.) сохраняется параллельность прямых, а углы изменяются; измерение же расстояний вдоль каждой из координатных осей в общем случае должно выполняться со своим масштабным коэффициентом.

При изометрических проекциях укорачивания вдоль всех координатных осей одинаковы, поэтому можно производить измерения вдоль направлений осей с одним и тем же масштабом (отсюда и название изометрия). На рис. 1.4. приведена (аксонометрическая прямоугольная) изометрическая проекция куба со стороной A. При этой проекции плоскость проецирования наклонена ко всем главным координатным осям под одинаковым углом. Стандартом регламентируется коэффициент сжатия, равный 0.82, а также расположение и взаимные углы главных координатных осей, равные 120⁰ как это показано в левом верхнем углу рис. 1.4.. Обычно сжатие не делается.

При диметрической проекции две из трех осей сокращены одинаково, т.е. из трех углов между нормалью к плоскости проекции и главными координатными осями два угла одинаковы. На рис. 1.5. приведена (аксонометрическая прямоугольная) диметрическая проекция куба со стороной A. Там же показаны регламентируемые расположение осей и коэффициенты сжатия. Обычно вместо коэффициента сжатия 0.94 используется 1, а вместо 0.47 - 0.5.

В косоугольных проекциях плоскость проекции перпендикулярна главной координатной оси, а проекторы расположены под углом к ней. Таким образом, аксонометрические косоугольные проекции сочетают в себе свойства ортогональных и аксонометрических прямоугольных проекций.

Наиболее употребимы два вида косоугольной проекции - фронтальная (косоугольная) диметрия (проекция Kabinett - кабине) и горизонтальная (косоугольная) изометрия (проекция Kavalier - кавалье) или военная перспектива.

В случае фронтальной (косоугольной) диметрии при использовании правосторонней системы координат экрана плоскость проецирования перпендикулярна оси Z. Ось X направлена горизонтально вправо. Ось Z изображается по углом в 45⁰ относительно горизонтального направления. Допускается угол наклона в 30 и 60⁰. При этом отрезки, перпендикулярные плоскости проекции, при проецирования сокращаются до 1/2 их истинной длины. На рис.1.6. приведена (аксонометрическая косоугольная) фронтальная диметрическая проекция куба со стороной A, там же показаны регламентируемые коэффициент сжатия, равный 0.5 и расположение осей.

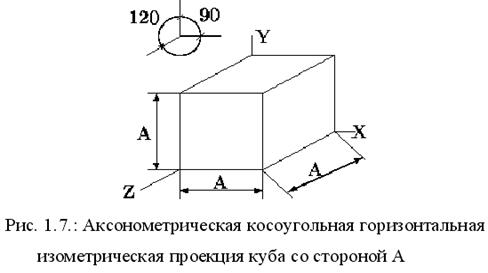
В случае же (аксонометрической косоугольной) горизонтальной изометрии, как следует из названия, плоскость проецирования перпендикулярна оси Y а укорачивания по всем осям одинаковы и равны 1. Угол поворота изображения оси X относительно горизонтального направления составляет 30⁰. Допускается 45 и 60⁰ при сохранении угла 90⁰ между изображениями осей X и Z. Иллюстрация этого приведена на рис.1.7.

Выведем выражения для матриц преобразования, используя теперь левостороннюю систему координат более естественную для машинной графики.

Простейшее параллельное проецирование - ортогональное выполняется на плоскость, перпендикулярную какой-либо оси, т.е. при направлении проецирования вдоль этой оси. В частности, проецирование в XY-плоскость, заданную соотношением Z = Z₀, выполняется следующим образом:

Рассмотрим теперь косоугольное проецирование, при котором плоскость проецирования перпендикулярна главной оси, а проекторы составляют с плоскостью проецирования угол не равный 90⁰. Матрица для этого преобразования может быть найдена исходя из значений угла проецирования и координат преобразованной точки. На рис. 1.8. показана косоугольная параллельная проекция единичного куба.

Из рисунка видно, что проектором, идущим из точки P₀ в P₁, точка P₀(0,0,1) проецируется в P₁(L·cosa, L·sina, 0).

Теперь проектором, параллельным рассмотренному (рис.1.8.), спроецируем некоторую точку (X,Y,Z) в точку (X_p,Y_p,Z_p).

Из подобия треугольников получаем:

Это соответствует следующему матричному выражению:

Таким образом, матрица аксонометрической косоугольной проекции для случая проецирования в плоскость Z = 0, выполняет следующее:

· вначале плоскости с заданной координатой Z₀ переносятся вдоль оси X на Z₀·L·cos и вдоль оси Y на Z₀·L·sin ,

· затем производится проецирование в плоскость Z = 0.

Различные варианты параллельных проекций формируются из полученной подстановкой значений L и углов и 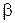(см. рис. 1.8.). В частности, для фронтальной косоугольной диметрии L = 1/2, следовательно, угол 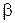между проекторами и плоскостью проецирования равен arctan2 = 63.4⁰. Угол же , равен 45⁰ и допускается 30 и 60⁰, как это сказано выше. (Обратите внимание, что в этой системе координат плоскость фронтальной проекции - плоскость XY, в отличие от системы координат технического черчения, где фронтальная проекция, как это показано на рис. 1.4., формируется в плоскости XZ).

1.3. Центральная проекция

Наиболее реалистично трехмерные объекты выглядят в центральной проекции из-за перспективных искажений сцены. Центральные проекции параллельных прямых, не параллельных плоскости проекции будут сходиться в точке схода. В зависимости от числа точек схода, т.е. от числа координатных осей, которые пересекает плоскость проекции, различаются одно, двух и трехточечные центральные проекции. Иллюстрация одно-, двух- и трехточечной центральных проекций куба приведена на рис. 1.10..

Наиболее широко используется двухточечная центральная проекция.

Выведем матрицу, определяющую центральное проецирование для простого случая одноточечной проекции (рис. 1.11), когда плоскость проекции перпендикулярна оси Z и расположена на расстоянии d от начала координат. (Здесь используется удобная для машинной графики левосторонняя система координат).

Начало отсчета находится в точке просмотра. Ясно, что изображения объектов, находящиеся между началом координат и плоскостью проекции увеличиваются, а изображения объектов, расположенных дальше от начала координат, чем плоскость проекции уменьшаются.

Из рис. 1.11. видно, что для координат (X1,Y1) точки P₁, полученной проецированием точки P₀(X,Y,Z) в плоскость Z = d (плоскость экрана) выполняются следующие соотношения:

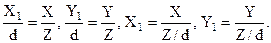
Такое преобразование может быть представлено матрицей 4×4

Для перехода к декартовым координатам делим все на z/d и получаем:

Если же точка просмотра расположена в плоскости проекции, тогда центр проекции расположен в точке (0,0,-d). Рассматривая подобные треугольники, аналогично вышеописанному, можем получить:

Матрица преобразования в этом случае имеет вид:

Матрица M₀ может быть представлена в виде:

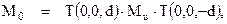
т.е. преобразование проецирования выполняется для этого случая путем переноса начала координат в центр проецирования, собственно проецирования и обратного сдвига начала координат.

ГЕНЕРАЦИЯ ВЕКТОРОВ

2.1. Введение

Назначение генератора векторов - соединение двух точек изображения отрезком прямой.

Далее будет рассмотрен алгоритм Брезенхема для генерации векторов;

Перед рассмотрением алгоритма сформулируем общие требования к изображению отрезка:

 концы отрезка должны находиться в заданных точках;

 отрезки должны выглядеть прямыми,

 яркость вдоль отрезка должна быть постоянной и не зависеть от длины и наклона.

Ни одно из этих условий не может быть точно выполнено на растровом дисплее в силу того, что изображение строится из пикселей конечных размеров, а именно:

 концы отрезка в общем случае располагаются на пикселях, лишь наиболее близких к требуемым позициям и только в частных случаях координаты концов отрезка точно совпадают с координатами пикселей;

 отрезок аппроксимируется набором пикселей и лишь в частных случаях вертикальных, горизонтальных и отрезков под 45⁰ они будут выглядеть прямыми, причем гладкими прямыми, без ступенек только для вертикальных и горизонтальных отрезков (рис. 2.1);

 яркость для различных отрезков и даже вдоль отрезка в общем случае различна, так как, например, расстояние между центрами пикселей для вертикального отрезка и отрезка под 45⁰ различно (см. рис. 2.1.).

Объективное улучшение аппроксимации достигается увеличением разрешения дисплея, но в силу существенных технологических проблем для растровых систем приемлемой скорости разрешение составляет порядка 1280×1024.

Субъективное улучшение аппроксимации основано на психофизиологических особенностях зрения и, в частности, может достигаться просто уменьшением размеров экрана. Другие способы субъективного улучшения качества аппроксимации основаны на различных программных ухищрениях по "размыванию" резких границ изображения.

Далее в этом разделе рассмотрен один из алгоритмов генерации отрезка.

2.2. Алгоритм Брезенхема

Брезенхем предложил алгоритм, обеспечивающий минимизацию отклонения сгенерированного образа от истинного отрезка. Основная идея алгоритма состоит в том, что если угловой коэффициент прямой < 1/2, то естественно точку, следующую за точкой (0,0), поставить в позицию (1,0) (рис. 2.2.а), а если угловой коэффициент > 1/2, то - в позицию (1,1) (рис. 2.2.б). Для принятия решения куда заносить очередной пиксель вводится величина отклонения Е точной позиции от середины между двумя возможными растровыми точками в направлении наименьшей относительной координаты. Знак Е используется как критерий для выбора ближайшей растровой точки.

Если Е < 0, то точное Y-значение округляется до последнего меньшего целочисленного значения Y, т.е. Y-координата не меняется по сравнению с предыдущей точкой. В противном случае Y увеличивается на 1.

Для вычисления Е без ограничения общности для упрощения положим, что рассматриваемый вектор начинается в точке (0,0) и проходит через точку (4,1.5) (см. рис. 2.2в), т.е. имеет положительный наклон меньший 1. Из рис. 2.2.в видно, отклонение для первого шага:

где P_y = Y_k – Y_n - приращение координат отрезка по оси Y, а P_x = X_k – X_n - приращение координат отрезка по оси X, поэтому для занесения пикселя выбирается точка (1,0).

Отклонение для второго шага вычисляется добавлением приращения Y-координаты для следующей X-позиции (см. рис.2.2.в):

поэтому для занесения пикселя выбирается точка (2,1). Так как отклонение считается от Y-координаты, которая теперь увеличилась на 1, то из накопленного отклонения для вычисления последующих отклонений надо вычесть 1:

Отклонение для третьего шага:

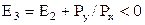
поэтому для занесения пикселя выбирается точка (3,1).

Суммируя и обозначая большими буквами растровые точки, а маленькими - точки вектора, получаем:

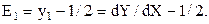
Возможны случаи: E₁>0 или E₁ 0, ближайшая точка есть:

Так как интересует только знак Е, то можно избавиться от неудобных частных умножением E на 2×P_x:

ГЕНЕРАЦИЯ ОКРУЖНОСТИ

3.1. Введение

Во многих областях приложений, таких как, например, системы автоматизированного проектирования машиностроительного направления, естественными графическими примитивами, кроме отрезков прямых и строк текстов, являются и конические сечения, т.е. окружности, эллипсы, параболы и гиперболы. Наиболее употребительным примитивом, естественно, является окружность. Один из наиболее простых и эффективных алгоритмов генерации окружности разработан Брезенхемом.

3.2. Алгоритм Брезенхема

Для простоты и без ограничения общности рассмотрим генерацию 1/8 окружности, центр которой лежит в начале координат. Остальные части окружности могут быть получены последовательными отражениями (использованием симметрии точек на окружности относительно центра и осей координат).

Окружность с центром в начале координат описывается уравнением:

Алгоритм Брезенхема пошагово генерирует очередные точки окружности, выбирая на каждом шаге для занесения пикселя точку растра P_i(X_i,Y_i), ближайшую к истинной окружности, так чтобы ошибка:

была минимальной. Причем, как и в алгоритме Брезенхема для генерации отрезков, выбор ближайшей точки выполняется с помощью анализа значений управляющих переменных, для вычисления которых не требуется вещественной арифметики. Для выбора очередной точки достаточно проанализировать знаки.

Рассмотрим генерацию 1/8 окружности по часовой стрелке, начиная от точки X=0, Y=R.

Проанализируем возможные варианты занесения i+1-й точки, после занесения i-й.

При генерации окружности по часовой стрелке после занесения точки (X_i, Y_i) следующая точка может быть (см. рис.3.1.а) либо P_g = (X_i+1, Y_i) - перемещение по горизонтали, либо P_d = (X_i+1, Y_i-1) - перемещение по диагонали, либо P_v = (X_i, Y_i-1) - перемещение по вертикали.

Для этих возможных точек вычислим и сравним абсолютные значения разностей квадратов расстояний от центра окружности до точки и окружности:

Выбирается и заносится та точка, для которой это значение минимально.

Выбор способа расчета определяется по значению D_d. Если D_d < 0, то диагональная точка внутри окружности. Это варианты 1-3 (см. рис. 3.1. б). Если D_d > 0, то диагональная точка вне окружности. Это варианты 5-7. И, наконец, если D_d = 0, то диагональная точка лежит точно на окружности. Это вариант 4. Рассмотрим случаи различных значений D_d в только что приведенной последовательности.

Случай D_d < 0

Здесь в качестве следующего пикселя могут быть выбраны или горизонтальный - P_g или диагональный - P_d.

Для определения того, какой пиксель выбрать P_g или P_d составим разность:

И будем выбирать точку P_g при d_i 0, в противном случае выберем P_d.

Рассмотрим вычисление d_i для разных вариантов.

Для вариантов 2 и 3:

D_g 0 и D_d < 0, так как горизонтальный пиксель либо вне, либо на окружности, а диагональный внутри.

di = (X+1)2 + Y2 - R2 + (X+1)2 + (Y-1)2 - R2;

Добавив и вычтя (Y-1)² получим:

di = 2 ·[(X+1)2 + (Y-1)2 - R2] + 2·Y - 1

В квадратных скобках стоит D_d, так что

di = 2 ·(Dd + Y) - 1

Для варианта 1:

Ясно, что должен быть выбран горизонтальный пиксель P_g. Проверка компонент d_i показывает, что D_g < 0 и D_d < 0, причем d_i < 0, так как диагональная точка больше удалена от окружности, т.е. по критерию d_i < 0 как и в предыдущих случаях следует выбрать горизонтальный пиксель P_g, что верно.

Случай D_d > 0

Здесь в качестве следующего пикселя могут быть выбраны или диагональный - P_d или вертикальный P_v.

Для определения того, какой пиксель выбрать P_d или P_v составим разность:

Если s_i 0, то расстояние до вертикальной точки больше и надо выбирать диагональный пиксель P_d, если же s_i > 0, то выбираем вертикальный пиксель P_v.

Рассмотрим вычисление s_i для разных вариантов.

Для вариантов 5 и 6:

D_d > 0 и D_v 0, так как диагональный пиксель вне, а вертикальный либо вне либо на окружности.

si = (X+1)2 + (Y-1)2 - R2 + X2 + (Y-1)2 - R2;

Добавив и вычтя (X+1)² получим:

si = 2 ·[(X+1)2 + (Y-1)2 - R2] - 2·X - 1

В квадратных скобках стоит D_d, так что

si = 2 ·(Dd - X) - 1

Для варианта 7:

Ясно, что должен быть выбран вертикальный пиксель P_v. Проверка компонент s_i показывает, что D_d > 0 и D_v > 0, причем s_i > 0, так как диагональная точка больше удалена от окружности, т.е. по критерию s_i > 0 как и в предыдущих случаях следует выбрать вертикальный пиксель P_v, что соответствует выбору для вариантов 5 и 6.

Случай D_d = 0

Для компонент d_i имеем: D_g > 0 и D_d = 0, следовательно по критерию d_i > 0 выбираем диагональный пиксель.

С другой стороны, для компонент s_i имеем: D_d = 0 и D_v < 0, так что по критерию s_i 0 также выбираем диагональный пиксель.

Итак:

D_d < 0

d_i 0 - выбор горизонтального пикселя P_g

d_i > 0 - выбор диагонального пикселя P_d

D_d > 0

s_i 0 - выбор диагонального пикселя P_d

s_i > 0 - выбор вертикального пикселя P_v

D_d = 0

выбор диагонального пикселя P_d.

Выведем рекуррентные соотношения для вычисления D_d для (i+1)-го шага, после выполнения i-го.

1. Для горизонтального шага к X_i+1, Y_i

X_i+1=X_i+1
Y_i+1=Y_i
D_di=(X_i+1+1)²+(Y_i+1-1)²-R²=X_i+1²+2·X_i+1+1+(Y_i+1-1)²-R²=
(X_i+1)²+(Y_i-1)²-R²+2·X_i+1+1=D_{d i} + 2·X_i+1 + 1

2. Для диагонального шага к X_i+1, Y_i-1

X_i+1=X_i+1
Y_i+1=Y_i-1
D_{d i+1} = D_{d i} + 2 ·X_i+1 - 2 ·Y_i+1 + 2

3. Для вертикального шага к X_i, Y_i-1

X_i+1=X_i
Y_i+1=Y_i-1
D_{d i+1} = D_{d i} - 2 ·Y_i+1 + 1

Начальная инициализация должна быть:

X= 0

Y= R

D_d = (X+1)² + (Y-1)² - R² = 1 + (R-1)² - R² = 2*(1 - R)

Пиксели в остальных четвертях можно получить отражением. Кроме того достаточно сформировать дугу только во втором октанте, а остальные пиксели сформировать из соображений симметрии.

Остальная часть окружности строится симметрично.

ЗАПОЛНЕНИЕ МНОГОУГОЛЬНИКА

4.1. Введение

В большинстве приложений используется одно из существенных достоинств растровых устройств - возможность заполнения областей экрана.

Существует две разновидности заполнения:

i первая, связанная как с интерактивной работой, так и с программным синтезом изображения, служит для заполнения внутренней части многоугольника, заданного координатами его вершин.

i вторая, связанная в первую очередь с интерактивной работой, служит для заливки области, которая либо очерчена границей с кодом пикселя, отличающимся от кодов любых пикселей внутри области, либо закрашена пикселями с заданным кодом;

4.2. Заполнение многоугольника

В данном разделе рассмотрим алгоритм заполнения многоугольника. В следующем разделе будут рассмотрены алгоритмы заливки области.

Простейший способ заполнения многоугольника, заданного координатами вершин, заключается в определении принадлежит ли текущий пиксель внутренней части многоугольника. Если принадлежит, то пиксель заносится.

Определить принадлежность пикселя многоугольнику можно, например, подсчетом суммарного угла с вершиной на пикселе при обходе контура многоугольника. Если пиксель внутри, то угол будет равен 360⁰, если вне – 0⁰ (рис.4.1.).

Вычисление принадлежности должно производиться для всех пикселей экрана и так как большинство пикселей скорее всего вне многоугольников, то данный способ слишком расточителен. Объем лишних вычислений в некоторых случаях можно сократить использованием прямоугольной оболочки - минимального прямоугольника, объемлющего интересующий объект, но все равно вычислений будет много. Другой метод определения принадлежности точки внутренней части многоугольника будет рассмотрен ниже при изучении отсечения отрезков по алгоритму Кируса-Бека.

4.3. Построчное заполнение

Реально используются алгоритмы построчного заполнения, основанные на том, что соседние пиксели в строке скорее всего одинаковы и меняются только там где строка пересекается с ребром многоугольника. Это называется когерентностью растровых строк (строки сканирования Y_i, Y_i+1, Y_i+2 на рис. 4.2.). При этом достаточно определить X-координаты пересечений строк сканирования с ребрами. Пары отсортированных точек пересечения задают интервалы заливки.

Кроме того, если какие-либо ребра пересекались i-й строкой, то они скорее всего будут пересекаться также и строкой i+1. (строки сканирования Y_i и Y_i+1 на рис. 4.2.). Это называется когерентностью ребер. При переходе к новой строке легко вычислить новую X-координату точки пересечения ребра, используя X-координату старой точки пересечения и тангенс угла наклона ребра:

Xi+1 = Xi + 1/k

(тангенс угла наклона ребра - k = dy/dx, так как dy = 1, то 1/k = dx).

Смена же количества интервалов заливки происходит только тогда, когда в строке сканирования появляется вершина.

Учет когерентности строк и ребер позволяет построить для заполнения многоугольников различные высокоэффективные алгоритмы построчного сканирования. Для каждой строки сканирования рассматриваются только те ребра, которые пересекают строку. Они задаются списком активных ребер (САР). При переходе к следующей строке для пересекаемых ребер перевычисляются X-координаты пересечений. При появлении в строке сканирования вершин производится перестройка САР. Ребра, которые перестали пересекаться, удаляются из САР, а все новые ребра, пересекаемые строкой заносятся в него.

Общая схема алгоритма, динамически формирующего список активных ребер и заполняющего многоугольник снизу-вверх, следующая:

1. Подготовить служебные целочисленные массивы Y-координат вершин и номеров вершин.

2. Совместно отсортировать Y-координаты по возрастанию и массив номеров вершин для того, чтобы можно было определить исходный номер вершины.

3. Определить пределы заполнения по оси Y - Y_мin и Y_max. Стартуя с текущим значением Y_tek = Y_min, исполнять пункты 4-9 до завершения раскраски.

4. Определить число вершин, расположенных на строке Y_tek - текущей строке сканирования.

5. Если вершины есть, то для каждой из вершин дополнить список активных ребер, используя информацию о соседних вершинах. Для каждого ребра в список активных ребер заносятся:

o максимальное значение Y-координаты ребра,

o приращение X-координаты при увеличении Y на 1,

o начальное значение X-координаты.

Если обнаруживаются горизонтальные ребра, то они просто закрашиваются и информация о них в список активных ребер не заносится.Если после этого обнаруживается, что список активных ребер пуст, то заполнение закончено.

6. По списку активных ребер определяется Y_след - Y-координата ближайшей вершины. (Вплоть до Y_след можно не заботиться о модификации САР а только менять X-координаты пересечений строки сканирования с активными ребрами).

7. В цикле от Y_tek до Y_след:

o выбрать из списка активных ребер и отсортировать X-координаты пересечений активных ребер со строкой сканирования;

o определить интервалы и выполнить закраску;

o перевычислить координаты пересечений для следующей строки сканирования.

8. Проверить не достигли ли максимальной Y-координаты. Если достигли, то заливка закончена, иначе выполнить пункт 9.

9. Очистить список активных ребер от ребер, закончившихся на строке Y_след и перейти к пункту 4.

4.4. Заливка области с затравкой

Как уже отмечалось, для приложений, связанных в основном с интерактивной работой, используются алгоритмы заполнения области с затравкой.

При этом тем или иным образом задается заливаемая (перекрашиваемая) область, код пикселя, которым будет выполняться заливка и начальная точка в области, начиная с которой начнется заливка.

По способу задания области делятся на два типа:

· гранично-определенные, задаваемые своей (замкнутой) границей такой, что коды пикселей границы отличны от кодов внутренней, перекрашиваемой части области. На коды пикселей внутренней части области налагаются два условия - они должны быть отличны от кода пикселей границы и кода пикселя перекраски. Если внутри гранично-определенной области имеется еще одна граница, нарисованная пикселями с тем же кодом, что и внешняя граница, то соответствующая часть области не должна перекрашиваться;

· внутренне-определенные, нарисованные одним определенным кодом пикселя. При заливке этот код заменяется на новый код закраски.

В этом состоит основное отличие заливки области с затравкой от заполнения многоугольника. В последнем случае мы сразу имеем всю информацию о предельных размерах части экрана, занятой многоугольником. Поэтому определение принадлежности пикселя многоугольнику базируется на быстро работающих алгоритмах, использующих когерентность строк и ребер (см. предыдущий раздел). В алгоритмах же заливки области с затравкой нам вначале надо прочитать пиксель, затем определить принадлежит ли он области и если принадлежит, то перекрасить.

Заливаемая область или ее граница - некоторое связное множество пикселей. По способам доступа к соседним пикселям области делятся на 4-х и 8-ми связные. В 4-х связных областях доступ к соседним пикселям осуществляется по четырем направлениям - горизонтально влево и вправо и вертикально вверх и вниз. В 8-ми связных областях к этим направлениям добавляются еще 4 диагональных. Используя связность мы может, двигаясь от точки затравки, достичь и закрасить все пиксели области.

Важно отметить, что для 4-х связной прямоугольной области граница 8-ми связна (рис. 4.3.а) и наоборот у 8-ми связной области граница 4-х связна (см. рис. 4.3.б). Поэтому заполнение 4-х связной области 8-ми связным алгоритмом может привести к "просачиванию" через границу и заливке пикселей в примыкающей области.

В общем, 4-х связную область мы можем заполнить как 4-х, так и 8-ми связным алгоритмом. Обратное же неверно. Так область на рис. 4.3.а мы можем заполнить любым алгоритмом, а область на рис. 4.3.б, состоящую из двух примыкающих 4-х связных областей можно заполнить только 8-ми связным алгоритмом.

С использованием связности областей и стека можно построить простые алгоритмы закраски как внутренней, так и гранично-определенной области

4.5. Построчный алгоритм заливки с затравкой

Использует пространственную когерентность:

· пиксели в строке меняются только на границах;

· при перемещении к следующей строке размер заливаемой строки скорее всего или неизменен или меняется на 1 пиксель.

Таким образом, на каждый закрашиваемый фрагмент строки в стеке хранятся координаты только одного начального пикселя, что приводит к существенному уменьшению размера стека.

Последовательность работы алгоритма для гранично определенной области следующая:

1. Координата затравки помещается в стек, затем до исчерпания стека выполняются пункты 2-4.

2. Координата очередной затравки извлекается из стека и выполняется максимально возможное закрашивание вправо и влево по строке с затравкой, т.е. пока не попадется граничный пиксель. Пусть это Хлев и Хправ, соответственно.

3. Анализируется строка ниже закрашиваемой в пределах от Хлев до Хправ и в ней находятся крайние правые пиксели всех не закрашенных фрагментов. Их координаты заносятся в стек.

4. То же самое проделывается для строки выше закрашиваемой.

ОТСЕЧЕНИЕ ОТРЕЗКОВ

5.1. Введение

Если изображение выходит за пределы экрана, то на части дисплеев увеличивается время построения за счет того, что изображение строится в "уме". В некоторых дисплеях выход за пределы экрана приводит к искажению картины, так как координаты просто ограничиваются при достижении ими граничных значений, а не выполняется точный расчет координат пересечения (эффект "стягивания" изображения). Некоторые, в основном, простые дисплеи просто не допускают выхода за пределы экрана. Все это, особенно

123Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: