Работа трансформатора под нагрузкой, векторная диаграмма.

Трансформаторы

Принцип работы трансформатора. Уравнение трансформаторной ЭДС.

Трансформатор предназначен для преобразования переменного тока одного напряжения в переменный ток другого напряжения.Трансформаторы делятся на повышающие (как правило, для передачи электроэнергии) и понижающие. Кроме того различают трансформаторы малой мощности (до 300 ВА) и большой мощности (более 300 ВА).

Принцип работы трансформатора

Трансформатор состоит из 2-х катушек, первичной и вторичной, расположенных на сердечнике, выполненном из тонких стальных пластин.

В том случае, если первичное напряжение u₁=U_1msin w t в первичной катушке возникает ток I₀. Пренебрегая активным сопротивлением катушки R₀ (R₀ <<w L) и потерями на гистерезис и вихревые токи, получаем:

 

Ток отстает по фазе от приложенного напряжения на угол 90⁰ из-за наличия индуктивного сопротивления w L.

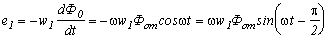Следует отметить, что наличие ферромагнитного сердечника обладающего нелинейными свойствами приводит к тому, что ток в трансформаторе оказывается несинусоидальным. Этот ток, при рассмотрении процессов, происходящих в трансформаторе, заменяют синусоидальным током, эквивалентным по действующему значению току несинусоидальному.Вследствие наличия тока возникает переменный магнитный поток Ф₀,совпадающий по фазе с током I_0. При появлении переменного магнитного потока Ф₀=Ф₀ sinwt в первичной и вторичной обмотках наводятся ЭДС e₁ и e₂:

 

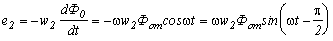
Переходя к действующим значениям с учетом того, что w=2pf получаем формулу трансформаторной ЭДС.

Е₁=4,44 fw₁Ф_om; Е₂=4,44 fw₂Ф_om (4.1)

В соответствие со вторым законом Кирхгофа u₁= -e₁=0, u₂ =e₂,

получаем 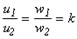-коэффициент трансформации.

Коэффициент трансформации k может быть определен в режиме холостого хода.

 

Схема замещения трансформатора.

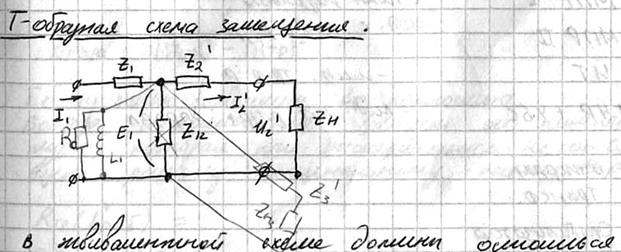
В эквивалентной схеме должны остаться неизменными структура вторичной цепи и полная активная и реактивная мощности, которые выделяются в каждом элементе трансформатора

Е₁=Е₂’

(E₁/E₂)=(W₁/W₂₎=k₁₂

Пересчет токов: U₂I₂=U’₂I’₂ I’₂=I₂k₂₁=I₂/k₁₂

I₂²R_H= (I’₂)²R_H’=> R_H’=R_H(k12)²

В ряде случаев схему замещения можно упростить

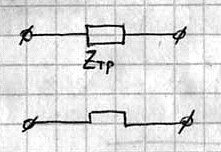
I_xx<<I_HOM

R_TP=R₁+R’₂

X_PTP=X_P1+X’_P2

Работа трансформатора под нагрузкой, векторная диаграмма.

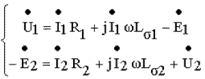При подключении сопротивления нагрузки Z_н к зажимам вторичной обмотки в ней появляется ток i₂ и уравнения электрического состояния трансформатора можно записать в виде:

Эти уравнения, записанные в комплексной форме относительно эквивалентных синусоид, ничем не отличаются от соответствующих уравнений воздушного трансформатора.

Анализируя работу трансформатора под нагрузкой, важно уяснить взаимосвязь тока в цепи нагрузки i₂ с током, потребляемым трансформатором от сети, поскольку изменение мощности, отдаваемой трансформатором в нагрузку должно сопровождаться изменением мощности, потребляемой трансформатором от сети. Эта взаимосвязь устанавливается через уравнение магнитного состояния трансформатора. При изучении воздушного трансформатора нами было установлено, что Ф=Ф₁-Ф₂, т.е. основной или рабочий поток трансформатора равен алгебраической сумме потоков взаимоиндукции первичной и вторичной обмоток Ф₁ и Ф₂ или

где λ_М - магнитная проводимость участка, по которому замыкаются потоки взаимоиндукции. (В соответствие с принципом Ленца поток Ф₁ направлен встречно потоку Ф₂.),следовательно под нагрузкой:

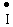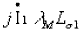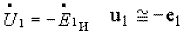Если пренебречь напряжениями ₁R₁ и по сравнению с ЭДС , т.е. считать, что , то поток в сердечнике будет однозначно определяться приложенным напряжением, как было показано выше. Следовательно, поток в сердечнике при одинаковом напряжении будет одинаковым как в режиме ХХ, так и под нагрузкой, т.е.

Ф_к=Ф или Ф_к= Ф₁- Ф₂.

Физически взаимосвязь токов i₁ и i₂ объясняется следующим образом: в режиме ХХ ток холостого хода i_1x создает поток в сердечнике Ф_1x, обуславливающий ЭДС

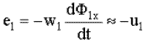Ток i₂, протекающий через нагрузку, создает поток Ф₂, стремящийся ослабить поток Ф. Но уменьшение потока Ф приводит к уменьшению ЭДС e₁, и, следовательно, к нарушению равенства u₁≈-e₁. Следовательно, ток i₁ начинает возрастать и будет расти до тех пор, пока поток не достигнет прежнего значения Ф_1x. Из равенства Ф_1x= Ф₁- Ф₂ или _1x= ₁- ₂, поскольку потоки синусоидальны, следует, что

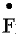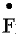_1x= ₁- 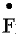₂ Последнее уравнение представляет собой закон равновесия намагничивающих сил трансформатора или уравнения магнитного состояния трансформатора. Поскольку 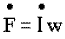, последнее уравнение можно записать в виде

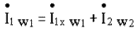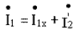или ,где 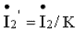- приведенный ток вторичной обмотки. Согласно последнему уравнению ток, потребляемый трансформатором от сети 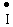₁, имеет 2 составляющие: составляющая 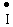_1x создает рабочий поток в сердечнике и компенсирует потери в стали, составляющая 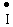₂′ (нагрузочная составляющая) компенсирует размагничивающее действие на сердечник тока вторичной обмотки и обеспечивает поступление в трансформатор от сети мощности, отдаваемой в нагрузку.

Векторная диаграмма трансформатора, работающего на нагрузку, приведена на рис. 2.4.

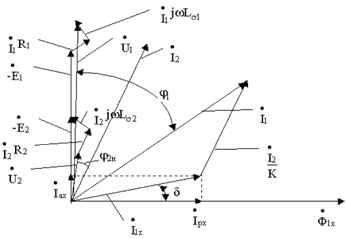
Рис. 2.4

 

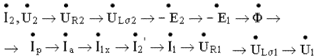
Порядок построения диаграммы:

 

Поделиться:

Воспользуйтесь поиском по сайту: