Напряжённость электрического поля

Физическая величина, равная отношению силы, с которой электрическое поле действует на точечный электрический заряд, к значению этого заряда, называется напряженностью электрического поля. Обозначив напряженность буквой , запишем

Зако́н Куло́на — это закон, описывающий силы взаимодействия между неподвижными точечными электрическими зарядами. В векторном виде в формулировке Ш. Кулона закон записывается следующим образом:

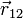где — сила, с которой заряд 1 действует на заряд 2; — величина зарядов; — радиус-вектор (вектор, направленный от заряда 1 к заряду 2, и равный, по модулю, расстоянию между зарядами — ); 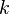— коэффициент пропорциональности

Напряжённость электри́ческого по́ля — векторная физическая величина, характеризующая электрическое поле в данной точке и численно равная отношению силы действующей на неподвижный^[1] пробный заряд, помещенный в данную точку поля, к величине этого заряда :

.

Из этого определения видно, почему напряженность электрического поля иногда называется силовой характеристикой электрического поля (действительно, всё отличие от вектора силы, действующей на заряженную частицу, только в постоянном^[2] множителе).

В каждой точке пространства в данный момент времени существует свое значение вектора 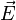(вообще говоря - разное^[3] в разных точках пространства), таким образом, 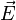- это векторное поле. Формально это выражается в записи

Если в электрическое поле, создаваемое зарядом Q, поместить еще один заряд Q0, то оно будет воздействовать на него с определенной силой. Это характеристика называется напряженностью электрического поля E. Она представляет собой отношение силы F, с которое поле действует на положительный электрический заряд Q0 в определенной точке пространства, к значению этого заряда: E = F/Q0.

В зависимости от конкретной точки пространства, значение напряженности поля E может меняться, что выражается формулой Е = Е (x, y, z, t). Поэтому напряженность электрического поля относится к векторным физическим величинам.

Поскольку напряженность поля зависит от силой, действующей на точечный заряд, то вектор напряженности электрического поля E одинаков с вектором силы F. Согласно закону Кулона, сила, с которой взаимодействуют две заряженные частицы в вакууме, направлена по прямой линии, которая соединяет эти заряды.

Майкл Фарадей предложил наглядно изображать напряженность поля электрического заряда с помощью линий напряженности. Эти линии совпадают с вектором напряженности во всех точках по касательной. На чертежах их принято обозначать стрелками.

В том случае, если электрическое поле однородно и вектор его напряженности постоянен по своему модулю и направлению, то линии напряженности параллельны с ним. Если электрическое поле создается положительно заряженным телом, линии напряженности направлены от него, а в случае с отрицательно заряженной частицей - по направлению к нему.

339-349 Электростатический потенциа́л (см. также кулоновский потенциал) — скалярная энергетическая характеристика электростатического поля, характеризующая потенциальную энергию поля, которой обладает единичный положительный пробный заряд, помещённый в данную точку поля. Единицей измерения потенциала в Международной системе единиц (СИ) является вольт (русское обозначение: В; международное: V), 1 В = 1 Дж/Кл (подробнее о единицах измерения — см. ниже).

Электростатический потенциал — специальный термин для возможной замены общего термина электродинамики скалярный потенциал в частном случае электростатики (исторически электростатический потенциал появился первым, а скалярный потенциал электродинамики — его обобщение). Употребление термина электростатический потенциал определяет собой наличие именно электростатического контекста. Если такой контекст уже очевиден, часто говорят просто о потенциале без уточняющих прилагательных.

Электростатический потенциал равен отношению потенциальной энергии взаимодействия заряда с полем к величине этого заряда:

Напряжённость электростатического поля и потенциал 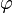связаны соотношением^[1]

или обратно^[2]:

Здесь — оператор набла, то есть в правой части равенства стоит минус градиент потенциала — вектор с компонентами, равными частным производным от потенциала по соответствующим (прямоугольным) декартовым координатам, взятый с противоположным знаком.

Воспользовавшись этим соотношением и теоремой Гаусса для напряжённости поля , легко увидеть, что электростатический потенциал удовлетворяет уравнению Пуассона. В единицах системы СИ: