 |
Спин ядра и моменты нуклонов
|
|
|
|
Основные характеристики атомных ядер
Перечислим основные характеристики ядер, которые будут обсуждаться далее:
1. Размеры ядер.
2. Энергия связи нуклонов в ядре и энергии отделения нуклонов и кластеров от ядра.
3. Спин, четность и изоспин ядер в основных и возбужденных состояниях.
4. Спектры ядер.
5. Электромагнитные моменты ядра и нуклонов
Размеры ядер
Распределение заряда и массы в атомных ядрах исследуется в экспериментах по упругому рассеянию на ядрах альфа-частиц (исторически это первые эксперименты Резерфорда), электронов и протонов. Выяснилось, что как плотность распределения заряда, так и плотность распределения массы ядра приближенно выражаются распределением Ферми:
 
| (1.5) |
Величину R называют радиусом ядра. Отметим, что поскольку распределение плотности заряда и массы близки, но не совпадают друг с другом, отличаются также и зарядовый и массовый радиусы. В приближенных расчетах можно считать эти величины совпадающими и полагать, что радиус ядра
R 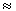 r0A1/3. r0A1/3.
| |||||||||||||
Основные характеристики атомных ядер За более чем 70 лет исследования атомных ядер физикой ядра накоплен громадный объем экспериментальных данных. Интерпретация этих данных является задачей теории ядра. Перечислим основные характеристики ядер, которые будут обсуждаться далее:
Размеры ядер Распределение заряда и массы в атомных ядрах исследуется в экспериментах по упругому рассеянию на ядрах альфа-частиц (исторически это первые эксперименты Резерфорда), электронов и протонов. Выяснилось, что как плотность распределения заряда, так и плотность распределения массы ядра приближенно выражаются распределением Ферми:
Величину R называют радиусом ядра. Отметим, что поскольку распределение плотности заряда и массы близки, но не совпадают друг с другом, отличаются также и зарядовый и массовый радиусы. В приближенных расчетах можно считать эти величины совпадающими и полагать, что радиус ядра
Это одновременно означает независимость средней плотности ядра от массового числа. Действительно, оценим плотность ядра с числом нуклонов А:
Полученные результаты для плотности и радиуса эквивалентны утверждению о полной несжимаемости ядерной материи. В большинстве приближенных расчетов это утверждение можно использовать, однако отклонение от него хорошо видно на примере распределениясреднеквадратичного радиуса распределения заряда для разных ядер. На рис.1.1 показаны результаты исследований среднеквадратичного зарядового радиуса для некоторых ядер, полученные в экспериментах по неупругому рассеянию электронов на ядрах. Следует обратить внимание на отклонение величины зарядового радиуса от (1.6). Например, зарядовый радиус ядра 48Са меньше, чем зарядовый радиус ядра 40Са. Для изотопов титана рост А ведет к уменьшению зарядового радиуса. Эти эффекты нашли качественное объяснение в модели ядерных оболочек. Энергии связи и массы ядер Масса стабильных ядер меньше суммы масс входящих в ядро нуклонов, - разность этих величин и определяет энергию связи ядра Eсв (binding energy):
В (1.9) MN - масса ядра. В таблицах масс приводятся не массы ядер, а массы нейтральных атомов, либо величины, с ними связанные. В приложении к сборнику “Субатомная физика” приведены значения “избытков масс”
| |||||||||||||
Спин ядра и моменты нуклонов
Основное и возбужденные состояния ядра и других квантовых систем характеризуется набором квантовых чисел, являющихся собственными значениями операторов физических величин. Квантовый оператор F называется собственным оператором, если его действие на волновую функцию системы приводит к той же волновой функции, умноженной на число - собственное значение оператора:

 = f
= f  .
.
Примерами таких операторов являются оператор квадрата момента количества движения квантовой системы и оператор проекции момента количества движения на выделенную ось. Собственные значения операторов физических величин сохраняются или, как иногда говорят, являются хорошими квантовыми числами, если соответствующий оператор коммутирует с полным гамильтонианом квантовой системы.
|
|
|



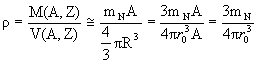 .
.
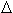 = M - A, где М – масса нейтрального атома в МэВ. (Избытки масс и не только можно найти в базе данных "Параметры основных состояний атомных ядер"). Величина А представляет собой в данном случае произведение числа нуклонов на значение единицы массы в МэВ. Таким образом, величины
= M - A, где М – масса нейтрального атома в МэВ. (Избытки масс и не только можно найти в базе данных "Параметры основных состояний атомных ядер"). Величина А представляет собой в данном случае произведение числа нуклонов на значение единицы массы в МэВ. Таким образом, величины