Лекция 5 Расчеты на долговечность в САЕ системе

I. МНОГОЦИКЛОВОЕ УСТАЛОСТНОЕ РАЗРУШЕНИЕ

1. ЯВЛЕНИЕ УСТАЛОСТНОГО РАЗРУШЕНИЯ МЕТАЛЛОВ

Ответственные детали большинства машин при эксплуатации подвергаются действию циклически изменяющихся во времени напряжений, что создает условия для возникновения особого вида разрушения, называемого усталостью. Способность сопротивляться действию переменных напряжений называют выносливостью материала.

 

 

Механизм возникновения перемен­ных во времени напряжений обсудим на известном примере нагружения оси железнодорожного вагона. Вначале рас­смотрим случай, когда вагон неподви­жен. На рис. 1 показаны обусловленные действием силы тяжести P эпюры изгибающего момента и нормальных напряжений в сечениях среднего участка оси. При движении вагона по ровному участку пути, когда колебания его корпуса тсутствуют и внешние силы остаются неизменными, вращение осей приводит к изменению положения точек на поверхности сечений по отношению к плоскости действия постоянного изгиба­ющего момента M = Pa/2 (на рис. 1 цифрами 1... 8 показаны различные положения одной из точек на поверх­ности сечения).

Таким образом, за время одного оборота колеса в каждой точке поверхности оси железнодорожного вагона напряжения изменяются во времени по гармоническому закону o(t), проходя нулевые значения (положения точки 1 и 5) и достигая максимальных значений растягивающих и сжимающих напряжений (положения точки 3 и 7 соответственно). Частота изменения напряжений определяется скоростью движения поезда.

Легко убедиться в том, что во время одного рейса поезда дальнего следования Москва- Владивосток-Москва описанный цикл изменения напряжений в осях вагонов повторяется более пяти миллионов раз.

В соответствии с государственным стандартом (ГОСТ 23207-78 "Сопротивление усталости. Основные термины, определения и обозначения") усталостью называют процесс постепенного накопления повреждений материала под действием переменных напряжений, приводящих к изменению его свойств, образованию и развитию трещин и разрушению.

Различают две основные разновидности усталостного повреждения:

I. малоцикловая усталость возникает при максимальных напряжениях, превышающих предел текучести материала, и сопровождается знакопеременным пластическим деформированием объема материала, большого по сравнению с размерами структурных составляющих (зерен, пор, включений). Число циклов до образования заметной трещины (длиной 0,5 - 1 мм и более) зависит в основном от величины пластической деформации детали в каждом цикле и от способности материала сопротивляться малоцикловому разрушению; для стальных конструкций оно не превышает 10⁴. Явление малоцикловой усталости знакомо каждому, кто ломал проволоку, пластически деформируя ее в разные стороны.

II. многоцикловая усталость имеет место при напряжениях значительно ниже предела текучести (<c_max < 0,6с_Т). В этом случае в макрообъеме материал деформируется упруго (его свойства с вполне удовлетворительной точностью описываются законом Гука ст = Es). Однако большинство реальных материалов имеют сложную многокомпонентную структуру (зерна, поры, межзеренные прослойки, неметаллические включения в стали и т. д.). При упругом деформировании достаточно большого объема в микрообъемах (в отдельных слабых зернах, вблизи дефектов) происходит локальное знакопеременное пластическое деформирование, которое называют микропластическим. Его многократное повторение приводит к зарождению микроскопических трещин. Постепенное их развитие и слияние в магистральную трещину приводит к ослаблению сечений и затем к внезапному долому деталей. Продолжительность стадии многоцикловой усталости к моменту зарождения магистральной усталостной макротрещины для стальных конструкций превышает 10⁵ - 10⁶ циклов.

Граница между малоцикловой и многоцикловой усталостью не является четко выраженной. В тех случаях, когда пластическая деформация в макрообъеме отлична от нуля в каждом цикле, но мала по сравнению с упругой, условия зарождения трещины зависят и от упругой и от пластической деформации. Это - переходная зона между малоцикловой и многоцикловой усталостью.

Рассмотрим вначале случай многоцикловой усталости металлов. В качестве предельного состояния детали здесь принимается образование магистральной трещины длиной 0,1...0,5 мм, т.е. анализ ограничивается начальной стадией усталостного разрушения. В последующем в тексте пособия образование такой трещины будет условно называться усталостным разрушением.

 

Расчет в системе NASTRAN

Работа по расчету зубчатого венца привода шаровой мельницы проводилась в следующем объёме и последовательности:

1. Составление расчетной схемы, соответствующей схеме испытательного нагружения. Назначение режимов нагружения.

2. Назначение характеристик сопротивления усталости конструкционных материалов.

В отсутствии экспериментальных данных использовалось два способа получения исходных данных с помощью встроенного в программу MSC/Fatigue генератора по материалам:

- характеристик сопротивления усталости материала по его типу и основным характеристикам – модулю упругости и временному сопротивлению разрыву.

3. Построение с помощью программы MSC / Patran конечно-элементной модели (далее - КЭМ) рассчитываемой конструкции, граничных условий, соответствующих закреплению зубчатого колеса в экспериментальной оснастке, а также модели внешней нагрузки.

4. Проведение расчета напряженно - деформированного состояния (далее – НДС) КЭМ в объеме, необходимом для выполнения оценки долговечности этой конструкции с помощью программы MSC / Fatigue. Использовались программы MSC / Patran, MSC / Nastran.

5. Расчет долговечности зубчатого венца с помощью модуля MSC / Fatigue, обзор возможностей этого модуля.

Учитывая особенности рассчитываемой конструкции, в качестве расчетной принята схема нагружения, изображенная на рисунке 3.4.

 

 

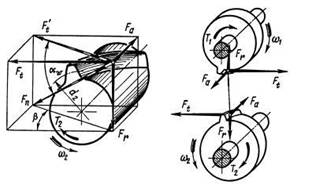
Рисунок 3.4 – Схема нагружения

 

Данные по силам, действующих в зацеплении зубчатого венца и вала-шестерни были расчитаны в приложении А.

- окружное усилие: F_t = 5362315 H;

- радиальное усилие в зубчатом зацеплении: F_t = 195972 H;

- осевое усилие: F_а = 49333 H.

Практические способы получения характеристик сопротивления усталости материала или детали, необходимые для расчета долговечности (перечислены по мере убывания достоверности рассчитанной на их основе долговечности) состоят в следующем:

1. Построение экспериментальной кривой сопротивления усталости детали. Для этого необходимо партию (20-30 шт.) одинаковых зубчатых колес испытать на изгиб с вращением на разных уровнях нагрузки и построить зависимость числа циклов до разрушения от уровня нагрузки. Этот метод дает наибольшую достоверность оценки долговечности, но требует больших затрат времени и средств.

2. Использование кривых усталости материалов, реализуемых в конструкции зубчатого венца, полученных в соответствии с ГОСТ 25.507-85 «Методы испытания на усталость».

3. Использование статистики по уже проведенным на условия ГОСТ 37.001.404-97 испытаниям зубчатых венцов. Для колес с известными числами циклов до разрушения при заданной нагрузке строится расчетная модель для определения НДС, реализованного при испытаниях. Расчетом определяется уровень напряжений, приведший к разрушению венца за известное (по протоколу испытаний) число циклов нагружения. Полученный результат распространяется на вновь разрабатываемые изделия-аналоги, выполненные из данного материала по аналогичной технологии.

4. Расчет необходимых характеристик сопротивления усталости материала по известным для этого материала характеристикам статической прочности. Рекомендуется использовать ГОСТ 25.504-82 «Методы расчета характеристик сопротивления усталости».

Программа MSC / Fatigue позволяет получить необходимые для расчета долговечности исходные данные по характеристикам материалов с помощью встроенного генератора усталостных характеристик материала. При этом используется накопленный опыт разработчиков программы по характеристикам зарубежных конструкционных материалов.

Особенности способа:

1. Для задания необходимых характеристик материала требуется знать лишь его тип (выбирается по таблице «Table 3-1 Material Type Numbers and Descriptions» раздела «PFMAT Material Listing» руководства «MSC / Fatigue 2005. User’s Guide Volume I») и самые распространенные характеристики: модуль упругости E и временное сопротивление разрыву σ_в.

2. На выходе, используя эмпирические зависимости статических и усталостных свойств зарубежных материалов, получаем характеристики материала для всех видов расчета долговечности, поддерживаемых программой MSC / Fatigue.

В задаче использовались характеристики сопротивления усталости, полученные с помощью встроенного в MSC / Fatigue генератора усталостных характеристик материала, а также характеристики, рассчитанные по ГОСТ 25.504-82.

Из КД на зубчатый венец имеем следующие данные по материалам этого колеса:

- колесо изготовлено литьем, материал колеса – сталь 35ХМЛ, ГОСТ 977-88;

- временное сопротивление разрыву σ_в = 600 МПа;

- модуль упругости первого рода Е = 2,1∙10⁵ МПа.

По таблице 3-1 руководства «MSC Fatigue 2005 User’s Guide Volume I» выбираем наиболее близкий к стали 35ХМЛ тип материала:

«№13 - Plain carbon wrought steel with < 0,2 % carbon (PCWS)». Как ГОСТ 25.504-82, так и программа MSC / Fatigue используют кривую усталости степенного вида, но записывают ее в разных терминах.

В соответствии с ГОСТ 25.504-82 характеристики сопротивление усталости материала описываются кривой усталости, представляющей зависимость числа циклов N до разрушения стандартного образца от уровня амплитудыциклов напряжений S в расчетном сечении этого образца [79].

Вид кривой усталости:

 

, (3.24)

 

где σ_-1 – ограниченный предел выносливости материала конструкции на базе N_b циклов нагружения;

m – показатель наклона кривой усталости, аппроксимированной степенным уравнением.

В логарифмических координатах кривая усталости имеет два прямых участка с разным углом наклона относительно оси X (рисунок 3.5):

- при N < N_b показатель наклона m для гладких стандартных образцов в отсутствие экспериментальных данных необходимо рассчитывать по формуле:

 

(3.25)

 

- при N => N_b кривая усталости параллельна оси X.

В отсутствии экспериментальных данных предел ограниченной выносливости для сталей данного типа допускается определять на базе N_б = 10⁷ циклов по формуле:

 

(3.26)

 

 

 

 

Рисунок 3.5 - Схематизация кривой усталости материала

 

В программу MSC/Fatigue заложено описание характеристик cопротивления усталости материала в виде кривой усталости, представляющей собой зависимость числа циклов до разрушения стандартного образца N от уровня размахов циклов напряжений в расчетном сечении этого образца S1.

Вид кривой усталости:

 

, (3.27)

 

где – отрезок, отсекаемый на оси размахов в точке 0 циклов;

– показатели наклонов двух участков кривой усталости.

Вероятность достижения предельного состояния задается с помощью СКО логарифма числа циклов до разрушения, которое определяет степень рассеяния характеристик усталости. Для получения достоверных результатов расчета долговечности данная характеристика должна быть получена обобщением экспериментальных данных по характеристикам материалов, реализующихся на конкретном производстве, с учетом разброса свойств внутри одной партии заготовок и между разными партиями.

Программа Log S, Log Nб, Log N MSC/Fatigue позволяет получить обобщенную характеристику рассеяния в зависимости от типа материала, модуля упругости и временного сопротивления разрыву. Характеристика стали 35ХМЛ представлен в таблице 3.2.

 

Таблица 3.2 – Характеристика стали 35ХМЛ в терминах ГОСТ 25.504-82

 

Материал	σв, МПа	Е, МПа	σ-1, МПа	M	Nb
Сталь 35ХМЛ		2.1*105		9,6	107

 

Изображения кривых усталости стали Сталь 35ХМЛ, полученные с помощью операции «Graphic display» из основного окна модуля MSC / Fatigue, приведены на рисунке 3.6.

 

 

Рисунок 3.6 – Кривая усталости материала сталь

 

Создание конечно-элементной модели (КЭМ) зубчатого венца, модели внешней нагрузки и граничных условий, имитирующих закрепление этого колеса к барабану, выполнялось следующая последовательность.

Создание 3D (рисунок 3.7) модели осуществлялось в cad программе КОМПАС модуле Shaft по геометрические параметрам расчитанным в работе.

При создания расчетной модели был вырезан фрагмент колеса, для того чтобы не расходовать ресурсы машины, так как напряжения будут локализованы по площади зуба венца.

 

 

Рисунок 3.7 – 3D модель сборки колеса и шестерни

 

Модель, созданная в российской САПР была успешно импортирована посредством обмена файлов в CAE систему NASTRAN. Разбиение на конечные элементы смоделированы объемными элементами типа tet. Расчетная схема для определения действующих напряжений приведена на рисунке 3.8. Требования к типу элементов и качеству сетки должны быть повышенные, так как для оценки усталостной прочности требуется расчет локальных напряжений с учетом их концентрации.

Как следует из предыдущего раздела, показатель наклона кривой усталости стали 35ХМЛ составляет 7,5…9,6. Уравнение кривой усталости имеет вид:

 

(3.28)

 

Механическая расчетная схема включала жесткое закрепление, предполагающая наложения связи по шести степеням свободы и нагружение в виде результирующей распределенной нагрузки по грани зуба. Модуль нагрузки по осям был подсчитан по следующей формуле:

 

, (3.29)

 

,

 

.

 

 

Рисунок 3.8 – Сгенерированная сетка

 

 

Таким образом, для определения с помощью программы MSC / Nastran НДС зубчатого венца решалась статическая задача (рисунок 3.9). Результаты расчета напряжений сохранены в одном файле с расширением *. xdb.

После того, как программа MSC/Nastran успешно закончит решение задачи «coleso.bdf», для оценок долговечности будут доступны результаты расчета НДС для каждого шага приложения нагрузки, сохраненные в одном файле «coleso.xdb». В данном разделе приведены распределения эквивалентных напряжений, вычисленные по формуле Мизеса. Результаты обобщены. Шкала напряжений на рисунках соответствует размерности [Па].

 

 

Рисунок 3.9 – Распределение эквивалентных напряжений в венце

 

Результаты напряжений показывают достаточный запас статической прочности. По диаграмме результатов максимальное напряжение имеет значение = 330 МПа, допускаемое напряжение = 600 МПа, коэффициент статической прочности определяется по формуле:

 

(3.30)

 

Но положительные результаты статического расчета не прогнозируют в полной мере долговечность конструкций или деталей машин. Как показывает практика, нагрузки, циклически изменяющиеся во времени по величине или по величине и по знаку, могут привести к разрушению конструкции при напряжениях, существенно меньших, чем предел текучести (или предел прочности). Такое разрушение принято называть «усталостным». Материал как бы «устает» под действием многократных периодических нагрузок.

Для расчет усталостной прочности и прогнозирование долговечности колеса с помощью модуля MSC / Fatigue нами разработана методика расчета представленные ниже.

В соответствии с государственным стандартом (ГОСТ 23207-78 «Сопротивление усталости. Основные термины, определения и обозначения») усталостью называют процесс постепенного накопления повреждений материала под действием переменных напряжений, приводящих к изменению его свойств, образованию и развитию трещин и разрушению.

Различают две основные разновидности усталостного повреждения:

1. Малоцикловая усталость возникает при максимальных напряжениях, превышающих предел текучести материала, и сопровождается знакопеременным пластическим деформированием объема материала, большого по сравнению с размерами структурных составляющих (зерен, пор, включений). Число циклов до образования заметной трещины (длиной 0,5-1 мм и более) зависит в основном от величины пластической деформации детали в каждом цикле и от способности материала сопротивляться малоцикловому разрушению; для стальных конструкций оно не превышает 10⁴. Явление малоцикловой усталости знакомо каждому, кто ломал проволоку, пластически деформируя ее в разные стороны.

2. Многоцикловая усталость имеет место при напряжениях значительно ниже предела текучести (σ_max < 0,6σ_Т). В этом случае в макрообъеме материал деформируется упруго (его свойства с вполне удовлетворительной точностью описываются законом Гука σ = E_ε). Однако большинство реальных материалов имеют сложную многокомпонентную структуру (зерна, поры, межзеренные прослойки, неметаллические включения в стали и т. д.). При упругом деформировании достаточно большого объема в микрообъемах (в отдельных слабых зернах, вблизи дефектов) происходит локальное знакопеременное пластическое деформирование, которое называют микропластическим. Его многократное повторение приводит к зарождению микроскопических трещин. Постепенное их развитие и слияние в магистральную трещину приводит к ослаблению сечений и затем к внезапному долому деталей. Продолжительность стадии многоцикловой усталости к моменту зарождения магистральной усталостной макротрещины для стальных конструкций превышает 10⁵-10⁶ циклов.

Граница между малоцикловой и многоцикловой усталостью не является четко выраженной. В тех случаях, когда пластическая деформация в макрообъеме отлична от нуля в каждом цикле, но мала по сравнению с упругой, условия зарождения трещины зависят и от упругой и от пластической деформации. Это – переходная зона между малоцикловой и многоцикловой усталостью [79].

Очевидно, чем выше значение амплитуды напряжений (σ_a) при фиксированных средних напряжениях σ_m, тем ниже число циклов (N), которое образец "может выдержать" до момента зарождения магистральной усталостной трещины. Таким образом, в отличие от статических испытаний, где определяются отдельные значения различных параметров (σ_т, σ_0,2, σ_в, ψ, δ, и др.), при усталостных испытаниях характеристикой выносливости конкретного материала становится зависимость . Для определения этой зависимости необходимо испытать партию (минимум 10…15 штук) одинаковых образцов из исследуемой марки стали, т.е. образцов из одной партии (плавки), с одинаковыми размерами, термообработкой, качеством поверхности. Ограничимся пока рассмотрением симметричного цикла (σ_m= 0, R = –1) при линейном напряженном состоянии. Первый образец испытывают при наибольшей амплитуде напряжений, составляющей (0,6…0,75) σ_в, а последующие при снижающихся амплитудах. Каждому разрушившемуся образцу соответствует одна точка на графике; обработка результатов испытаний всех образцов методом наименьших квадратов позволяет получить зависимость среднего числа циклов до разрушения от амплитуды переменных напряжений. Ее называют кривой выносливости или кривой Велера по имени немецкого ученого, впервые начавшего в конце XIX века системные исследования усталостного разрушения.

Кривая выносливости могут быть построены при различных значениях коэффициента асимметрии цикла R₁. На рисунке 3.10 показан типичный вид таких кривых для малоуглеродистой (кривая 1, экспериментальные данные отмечены точками) и легированной 9 (кривая 2, экспериментальные данные отмечены крестиками) сталей. В логарифмических координатах кривые выносливости хорошо схематизируют кусочно-линейными зависимостями. Такая схематизация позволяет описать результаты испытаний минимальным набором параметров. Кривые первого типа (рисунок 3.10, а) характерны для сталей малой и средней прочности (σ_в < 1200 МПа) при нормальной температуре; кривые, изображенные на рисунке 3.10, б – для легированных сталей и титановых сплавов; кривые третьего типа (рисунок 3.10, в) – для алюминиевых сплавов и ряда жаропрочных сплавов при повышенных температурах.

 

 

 

Рисунок 3.10 – Типичный вид для углеродистых и легированных сталей

 

На рисунке 3.11 кривые выносливости изображены для симметричного цикла; их характеристики обычно считаются основными. Точка перелома на кривых первого типа обычно соответствует 10⁶ – 10⁷ циклам, отвечающая ей амплитуда напряжений обозначается σ_-1 и называется физическим пределом выносливости. При меньших амплитудах (σ_а < σ₁) усталостное разрушение не наблюдается при числах циклов до 10¹² (при больших числах циклов испытания обычно не проводятся).

 

 

а) б) в)

 

Рисунок 3.11 – Кривые выносливости для симметрического цикла

 

Для кривых выносливости второго и третьего типа находится условный предел выносливости σ-_1N – значение амплитуды напряжений, при котором происходит разрушение при заданном базовом числе циклов N, обычно N = 2⋅10⁶…5⋅10⁷ циклов. Для кривых второго типа определяется также число циклов, соответствующее точке перелома N_G (если оно не совпадает с σ-_1N) и соответствующая амплитуда напряжений. Кроме того, определяется наклон кривой выносливости. В частности, для первого участка кривых, изображенных на рисунке 3.11, а и 3.11, в.

Наклон кривой выносливости определяется по формуле:

 

(3.31)

 

Уравнение кривой выносливости первого типа удобно записать теперь в виде:

 

, при (3.32)

при

 

Уравнение кривой второго типа

 

при , (3.33)

 

при (3.34)

 

Результаты испытаний образцов одной и той же стали при растяжении-сжатии и изгибе качественно одинаковы, но значения характеристик (в частности – предела выносливости) могут заметно различаться. В справочниках по свойствам материалов приводят значения пределов выносливости для каждого их этих видов нагружения. Аналогичные характеристики выносливости материалов при чистом сдвиге получают путем испытаний образцов на кручение; при их обозначают соответственно τ_a, τ_m, τ_–1, τ_R и т.д.

В случаях, когда в справочной литературе отсутствуют характеристики усталости интересующей марки стали, рекомендуется определять их по приближенным корреляционным зависимостям:

 

,

,(3.35)

 

где σ_вр – временное сопротивление при растяжении, МПа;

K_{σ Д (τ Д)} – коэффициент, учитывающий влияние различных факторов.

Сведения о характеристиках выносливости применяемых в машиностроении конструкционных сталей и сплавов приводятся в справочной литературе. В качестве примера в таблице 3.3 приведены пределы выносливости материалов.

 

Таблица 3.3 – Пределы выносливости материалов

 

Материал	тр, МПа	вр, МПа	1, МПа	-1, МПа
Сталь малоуглеродистая
Сталь 45 незакаленная
Сталь 30ХГСА закаленная, отпуск
Чугун серый	-
Алюминиевый сплав АМЦ термо-обработанный				-

 

Информация о материале с учетом конструктивных, технологических и эксплуатационных факторов влияния задается в разделе Material Info. После запуска на решение в разделе «Job Control» главного окна модуля переключаемся в акцию «Monitor Job». Жмем «Apply» и видим информацию по ходу выполнения работы. Через некоторое время нажимаем еще раз, информация обновится (обновление информации не автоматизировано и требует запроса от пользователя в виде нажатия «Apply») (рисунок 3.13).

 

Важные файлы, создаваемые программой в рабочей директории при решении задачи (в нашем примере имя задачи «nov_test»):

1. nov_test.fin – текстовый файл с параметрами нашей работы для транслятора. Его можно просмотреть, проверить, исправить и запустить вновь на расчет.

2. nov_test.fes – бинарный файл исходных данных для решателя, с уже считанными напряжениями. Посмотреть его можно, но сначала нужно преобразовать в текстовый формат с помощью утилиты (об этом ниже).

3. nov_test.fef – файл результатов расчета долговечности, который создается решателем FEROT после запроса на выполнение Full Analysis. Это текстовый файл, который может быть прочитан программой MSC / Patran для отрисовки изолиний долговечности. На рисунке 3.14 отображен логарифм долговечности.

 

 

Рисунок 3.14 − Логарифм долговечности

 

Минимальный логарифм долговечности по диаграмме результатов 10^5.65 минимальное количество 449000 оборотов венца показан на рисунке 3.15.

 

 

Рисунок 3.15 − Диаграмма количества оборотов

По выполненному расчету можно сделать следующие выводы:

- проведен расчет напряженного состояния венца шаровой мельницы колеса с шестерней по программе NASTRAN;

- данные по напряженному состоянию получены в форме и объеме, достаточном для проведения расчета долговечности средствами модуля MSC / Fatigue.

- уровень действующих в конструкции напряжений составляет 330 МПа, что соответствует условию прочности;

- спрогнозирована долговечность, составляющая 10^5.65 циклов с учетом сложной геометрии венца и свойств материала, что не всегда возможно при вычислении долговечности по эмпирическим формулам. Это говорит о том, что после заверщения этих циклов работы зубчатой передачи, необходимо произвести ее осмотр и принять соответствующие меры, в случае обнаружения дефектов.

 

 

Поделиться:

Воспользуйтесь поиском по сайту: