 |
Элементы статистической обработки данных
|
|
|
|
РОССИЙСКАЯ АКАДЕМИЯ ПРАВОСУДИЯ
Кафедра
информационного права,
информатики и математики
ИНФОРМАЦИОННЫЕ ТЕХНОЛОГИИ
В ЮРИДИЧЕСКОЙ ДЕЯТЕЛЬНОСТИ
б) Методы и средства информационных технологий
для статистического анализа информации
УЧЕБНО-МЕТОДИЧЕСКИЕ МАТЕРИАЛЫ
К ЭКЗАМЕНУ ПО ДИСЦИПЛИНЕ
ДЛЯ СТУДЕНТОВ БАКАЛАВРИАТА
Москва
2012
Разработано проф. Королевым В.Т., доц. Радионовым В.В.
ОСНОВНЫЕ ЗАКОНОМЕРНОСТИ
СОЗДАНИЯ И ФУНКЦИОНИРОВАНИЯ
ИНФОРМАЦИОННЫХ ПРОЦЕССОВ
22. Основные закономерности создания и функционирования информационных процессов. Содержание понятия информационные технологии и структура основных информационных процессов.
Информационные технологии представляют собой организованное научно-методическое обеспечение переработки информации.
Переработка информации – это совокупность таких информационных процессов:
производство информации:генерация, включая моделирование; рецепция, измерение,
интерпретация информации: преобразование, логическая обработка, аккумуляция,
коммуникация информации: передача, хранение, представление.
Информация, как видим, является предметом и продуктом информационных технологий.
23. Толкование термина информация в философии, в кибернетике, в сфере юриспруденции.
Само базовое понятие «информация» (от лат. informatio – сведения) многозначно, а закономерности получения и преобразования информации ещё мало изучены. Отсутствует универсальный формально-логический аппарат для их описания. Поэтому смысл понятия «информация» формулируют для каждой предметной области через другие известные здесь понятия. Можно выделить, следующие подходы к определению понятия «информация».
|
|
|
В философии слово «информация» связано с понятиями взаимодействие, отражение, познание.
В кибернетике (науке об управлении) слово «информация» используется для характеристики управляющего сигнала, передаваемого по линии связи, как мера уменьшения неопределенности в системе управления.
В повседневной практике слово «информация» применяется как синоним слов сведения, знания, сообщения.
Юридическая деятельность осуществляется в сфере социальных систем и явлений, то есть в сфере отношений между людьми. Поэтому в этой сфере естественно использовать тот смысл термина «информация», который отвечает двум последним подходам и определен ст. 2 Федерального Закона "Об информации, информационных технологиях и о защите информации":
информация – сведения(сообщения, данные) независимо от формы их представления.
24. Основные закономерности создания и функционирования информационных процессов. Формы представления информации.
Наличие информации, ее своевременное получение является необходимым условием эффективного управления сложными динамическими объектами и их отношениями. Вместе с тем информация, циркулирующая в эргасистемах, то есть в сложных человеко-машинных системах управления (в частности, и в системах правового регулирования), является критическим компонентом, способным вызвать крупномасштабные аварии, вооружённые конфликты, дезорганизацию деятельности научно-исследовательских учреждений и испытательных центров, разорение банков и коммерческих организаций. Информация может представлять государственную, служебную, профессиональную, коммерческую, семейную и личную тайну. Она становится товаром, имеющим цену, автора, гарантии качества. Существующие естественные (случайные) и искусственные (преднамеренные) угрозы нарушения её достоверности, сохранности и конфиденциальности обусловливают жизненно важную необходимость создания эффективных мер контроля всевозможных угроз и защиты информации в эргасистемах от искажения при переработке, от разрушения при эксплуатации, а также от раскрытия (утечки) и вредоносной модификации.
|
|
|
В сфере юриспруденции применяются две формы представления информации.
Вербальная (словесная) форма, когда сведения задаются устной или письменной речью. Она используется для качественной характеристики объектов и процессов. Такая форма фиксации и передачи информации принята в большинстве правовых актов.
Числовая форма (форма данных), – когда сведения задаются количественными характеристиками объектов и процессов. А эти характеристики получены путем измерений, наблюдений, путем обработки их результатов с помощью логических или арифметических операций. Так результаты измерения и анализа состояния преступности в РФ сводятся в таблицы и регулярно публикуются Федеральной службой государственной статистики и Судебным департаментом при Верховном Суде РФ.
Современные информационные технологии реализуются на компьютерах. И вся информация в компьютерах представлена в числовой форме, а именно, двоичными кодами.
25. Причины вероятностного характера информационных процессов в системах коммуникации, понятия энтропии и количества информации.
Отметим, что каждый из двух первых информационных процессов (производство и интерпретация информации) начинаются и завершаются третьим, а именно, коммутацией информации. Коммутация информации – это передача ее в пространстве по каналам связи или во времени посредством хранения на носителях. При передаче информации в пространстве стремятся минимизировать время передачи, а при передаче ее во времени минимизируют пространство (объем носителя).
L t1UKDXHTtVBSKC5JzEtJzMnPS7VVqkwtVrK34+UCAAAA//8DAFBLAwQUAAYACAAAACEAFToxV8cA AADdAAAADwAAAGRycy9kb3ducmV2LnhtbESPQWsCMRSE7wX/Q3iCl1KzLkVlNYoKQgsV0Yrnx+Z1 s3Xzsm5SXfvrm4LgcZiZb5jpvLWVuFDjS8cKBv0EBHHudMmFgsPn+mUMwgdkjZVjUnAjD/NZ52mK mXZX3tFlHwoRIewzVGBCqDMpfW7Iou+7mjh6X66xGKJsCqkbvEa4rWSaJENpseS4YLCmlaH8tP+x Csa3183zcTg6flfb96X5Lc78cUKlet12MQERqA2P8L39phWko0EK/2/iE5CzPwAAAP//AwBQSwEC LQAUAAYACAAAACEA8PeKu/0AAADiAQAAEwAAAAAAAAAAAAAAAAAAAAAAW0NvbnRlbnRfVHlwZXNd LnhtbFBLAQItABQABgAIAAAAIQAx3V9h0gAAAI8BAAALAAAAAAAAAAAAAAAAAC4BAABfcmVscy8u cmVsc1BLAQItABQABgAIAAAAIQAzLwWeQQAAADkAAAAQAAAAAAAAAAAAAAAAACkCAABkcnMvc2hh cGV4bWwueG1sUEsBAi0AFAAGAAgAAAAhABU6MVfHAAAA3QAAAA8AAAAAAAAAAAAAAAAAmAIAAGRy cy9kb3ducmV2LnhtbFBLBQYAAAAABAAEAPUAAACMAwAAAAA= " stroked="f" strokeweight=".5pt">
| Рис. В.1 |
| СИСТЕМА КОММУНИКАЦИИ |
| ВХОДНОЙ ИМ |
| ВЫХОДНОЙ ИМ |
| ПОМЕХИ |
Главная задача системы коммутации (рис. В.1) состоит в том, чтобы в достаточной мере обеспечить взаимно-однозначное соответствие между информационными массивами ИМ на ее входе и на ее выходе. Нарушение этого соответствия обусловлено неизбежными помехами той или иной природы, которые воздействуют на систему коммутации. Этим определяется вероятностный характер процессов в системе коммутации. Научной базой для исследования процессов коммуникации является теория информации, фундаментальные положения которой разработал американский инженер и математик К. Шеннон в 1948 г. Ознакомимся с основными понятиями этой теории.
|
|
|
| Таблица В.1 | ||
| i | xi | p(xi) |
| x1 | p(x1) | |
| x2 | p(x2) | |
| ¼ | ¼ | ¼ |
| N | xN | p(xN) |
26. Содержание меры энтропии по Шеннону и связь этой меры с мерой энтропии по Хартли. Единицы измерения энтропии. Свойства энтропии. Практический пример.
Рассмотрим конечное множество X случайных событий x1,x2,…,xN. Случайным событием может быть появление на входе (на выходе) системы коммутации того или иного элемента входного (выходного) информационного массива. Любые действия, приводящие к наступлению события xi, i=1,2,…,N= 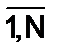 , называют опытом или испытанием. Получение информации в опыте связано с тем, что до его осуществления имеется известная неопределенность в его исходе. По окончании испытания наступает одно из N событий. Тем самым неопределенность относительно результатов опыта уменьшается (а может быть, и полностью исчезает). Это уменьшение неопределенности относительно результатов испытания после его осуществления и понимают как получение информации. Обозначим количественную меру неопределенности до опыта как Hдо опыта, а количественную меру оставшейся неопределенности как Hпосле опыта. Тогда количественной мерой информации I(X) в опытах с множеством X будет разность
, называют опытом или испытанием. Получение информации в опыте связано с тем, что до его осуществления имеется известная неопределенность в его исходе. По окончании испытания наступает одно из N событий. Тем самым неопределенность относительно результатов опыта уменьшается (а может быть, и полностью исчезает). Это уменьшение неопределенности относительно результатов испытания после его осуществления и понимают как получение информации. Обозначим количественную меру неопределенности до опыта как Hдо опыта, а количественную меру оставшейся неопределенности как Hпосле опыта. Тогда количественной мерой информации I(X) в опытах с множеством X будет разность
I(X)=Hдо опыта-Hпосле опыта. (В.1)
|
|
|
Обычно множество X задают так (табл. В.1). Здесь p(xi) – вероятность наступления события xi. Эти вероятности отвечают условию
p(x1)+p(x2)+¼+p(xN)=1. (В.2)
Количественной мерой неопределенности в опытах с конечным множеством случайных событий X является величина H(X), которая называется энтропией:
H(X)=-(p(x1)´loga(p(x1))+p(x2)´loga(p(x2))+¼+p(xN)´loga(p(xN))).
В математике длинную цепочку слагаемых ради экономии места заменяют такой конструкцией:
H(X)= 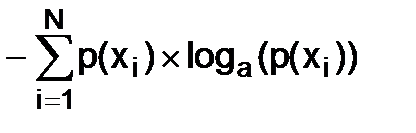 . (В.3)
. (В.3)
Формула (В.3) выведена К. Шенноном.
Перечислим свойства энтропии.
1. Энтропия равна нулю, если в любом опыте с множеством X исход известен заранее: всегда наступает событие xj и никогда не происходят события xi, i¹j. Неопределенность в таком опыте отсутствует. А отсутствие неопределенности означает, что энтропия равна нулю.
2. Величина H(X) зависит от вероятностей p(xi) и достигает максимального значения тогда, когда события xi равновероятны:
p(x1)=p(x2)=¼=p(xN)=p.
И эти вероятности отвечают условию (В.2):N´p=1. Поэтому p= 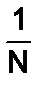 .
.
В этом случае
H(X)=  =áN одинаковых слагаемыхñ=
=áN одинаковых слагаемыхñ=
=-N´  =loga(N).
=loga(N).
Формулу
H(X)=loga(N) (В.4)
для энтропии множества равновероятных событий вывел в 1928 г. американский инженер Р. Хартли. Это была первая попытка количественной оценки энтропии.
3. Если в опыте одновременно участвуют и множество X с энтропией H(X), и множество Y с энтропией H(Y), то есть оперируют с множеством X´Y, то энтропия H(X´Y) такого множества равна
H(X´Y)=H(X)+H(Y). (В.5)
Формула (В.5) справедлива для любого числа k слагаемых. А если все они одинаковы, то есть оперируют с множеством Xk, и
H(Xk)=k´H(X).
Основание a логарифма в формулах (В.3) и (В.4) определяет единицу измерения энтропии. Действительно,
H(X)=loga(N)=1
тогда, когда a=N. В настоящее время общепринято использование в формулах (В.3) и (В.4) значения a=N=2, что хорошо согласуется с формальной логикой и двоичным кодированием информации. А единицей измерения энтропии при a=2 является бит (англ. bit от сжатия слов binary digit). История науки знает случаи использования и таких единиц, как нит (a=e) и дит (a=10). Один бит равен 1.44 нит (log2(e)) или 3.32 дит (log2(10)).
| Таблица В.2 | ||
| i | xi | p(xi) |
| 0.1250 | ||
| 0.1250 | ||
| 0.1250 | ||
| 0.0179 | ||
| 0.1250 | ||
| 0.0179 | ||
| 0.1250 | ||
| 0.0179 | ||
| 0.0179 | ||
| 0.1250 | ||
| 0.0179 | ||
| 0.1250 | ||
| 0.0179 | ||
| 0.0179 |
 Пример. Пусть некто первый случайным образом загадывает целое число из диапазона X=[0,15]. При этом он никогда не загадывает круглые числа, а предпочтение отдает простым числам (табл. В.2). Вычислим энтропию такого множества случайных событий. В этом случае необходимо применить меру Шеннона (В.3) для N=16. Вычисляем сначала log2(p(xi)), потом произведения p(xi)´log2(p(xi)). Далее суммируем эти произведения, знак суммы инвертируем и получаем
Пример. Пусть некто первый случайным образом загадывает целое число из диапазона X=[0,15]. При этом он никогда не загадывает круглые числа, а предпочтение отдает простым числам (табл. В.2). Вычислим энтропию такого множества случайных событий. В этом случае необходимо применить меру Шеннона (В.3) для N=16. Вычисляем сначала log2(p(xi)), потом произведения p(xi)´log2(p(xi)). Далее суммируем эти произведения, знак суммы инвертируем и получаем
|
|
|
H(X)=3.351 бита.
Изменим условие задачи так. Некто первый не отдает предпочтения ни одному из этих чисел. Вычислим энтропию множества X. В данном случае, как и ранее, N=16, но все исходы загадывания равновероятны: p= 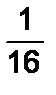 , и для вычисления энтропии воспользуемся мерой Хартли (В.4):
, и для вычисления энтропии воспользуемся мерой Хартли (В.4):
H(X)=log2(16)=4 бита.
Как видим, энтропия множества неравновероятных событий меньше энтропии множества равновероятных событий.
Пусть загадано число 13, и некто второй должен определить загаданное число. Покажем, что для этого достаточно задать первому четыре вопроса (табл. В.3). Как видим, после ответа на каждый вопрос диапазон чисел, среди которых и загаданное, уменьшается вдвое, и после четвертого вопроса остается одно загаданное число.
Вычислим, какое количество информации получено после ответа на первый вопрос. До ответа на первый вопрос имеем
Hдо опыта=H(X)=4 бита.
Ответ на первый вопрос показал, что задуманное число находится во второй половине диапазона [0,15]. Значит, вероятности для чисел из первой его половины равны нулю, а вероятности для чисел из второй половины удвоились (сумма вероятностей для всех чисел отвечает условию (В.2)). Энтропию такого множества неравновероятных событий следует вычислять по формуле Шеннона (В.3). Учтем, что в сумме (В.3) первые восемь слагаемых равны нулю, потому что у них p(xi)=0 (см. табл. В.3).
Поэтому 
Hпосле опыта= 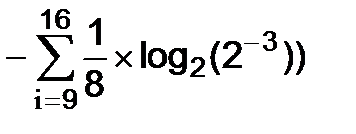 =áвосемь одинаковых слагаемыхñ=
=áвосемь одинаковых слагаемыхñ=
= 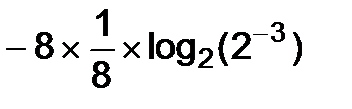 =3 бита.
=3 бита.
Значит, количество информации, полученное после ответа на первый вопрос, равно
I(X)=Hдо опыта-Hпосле опыта=4-3=1 бит.
После ответа на четвертый вопрос остается только искомое число с вероятностью, равной 1, то есть Hпосле опыта=0. Значит, полная информация, полученная в ответах на четыре вопроса, составит
I(X)=H(X)=4 бита.
 Пример. Из 32 символов множества X составляют сообщения из трех символов. Какое количество информации несет такое сообщение?
Пример. Из 32 символов множества X составляют сообщения из трех символов. Какое количество информации несет такое сообщение?
Здесь множество случайных событий X мощностью N=32. Ни один из символов не имеет преимуществ перед другими, то есть все они равновероятны в одной выборке.
| Таблица В.3 | ||||||
| Вопрос | - | >7? | >11? | >13? | >12? | |
| Ответ | - | Да. | Да. | Нет. | Да. | |
| i | xi | p(xi) | p(xi) | p(xi) | p(xi) | p(xi) |
| 0.0625 | ||||||
| 0.0625 | ||||||
| 0.0625 | ||||||
| 0.0625 | ||||||
| 0.0625 | ||||||
| 0.0625 | ||||||
| 0.0625 | ||||||
| 0.0625 | ||||||
| 0.0625 | 0.1250 | |||||
| 0.0625 | 0.1250 | |||||
| 0.0625 | 0.1250 | |||||
| 0.0625 | 0.1250 | |||||
| 0.0625 | 0.1250 | 0.2500 | 0.5000 | |||
| 0.0625 | 0.1250 | 0.2500 | 0.5000 | 1.0000 | ||
| 0.0625 | 0.1250 | 0.2500 | ||||
| 0.0625 | 0.1250 | 0.2500 | ||||
| H(X) | ||||||
| I(X) |
Значит, энтропия множества X при выборе одного символа вычисляется по формуле Хартли:
H(X)=log2(N)=log2(32)=5 битов.
При выборе трех символов множество X используется k=3 раза, то есть в сообщении из трех символов оперируют с множеством X3, а элементом этого множества является любое сообщение. В соответствии со свойством 3 энтропия множества X3 равна
H(X3)=3´H(X)=15 битов.
До составления того или иного сообщения неопределенность в исходе этого опыта есть
Hдо опыта=H(X3))=15 битов.
После формирования конкретного сообщения неопределенность в исходе опыта отсутствует. А это означает, что
Hпосле опыта=0.
Значит,
I(X)=Hдо опыта-Hпосле опыта=15 битов.
Отметим, что общее количество k-символьных сообщений, которые можно составить из N символов равно Nk, потому что в каждую из k позиций для сообщения можно поместить любой из N символов В нашем примере из 32 символов можно составить 323=32768 трехсимвольных сообщений.
27. Условная энтропия. Пояснить с помощью диаграмм Венна энтропийно-информационные оценки в системах коммуникации. Практический пример.
В системе коммутации оперируют с двумя массивами случайных событий. Это входной информационный массив X с энтропией H(X) и выходной информационный массив Y с энтропией H(Y). С системой коммутации связаны также понятия условных энтропий H(X½Y), H(Y½X) и количества информации I(X,Y).
H(X½Y) – условная энтропия множества X, когда на выходе системы имеет место множество Y. Она характеризует неопределенность X, которая остается после приема Y, то есть потерю информации из-за влияния помех:
I(X,Y)=H(X)-H(X½Y). (В.6)
H(Y½X) – условная энтропия множества Y, когда на входе системы имеет место множество X. Она характеризует неопределенность множества Y, которая остается после передачи X, то есть информацию о множестве X в принятом Y в условиях помех:
I(X,Y)=H(Y)-H(Y½X). (В.7)
Диаграммы Венна (рис. В.2) – наглядная иллюстрация соотношений между данными энтропийно-информационными понятиями системы коммутации
| Рис. В.2 |

| H(X½Y) |

| H(Y½X) |
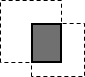
| I(X,Y) |
| H(X) |
| H(Y) |
.
 Пример. Рассмотрим простейшую систему коммуникации, в которой входной информационный массив X задан символами x1=0, x2=1, а выходной – символами y1=0, y2=1. Положим, что вероятность ошибки при приеме символа равна p, а вероятность безошибочного приема символа равна 1-p.
Пример. Рассмотрим простейшую систему коммуникации, в которой входной информационный массив X задан символами x1=0, x2=1, а выходной – символами y1=0, y2=1. Положим, что вероятность ошибки при приеме символа равна p, а вероятность безошибочного приема символа равна 1-p.
| Рис. В.3 |
| СИСТЕМА КОММУНИКАЦИИ |
| ВЫХОДНОЙ ИМ |
| ВХОДНОЙ ИМ |
| x1 |
| x2 |
| y1 |
| y2 |
| p |
| p |
| 1-p |
| 1-p |
На рис. В.3 схематически показана такая система коммуникации. Стрелки показывают, в какие символы множества Y и с какой вероятностью переходит каждый из символов множества X. В теории информации такая система коммуникации называется двоичным симметричным каналом связи.
Вычислять количество информации I(X,Y) будем по формуле (В.7), в которой энтропия H(Y) имеет максимально возможное значение H(Y)=1, а условная энтропия H(Y½X) определяется соотношением (дается без вывода)
H(Y½X)=-(p´log2(p)+(1-p)´log2(1-p)). (В.8)
Тогда
I(X,Y)=1-H(Y½X)=1+(p´log2(p)+(1-p)´log2(1-p)) (В.9).
L t1UKDXHTtVBSKC5JzEtJzMnPS7VVqkwtVrK34+UCAAAA//8DAFBLAwQUAAYACAAAACEAgTDL2sgA AADdAAAADwAAAGRycy9kb3ducmV2LnhtbESPQUvDQBSE74L/YXkFL8VuqjaWtNtShYKCUqyl50f2 NRubfRuza5P017tCweMwM98w82VnK3GixpeOFYxHCQji3OmSCwW7z/XtFIQPyBorx6SgJw/LxfXV HDPtWv6g0zYUIkLYZ6jAhFBnUvrckEU/cjVx9A6usRiibAqpG2wj3FbyLklSabHkuGCwpmdD+XH7 YxVM+4f34T593H9Vm9cncy6++e2ISt0MutUMRKAu/Icv7Ret4D5NJvD3Jj4BufgFAAD//wMAUEsB Ai0AFAAGAAgAAAAhAPD3irv9AAAA4gEAABMAAAAAAAAAAAAAAAAAAAAAAFtDb250ZW50X1R5cGVz XS54bWxQSwECLQAUAAYACAAAACEAMd1fYdIAAACPAQAACwAAAAAAAAAAAAAAAAAuAQAAX3JlbHMv LnJlbHNQSwECLQAUAAYACAAAACEAMy8FnkEAAAA5AAAAEAAAAAAAAAAAAAAAAAApAgAAZHJzL3No YXBleG1sLnhtbFBLAQItABQABgAIAAAAIQCBMMvayAAAAN0AAAAPAAAAAAAAAAAAAAAAAJgCAABk cnMvZG93bnJldi54bWxQSwUGAAAAAAQABAD1AAAAjQMAAAAA " stroked="f" strokeweight=".5pt">
| Рис. В.4 |
| 0.25 |
| 0.50 |
| 0.75 |
| 0.75 |
| 0.25 |
| 1.00 |
| 0.50 |
| 0.00 |
| p |
| I(X,Y) |
| H(Y½X) |
На рис. В.4 показаны графики H(Y½X) и I(X,Y), построенные по формулам (В.8) и (В.9). Как видим, с увеличением p от 0 до 0.5 условная энтропия H(Y½X) возрастает, а количество информации в массиве Y относительно массива X падает.
При p=0.5 оказывается, что H(Y½X)=1, а I(X,Y)=0. Объясняется это тем, что при p=0.5 теряется зависимость между символами массивов X и Y. Когда передается символ x1=0, на выходе с равной вероятностью принимается или символ y1=0, или символ y2=1. То же самое имеет место и при передаче символа x2=1. Значит, при p=0.5 неопределенность выходного массива Y при известном входном массиве X максимальна, и элементы массива Y не содержат никакой информации о символах массива X.
С увеличением p от 0.5 до 1 условная энтропия H(Y½X) падает, а количество информации I(X,Y) растет. Передача символа x1=0 чаще всего вызывает появление на выходе символа y2=1, а при передаче x2=1 на выходе чаще всего будет y1=0. Если при p>0.5 выполнять инверсию символов на выходе (замену нуля на единицу, а единицы на нуль), то вероятность искажения результата инверсии будет равна 1-p<0.5.
28. Оценка скорости передачи информации. Практический пример.
Важной характеристикой системы коммуникации является скорость передачи информации. Она определяет временные затраты на процедуру обмена информацией. Положим, что входной информационный массив представляет собою последовательность символов, которая разворачивается во времени. Если средняя длительность одного символа в такой последовательности составляет tср, то скорость передачи информации vи составит
vи= 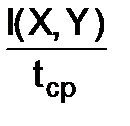 .
.
Размерностью для vи будет 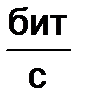 =бод.
=бод.
Дальнейшее развитие информационных технологий, обусловленное достижениями научно-технического прогресса, создает предпосылки для создания и совершенствования базовых структур наступающего информационного общества, таких как электронное правительство, электронный парламент, электронное правосудие и др.
Внедрение в правовые эргасистемы современных эффективных информационных технологий требует больших материальных затрат как на разработку наукоемкой информационной техники и программно-алгоритмического обеспечения, так и на подготовку специалистов технического, информационного и информационно-правового профиля.
ЭЛЕМЕНТЫ СТАТИСТИЧЕСКОЙ ОБРАБОТКИ ДАННЫХ
29. Понятие абсолютной и относительной величины. Проценты. Практический пример.
При исследовании того или иного социального явления (например, преступности) важную роль играют сбор и обработка статистических данных, которые несут информацию об этом явлении. Цель обработки данных состоит в получении обобщающих характеристик изучаемого явления. В юридической статистике разработана целая система обобщающих характеристик. Здесь мы остановимся только на таких показателях, которые представлены абсолютными и относительными величинами.
Абсолютная величина – количественная характеристика объема (размера) изучаемого явления в определенных временных и/или пространственных границах. Абсолютную величину получают путем суммирования статистических данных об изучаемом явлении. Абсолютная величина всегда именованное число, то есть имеет размерность, связанную с принятой единицей измерения. Отметим, что в статистике термин «абсолютная» не имеет толкования «модуль» в математике. В статистике абсолютная величина может быть и отрицательной.
Одна из основных операций при анализе статистических данных – сравнение числовых величин, характеризующих изучаемое явление. Непосредственное сравнение абсолютных величин, характеризующих это явление в различные моменты времени или в разных точках пространства, не всегда приводит к верным выводам (см. табл. 2.3 ниже). Более продуктивным оказывается сравнение относительных величин.
Относительная величина – количественная мера соотношения двух абсолютных величин, одна из которых принимается за базу сравнения. Вычисляют относительную величину путем деления сравниваемой абсолютной величины на базу сравнения. Ниже рассматриваем только отношение абсолютных величин, имеющих одну и ту же размерность. Полученная так относительная величина характеризует распределение исследуемого явления в пространстве или развитие его во времени.
В тех случаях, когда модуль отношения абсолютных величин лежит в пределах [~10-3, ~5], относительную величину удобно выражать в процентах. Для этого базе сравнения B ставят в соответствие 100%, а сравниваемой абсолютной величине A отвечают A%. Так составляют пропорцию
 =
= 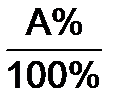 ,
,
которая лежит в основе всех операций с процентами.
Когда заданы величины A и В, то A% вычисляют так:
A%=  %. (2.4)
%. (2.4)
| Таблица 2.3 | |||
| Регион | П – число лиц, совершивших преступления (тыс. чел) | Н – население (тыс. чел) | П%= 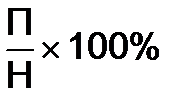
|
| Тамбовская обл. | 9.22 | 1088.44 | 0.85% |
| Тульская обл. | 9.54 | 1540.38 | 0.62% |
 Пример. По данным Федеральной службы государственной статистики за 2009 год составлена табл. 2.3.
Пример. По данным Федеральной службы государственной статистики за 2009 год составлена табл. 2.3.
Сравнение абсолютных величин П приводит к выводу о том, что положение с преступностью в Тульской обл. хуже, чем в Тамбовской. Однако сравнение относительных величин П%, полученных по формуле (2.4), дает противоположный результат, который и отвечает фактическому состоянию преступности в этих регионах.
Когда же заданы значения A% и В, величину A находят так:
A=B´ 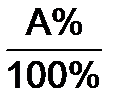 . (2.5)
. (2.5)
 Пример. В 2009 году число лиц (тыс.), совершивших преступления в России, оказалось равным 1219.8. Из них 15.9% – женщины. Абсолютное число женщин найдем по формуле (2.5):
Пример. В 2009 году число лиц (тыс.), совершивших преступления в России, оказалось равным 1219.8. Из них 15.9% – женщины. Абсолютное число женщин найдем по формуле (2.5):
женщины:  =193.9.
=193.9.
А если заданы A и A%, то базу B находят по формуле
B=A´  . (2.5)
. (2.5)
 Пример. В 2009 году в РФ осуждено лиц (тыс.) 892.2, что составило 73.1% от числа лиц, совершивших преступления в России в этом же году. По формуле (2.5) найдем число лиц, совершивших преступления в России в 2009 году:
Пример. В 2009 году в РФ осуждено лиц (тыс.) 892.2, что составило 73.1% от числа лиц, совершивших преступления в России в этом же году. По формуле (2.5) найдем число лиц, совершивших преступления в России в 2009 году:
892.2´ 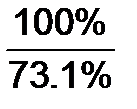 =1220.5.
=1220.5.
Полученный результат 1220.5¹1219.8 (см. выше) обусловлен погрешностями округления и абсолютных, и относительных величин.
30. Расчет темпов роста и темпов прироста при базисном способе вычисления Практический пример.
31. Понятие абсолютной и относительной величины. Расчет темпов роста и темпов прироста при цепном способе вычисления. Практический пример.
Рассмотрим еще две относительные величины, которые характеризуют развитие изучаемого явления в заданном временном интервале и которые тоже выражаются в процентах. В этом случае задана таблица, в первой строке которой приведены отсчеты времени Ti (месяцы, годы), а во второй – значения абсолютных величин Ai в эти моменты времени (i= 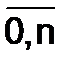 ). Тогда динамика развития исследуемого явления на интервале от T0 до Tn характеризуется его темпом роста и темпом прироста.
). Тогда динамика развития исследуемого явления на интервале от T0 до Tn характеризуется его темпом роста и темпом прироста.
Темп роста ТРi – выраженное в процентах отношение абсолютной величины Ai в данный момент к базовой величине AБ.
Темп прироста ТПi – выраженное в процентах отношение разности Ai-AБ абсолютной величины в данный момент времени и базовой величины к базовой величине AБ.
Применяют два способа вычисления названных показателей динамики: базисный и цепной. Различаются они заданием базовой величины AБ.
Базисный способ. В этом случае величина AБ одна и та же для всех моментов времени. Обычно в качестве базы выступает значение абсолютной величины в начальный момент времени: AБ=A0. Тогда базисным способом темп роста ТРБi и темп прироста ТПБi вычисляют так:
ТРБi=  , i=
, i= 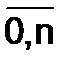 .
.
ТПБi= 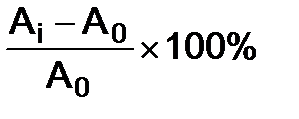 =ТРБi-100%, i=
=ТРБi-100%, i= 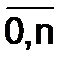 .
.
| Таблица 2.4 | |||||
| i | |||||
| Ti | |||||
| Ai | |||||
| ТРБi% | 100.00 | 105.00 | 113.10 | 118.78 | 108.58 |
| ТПБi% | +05.00 | +13.10 | +18.78 | +08.58 |
 Пример. В табл. 2.4 приведены вычисленные базисным способом показатели динамики числа таких преступлений в РФ за 2006-2010 годы, как взяточничество.
Пример. В табл. 2.4 приведены вычисленные базисным способом показатели динамики числа таких преступлений в РФ за 2006-2010 годы, как взяточничество.
Как видим, к 2009 года количество таких преступлений как взяточничество в РФ выросло по отношению 2006 году на 18.78%. А в 2010 году оно снизилось и составило 108.58% от уровня 2006 года.
Цепной способ. В этом случае величина AБ – переменная. Для данного момента времени она равна значению абсолютной величины в предыдущий момент времени: AБ=Ai-1. Тогда цепным способом темп роста ТРЦi и темп прироста ТПЦi вычисляют так:
ТРЦi= 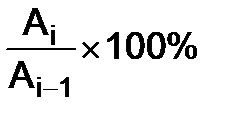 , i=
, i=  .
.
ТПЦi= 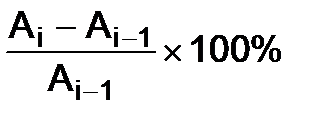 =ТРЦi-100%, i=
=ТРЦi-100%, i= 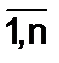 .
.
| Таблица 2.5 | |||||
| i | |||||
| Ti | |||||
| Ai тыс. | |||||
| ТРЦi% | - | 105.00 | 107.71 | 105.03 | 91.41 |
| ТПЦi% | - | +05.00 | +07.71 | +05.03 | -08.59 |
 Пример. В табл. 2.5 приведены вычисленные цепным способом показатели динамики числа таких преступлений в РФ за 2006-2010 годы, как взяточничество.
Пример. В табл. 2.5 приведены вычисленные цепным способом показатели динамики числа таких преступлений в РФ за 2006-2010 годы, как взяточничество.
Как видим, с 2006 до 2009 года количество таких преступлений как взяточничество в РФ росло от года к году на 5-7 процентов. А в 2010 году оно уменьшилось на 8.59% по отношению к 2009 году.
32. Понятие закона распределения случайной величины. Законы распределения дискретных случайных величин. Ряд распределения. Практический пример.
Законы распределения случайных величин
Всякое соотношение, которое устанавливает связь между возможными значениями случайной величины и вероятностями этих значений, называют законом распределения этой СВ.
Изучение законов распределения начнем с дискретных случайных величин.
Ряд распределения. Обозначим дискретную СВ как X, а набор ее отсчетов – как x0, x1,…, xn. Исход случайного эксперимента – событие X=xk характеризуется вероятностью P(X=xk)=pk. Факт равенства чисел X=xk устанавливают путем последовательного сравнения цифр в одноименных разрядах записей X и xk (см. рис. 8.2). Если имеет место ai=bi для всех i=r,r-1,¼,-m, то числа X и xk равны.
| X= |
| ar |
| ar-1 |
| ¼ |
| a0. |
| a-1 |
| ¼ |
| a-m+1 |
| a-m |
| xk= |
| br |
| br-1 |
| ¼ |
| b0. |
| b-1 |
| ¼ |
| b-m+1 |
| b-m |
| = |
| = |
| = |
| = |
| = |
| = |
| ¼ |
| ¼ |
| Рис. 8.2 |
Сопоставим каждому отсчету xk случайной величины X вероятность pk. В результате получим закон распределения дискретной СВ X. Самой простой формой записи закона распределения дискретной случайной величины является таблица, в первой строке которой перечисляются ее отсчеты xk, а во второй – вероятности pk. Такую таблицу {xk,pk} и называют рядом распределения.
Очевидн
|
|
|


