 |
Глава 2. Распределение Гиббса.
|
|
|
|
Глава 2. Распределение Гиббса.
§2. 1. Канонический ансамбль. Распределение Гиббса.
Канонический ансамбль – это совокупность незамкнутых систем. Каждая из этих систем является частью большой замкнутой системы.
Найдем функцию распределения систем канонического ансамбля по энергиям
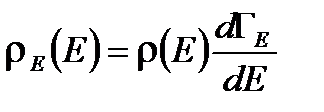 . (2. 1)
. (2. 1)
Эта функция была введена для некоторого макроскопического равновесного тела (подсистемы), помещенного в окружающую среду (резервуар) и составляющего с этой средой замкнутую систему. Взаимодействие такого тела с окружающей средой слабое и в полном балансе энергий им можно пренебречь. Полная энергия замкнутой системы равна
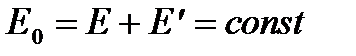 , (2. 2)
, (2. 2)
где E - энергия тела (подсистемы), E' - энергия резервуара.
|
|
Рис. 2. 1. Замкнутая система, состоящая из маленькой подсистемы и резервуара.
Пусть размер подсистемы (тела) значительно меньше размера системы, т. е. E' > > E. Для числа частиц в полной системе и подсистеме имеет место условие  . Так как в макроскопических телах флуктуации энергии в состоянии равновесия малы, то можно считать, что энергия среды E' есть среднее значение энергии
. Так как в макроскопических телах флуктуации энергии в состоянии равновесия малы, то можно считать, что энергия среды E' есть среднее значение энергии 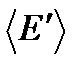 . В дальнейшем знак усреднения
. В дальнейшем знак усреднения 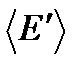 писать больше не будем, всегда подразумевая средние значения энергии для больших систем в равновесии.
писать больше не будем, всегда подразумевая средние значения энергии для больших систем в равновесии.
Нас интересует вероятность 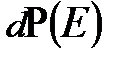 такого состояния подсистемы, в котором тело находится в состоянии с энергией от E до E + dE, а окружающая среда - в равновесном макроскопическом состоянии со средней энергией E'. Это состояние среды можно описать фазовым объемом
такого состояния подсистемы, в котором тело находится в состоянии с энергией от E до E + dE, а окружающая среда - в равновесном макроскопическом состоянии со средней энергией E'. Это состояние среды можно описать фазовым объемом 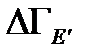 . Напомним, что
. Напомним, что 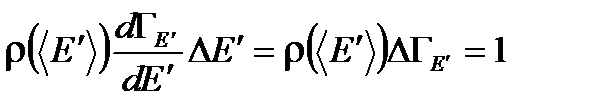 , а статистический вес состояния равен
, а статистический вес состояния равен 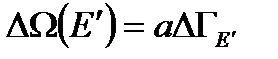 . Фазовый объем
. Фазовый объем 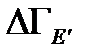 пропорционален числу способов распределения энергии
пропорционален числу способов распределения энергии 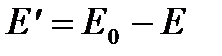 по окружающей среде. Так как тело и среда статистически независимы, то вероятность
по окружающей среде. Так как тело и среда статистически независимы, то вероятность 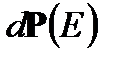 пропорциональна произведению фазового объема состояния тела
пропорциональна произведению фазового объема состояния тела 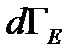 и фазового объема макроскопического состояния окружающей среды
и фазового объема макроскопического состояния окружающей среды 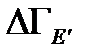
|
|
|
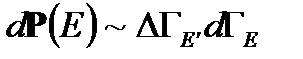 . (2. 3)
. (2. 3)
Фазовый объем макроскопического состояния среды можно выразить через энтропию окружающей среды - 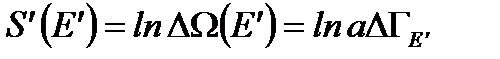 .
.
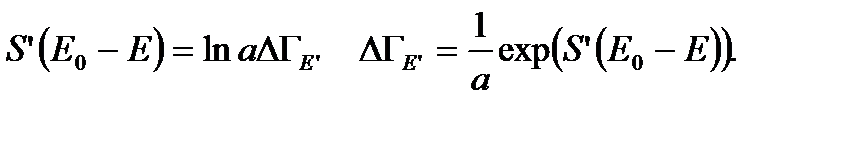
Подставляя последнее выражение в (2. 3), получаем:
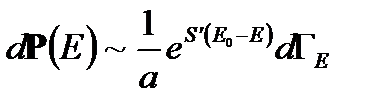 (2. 4)
(2. 4)
Учтем, что тело составляет малую часть системы, т. е. Е < < E0. Разложим энтропию среды S'(E0-E) в ряд в окрестности точки E0:
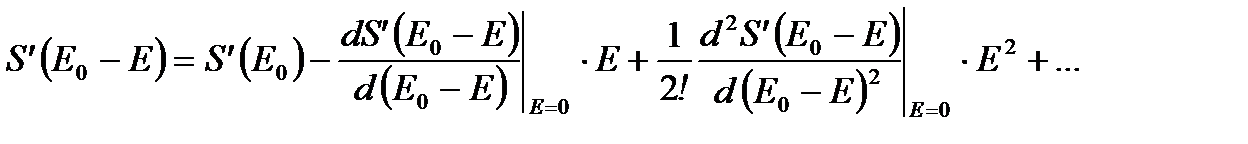 (2. 5)
(2. 5)
и ограничимся первым порядком в разложении по энергии Е.
Обозначив
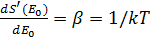 , (2. 6)
, (2. 6)
где k- постоянная Больцмана, T- абсолютная температура, получаем
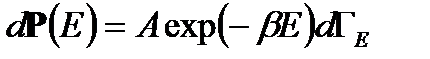 . (2. 7)
. (2. 7)
Здесь Е - энергия изучаемого тела, зависящая от координат и скоростей составляющих его атомов или молекул. Постоянную А можно найти из условия нормировки 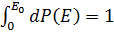 . Из (2. 7) получаем
. Из (2. 7) получаем
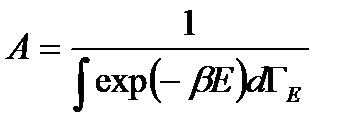 (2. 8)
(2. 8)
Сравнивая выражение (2. 7) с 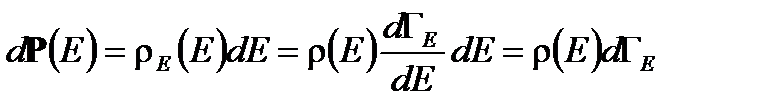 , получаем плотность вероятности - функцию статистического распределения
, получаем плотность вероятности - функцию статистического распределения
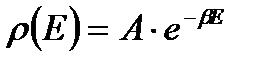 (2. 9)
(2. 9)
Это и есть распределение Гиббса. Формула (2. 9) дает распределение вероятностей различных микроскопически х состояний подсистемы, являющейся малой частью некоторой большой замкнутой системы.
§2. 2. Распределение Максвелла и его свойства.
В классической физике полная энергия всегда может быть разделена на кинетическую K и потенциальную U энергии
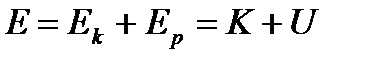 , (2. 10)
, (2. 10)
где K - функция скоростей, U - функция координат. Функция U, вообще говоря, состоит из потенциальной энергии взаимодействия атомов между собой и из потенциальной энергии во внешнем поле. При этом элемент фазового объема можно представить в виде произведения двух элементов
|
|
|
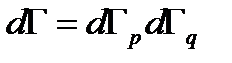 , (2. 11)
, (2. 11)
где 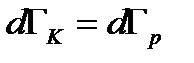 элемент фазового объема в пространстве импульсов (скоростей),
элемент фазового объема в пространстве импульсов (скоростей), 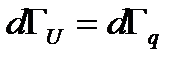 фазовый объем в пространстве координат. Тогда вероятность записывается
фазовый объем в пространстве координат. Тогда вероятность записывается
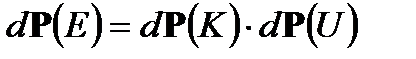 (2. 12)
(2. 12)
Такое разбиение вероятности 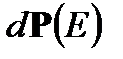 на два независимых сомножителя означает, что вероятность иметь определенные значения для кинетической энергии никак не влияет на вероятность иметь какие-то значения для потенциальной энергии. Поэтому вероятности
на два независимых сомножителя означает, что вероятность иметь определенные значения для кинетической энергии никак не влияет на вероятность иметь какие-то значения для потенциальной энергии. Поэтому вероятности 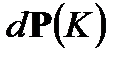 и
и 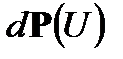 должны удовлетворять независимым условиям нормировки для определения постоянных a и b:
должны удовлетворять независимым условиям нормировки для определения постоянных a и b:
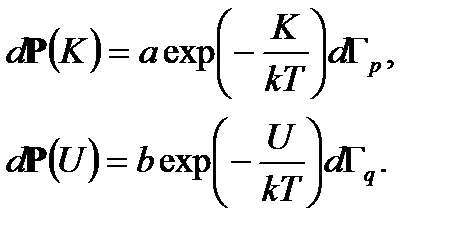 (2. 13)
(2. 13)
Такое разбиение распределения по полным энергиям на два независимых распределения по кинетическим и потенциальным энергиям возможно лишь в классической физике . При квантовом рассмотрении вероятности различных значений координат и импульсов оказываются связанными друг с другом за счет соотношения неопределенностей.
|
|
|



