 |
§3.2.Идеальный газ Бозе - Эйнштейна.
|
|
|
|
§3. 2. Идеальный газ Бозе - Эйнштейна.
Рассмотрим систему невзаимодействующих бозонов, находящихся в объеме V. В соответствии с (3. 1) запишем статистическую сумму в явном виде
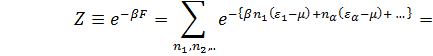
 (
( 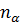 =0, 1, 2, 3, …. ) (3. 13)
=0, 1, 2, 3, …. ) (3. 13)
Каждый из сомножителей (бесконечных рядов) в этом выражении равен
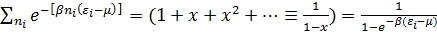 . (3. 14)
. (3. 14)
Для статсуммы и свободной энергии имеем:
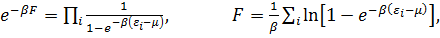 (3. 15)
(3. 15)
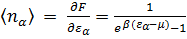 . (3. 16)
. (3. 16)
Последнее выражение называется функцией распределения Бозе-Эйнштейна, которая описывает распределение бозонов по энергиям.
Если учесть спин, то надо умножить свободную энергию на число спиновых состояний s. Сумму (3. 15) можно найти, если заменить её интегралом по фазовому объёму и заменить дискретный спектр непрерывным 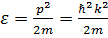 . Заметим, что теперь индекс
. Заметим, что теперь индекс  можно заменить индексом p или k. Тогда, с учетом (3. 10),
можно заменить индексом p или k. Тогда, с учетом (3. 10),
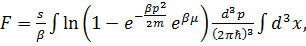 (3. 17)
(3. 17)
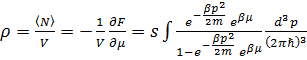 . (3. 18)
. (3. 18)
Введем обозначения: 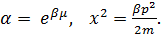 Тогда
Тогда
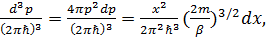 и
и
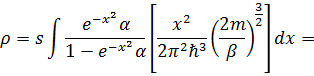
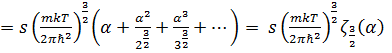 (3. 19)
(3. 19)
Мы ввели здесь дзета-функцию  . Задав
. Задав 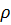 , можно найти
, можно найти  , а затем и
, а затем и 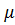 .
.
Для полной энергии (3. 12) получаем
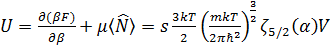 . (3. 20)
. (3. 20)
Рассмотрим случай малых плотностей или высоких температур, когда
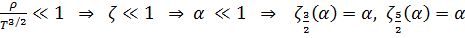 . В этом классическом предельном случае
. В этом классическом предельном случае 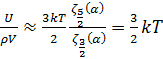 .
.
Конденсация Бозе - Эйнштейна.
Особый интерес представляет собой случай низких температур. При понижении температуры параметр  неограниченно возрастает, а дзета-функция при
неограниченно возрастает, а дзета-функция при 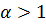 расходится. Температура, при которой
расходится. Температура, при которой 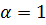 называется критической температурой Tc конденсации Бозе - Эйнштейна. Известно, что
называется критической температурой Tc конденсации Бозе - Эйнштейна. Известно, что  , и из (3. 19) находим
, и из (3. 19) находим
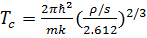 . (3. 21)
. (3. 21)
|
|
|
Вблизи этой температуры заменять суммирование (3. 15) интегрированием нельзя, так как низшие дискретны уровни вносят заметный вклад в сумму.
Рассмотрим 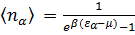 . Так как
. Так как 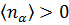 , то должно выполняться условие
, то должно выполняться условие 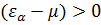 .
.
Пусть 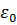 - основное невырожденное состояние, тогда
- основное невырожденное состояние, тогда
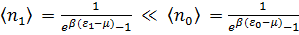 .
.
Если теперь взять 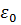 за начало отсчета энергии (
за начало отсчета энергии ( 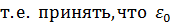 =0), то
=0), то 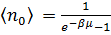 .
.
Отсюда следует, что 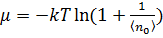 , а для больших
, а для больших 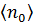
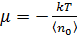 .
.
При низких температурах T химический потенциал  должен лежать вблизи нуля, поэтому для всех энергий
должен лежать вблизи нуля, поэтому для всех энергий 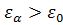 им можно пренебречь.
им можно пренебречь.
Тогда для T < Tc:
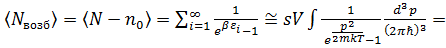
 , (3. 22)
, (3. 22)
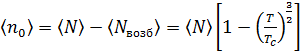 , (3. 23)
, (3. 23)
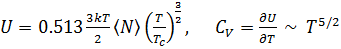 . (3. 24)
. (3. 24)
Для T > Tc внутренняя энергия имеет вид 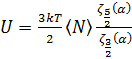 . Эта функция убывает с ростом температуры. Вблизи критической температуры теплоёмкость имеет острый излом (“cusp”).
. Эта функция убывает с ростом температуры. Вблизи критической температуры теплоёмкость имеет острый излом (“cusp”).
§3. 3. Идеальный газ Ферми - Дирака.
Для идеального газа фермионов (электронов) свободная энергия также определяется формулой (3. 15), в которой числа заполнения 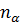 могут принимать всего два значения
могут принимать всего два значения 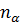 = 0, 1. Поэтому
= 0, 1. Поэтому
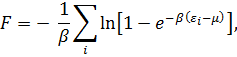
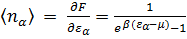 . (3. 25)
. (3. 25)
Последнее выражение называется функцией распределения Ферми-Дирака, которая описывает распределение фермионов по энергиям. Для вычисления свободной энергии снова перейдем от суммирования к интегрированию и учтём, что для электронов s=2:
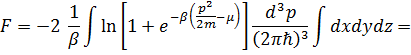
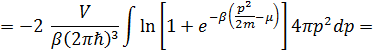
 , (3. 26)
, (3. 26)
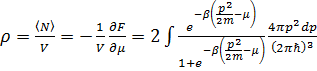 . (3. 27)
. (3. 27)
Рассмотрим некоторые свойства функции распределения Ферми-Дирака.
Рис. 3. 1. Заполнение состояний идеального ферми-газа при Т = 0 и при Т > 0.
Из (3. 25) следует, что при Т = 0 все состояния с энергиями  заполнены, а состояния с большими энергиями
заполнены, а состояния с большими энергиями  свободны.
свободны.
Так как свободные электроны занимают в импульсном пространстве сферу радиуса p0, то
 (3. 28)
(3. 28)
Величина
 (3. 29)
(3. 29)
|
|
|
называется энергией (уровнем) Ферми, а 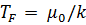 –температурой Ферми. Для простых металлов эту температуру можно оценить, используя две последние формулы -
–температурой Ферми. Для простых металлов эту температуру можно оценить, используя две последние формулы -  . Оказалось, что, например, для меди (и других металлов в твердом состоянии)
. Оказалось, что, например, для меди (и других металлов в твердом состоянии) 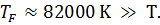 Говорят, что мы имеем сильно вырожденный электронный газ.
Говорят, что мы имеем сильно вырожденный электронный газ.
Найдем теперь плотность электронных состояний 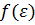 , т. е. число состояний с энергией
, т. е. число состояний с энергией 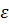 в интервале
в интервале 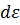 . Этому интервалу в импульсном пространстве отвечает сферический слой толщиной dp. Полное число состояний в данном слое
. Этому интервалу в импульсном пространстве отвечает сферический слой толщиной dp. Полное число состояний в данном слое 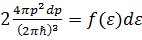 . Отсюда для квадратичного закона дисперсии
. Отсюда для квадратичного закона дисперсии 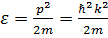 получаем
получаем
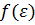 =
= 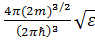 . (3. 30)
. (3. 30)
Полная энергия на единицу объёма при T=0 определяется выражением
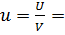
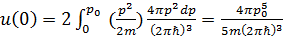 , а средняя энергия электрона в металле равна
, а средняя энергия электрона в металле равна
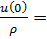
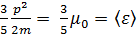 . (3. 31)
. (3. 31)
Для Т ≠ 0 функцияраспределения расплывается (см. Рис. 3. 1. ), а плотность и внутреннюю энергию можно вычислить лишь приближенно. Энергетический интервал расплывания функции распределения порядка kT, что много меньше значения уровня Ферми 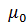 . В результате для низких температур имеем:
. В результате для низких температур имеем:

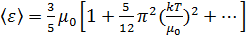 ,
,
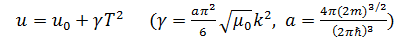 . (3. 32)
. (3. 32)
Отсюда следует линейная зависимость удельной теплоемкости металлов от температуры 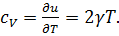
|
|
|


