 |
спиновым состояниям. . Операторы поляризации.
|
|
|
|
спиновым состояниям.
Операторы поляризации.
Вернемся к рассмотрению волновой функции электрона, движущегося в постоянном и однородном магнитном поле. В целях детального исследования поведения спина частицы в условиях синхротронного излучения оказалось целесообразным провести разделение решений уравнения Дирака по спиновым состояниям.
Как уже отмечалось, наряду с операторами 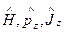 для определения спиновых состояний необходим четвертый оператор, коммутирующий с гамильтонианом, — оператор поляризации. В качестве такого оператора рассмотрим так называемый трехмерный вектор — оператор спина, который для свободной частицы имеет вид
для определения спиновых состояний необходим четвертый оператор, коммутирующий с гамильтонианом, — оператор поляризации. В качестве такого оператора рассмотрим так называемый трехмерный вектор — оператор спина, который для свободной частицы имеет вид
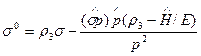 (8)
(8)
Этот оператор, впервые введенный Штехом, является единичным: его проекция на любое направление в пространстве 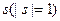 удовлетворяет требованию
удовлетворяет требованию
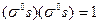
Как видно из(), в системе покоя частицы трехмерный вектор спина 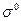 равен
равен 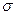 в направлении движения частицы (продольная поляризация). Поскольку, таким образом,
в направлении движения частицы (продольная поляризация). Поскольку, таким образом, 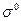 является унитарным преобразованием обычного оператора спина, собственные значения
является унитарным преобразованием обычного оператора спина, собственные значения 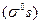 совпадают с собственными значениями оператора спина в системе покоя. Поэтому волновая функция преобразуется из системы покоя в лабораторную систему с помощью преобразований Лоренца безотносительно к состояниям поляризации: поляризация остается неизменной во всех системах отсчета.
совпадают с собственными значениями оператора спина в системе покоя. Поэтому волновая функция преобразуется из системы покоя в лабораторную систему с помощью преобразований Лоренца безотносительно к состояниям поляризации: поляризация остается неизменной во всех системах отсчета.
Заметим далее, что на решениях уравнения Дирака 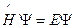 вид оператора
вид оператора 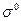 может быть несколько изменен: с помощью получим выражение
может быть несколько изменен: с помощью получим выражение
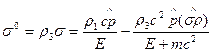
которое допускает простое обобщение на случай движения частицы в магнитном поле.
|
|
|
Действительно, заменяя в соответствии с общими правилами
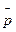 на кинетический импульс
на кинетический импульс 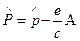 , получаем
, получаем
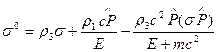
Однако теперь при движении электрона в магнитном поле в отличие от движения свободной частицы в общем случае 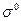 не коммутирует с гамильтонианом. Но тем не менее можно найти интеграл движения: сохраняется проекция
не коммутирует с гамильтонианом. Но тем не менее можно найти интеграл движения: сохраняется проекция 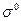 на направление движения электрона (продольная поляризация)
на направление движения электрона (продольная поляризация) 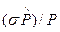 и проекция
и проекция 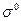 на направление магнитного поля
на направление магнитного поля
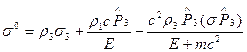
Выбирая теперь 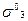 в качестве оператора поляризации (поперечная поляризация) и подчиняя волновую функцию
в качестве оператора поляризации (поперечная поляризация) и подчиняя волновую функцию 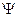 требованию быть собственной для этого оператора
требованию быть собственной для этого оператора
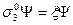 (7)
(7)
где С= —1 соответствует ориентации спина электрона соответственно вдоль и против магнитного поля, получаем возможность определения всех необходимых чисел, характеризующих состояние: п — главного квантового числа (энергии электрона); 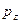 — импульса электрона вдоль поля;
— импульса электрона вдоль поля; 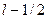 — проекции полного момента на направление поля;
— проекции полного момента на направление поля; 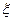 -спина. Спиновые коэффициенты определяются из (6) и имеют вид
-спина. Спиновые коэффициенты определяются из (6) и имеют вид
 (8)
(8)
Как видно, при переходе в систему покоя решения (8) переходят в паулиевские волновые функции 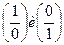 , которые соответствуют двум альтернативным ориентациям спина по отношению к внешнему магнитному полю. Такой подход (без введения оператора поляризации) развивался одним из нас в ранних исследованиях спиновых эффектов.
, которые соответствуют двум альтернативным ориентациям спина по отношению к внешнему магнитному полю. Такой подход (без введения оператора поляризации) развивался одним из нас в ранних исследованиях спиновых эффектов.
Остановимся далее на вопросе о введении в теорию СИ ковариантных операторов поляризации. Вопрос прежде всего заключается в том, что введение оператора 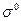 для описания спиновых свойств электрона не является единственной возможностью. Более того, сам оператор
для описания спиновых свойств электрона не является единственной возможностью. Более того, сам оператор 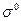 вызывает известное чувство неудовлетворенности — он является нековариантным и преобразуется при переходе к новой лоренцевой системе координат по особым правилам.
вызывает известное чувство неудовлетворенности — он является нековариантным и преобразуется при переходе к новой лоренцевой системе координат по особым правилам.
Следует заметить, что наиболее просто и естественно спиновые свойства электрона могут быть описаны в случае нерелятивистского движения. Тогда в соответствии с теорией Паули спин частицы определяется совершенно независимо от ее орбитального движения с помощью оператора 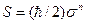 , содержащего двухрядные матрицы Паули
, содержащего двухрядные матрицы Паули 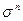 , собственные значения которых ±1. Именно это обстоятельство и лежало, по-видимому, в основе предложения Дарвина определять поляризацию свободного электрона как ожидаемые значения спинового оператора, а в лоренцевой системе координат, в которой электрон покоится.
, собственные значения которых ±1. Именно это обстоятельство и лежало, по-видимому, в основе предложения Дарвина определять поляризацию свободного электрона как ожидаемые значения спинового оператора, а в лоренцевой системе координат, в которой электрон покоится.
|
|
|
Вопрос об определении спина в релятивистской теории Дирака становится более сложным: сохраняется, как известно, только полный момент количества движения

и в силу этого, вообще говоря, спиновые и орбитальные свойства движения частиц выступают как неразрывное целое. Поэтому задача описания спиновых свойств электрона в случае его релятивистского движения становится связанной с возможностью инвариантного отделения спина от полного момента количества движения. Мы вернемся еще к этому вопросу, но прежде рассмотрим ковариантные операторы поляризации.
Ковариантная формулировка теории в известной мере вносит сложности в физическую интерпретацию операторов. Для достижения большей ясности в этом вопросе удобно рассмотреть унитарное преобразование Фолди — Ваутхайзена (ФВ-преобразование), которое переводит волновую функцию свободной частицы из лабораторной системы в систему покоя, вследствие чего функция становится двухкомпонентной:
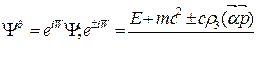
Так как при унитарном преобразовании операторов
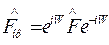
их средние значения не меняются, то для перевода самих операторов в систему покоя преобразование Фолди — Ваутхайзена следует дополнить соответствующим операторным преобразованием Лоренца
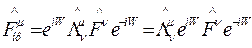
где матрица преобразования для случая движения системы координат вдоль оси 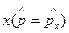 имеет обычный вид преобразований Лоренца. В дальнейшем нам потребуется обратное преобразование, которое реализуется с помощью матрицы
имеет обычный вид преобразований Лоренца. В дальнейшем нам потребуется обратное преобразование, которое реализуется с помощью матрицы
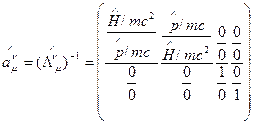 (9)
(9)
элементы которой" приведены в явном виде,.
Воспользуемся далее обратным преобразованием операторов из системы покоя 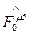 в лабораторную систему координат, тогда
в лабораторную систему координат, тогда
 (10)
(10)
Прежде чем перейти к рассмотрению ковариантных операторов поляризации, заметим, что в релятивистской теории Дирака интерпретация операторов затрудняется (как это отмечалось еще Дираком) ввиду сложного характера движения релятивистской частицы. Электрон Дирака совершает особое «дрожащее движение» (zitterbewegung), характеризуемое наряду с поступательным движением быстрыми осцилляциями с частотой 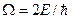 . Подобный сложный характер движения обусловлен особым процессом интерференции состояний, соответствующих различным знакам (±Е), поскольку уравнение Дирака описывает зарядово-сопряженные состояния частицы с энергией
. Подобный сложный характер движения обусловлен особым процессом интерференции состояний, соответствующих различным знакам (±Е), поскольку уравнение Дирака описывает зарядово-сопряженные состояния частицы с энергией  . Преобразование Фолди — Ваутхайзена, приводящее волновую функцию к двухкомпонентному виду, устраняет трудности с «дрожащим движением», поскольку операторы в ФВ-представлении не смешивают между собою зарядово-сопряженные состояния. Подобный подход (справедливый только для свободных частиц) снимает многие трудности, связанные с физической интерпретацией операторов.
. Преобразование Фолди — Ваутхайзена, приводящее волновую функцию к двухкомпонентному виду, устраняет трудности с «дрожащим движением», поскольку операторы в ФВ-представлении не смешивают между собою зарядово-сопряженные состояния. Подобный подход (справедливый только для свободных частиц) снимает многие трудности, связанные с физической интерпретацией операторов.
|
|
|
Рассмотрим прежде всего уже известный нам оператор рз0 с точки зрения унитарного ФВ-преобразования. Выбирая в качестве исходного оператора в системе покоя электрона
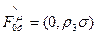 (10)
(10)
получаем уже известный трехмерный единичный оператор спина
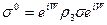
и, подвергая его преобразованиям Лоренца в соответствии с(8), (9), получаем релятивистское ковариантное обобщение в лабораторной системе координат в виде четырехмерного псевдовектора спина Баргмана — Вигнера
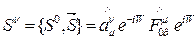 (11)
(11)
где
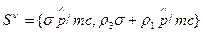 (12)
(12)
К такому же выражению можно прийти в результате преобразования (11) для 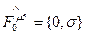 (мы привели все величины к безразмерному виду). Такое ковариантное обобщение
(мы привели все величины к безразмерному виду). Такое ковариантное обобщение 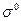 не является единственно возможным. Требование (9) преобразования
не является единственно возможным. Требование (9) преобразования 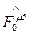 по закону трансформации 4-вектора может быть заменено преобразованием по закону тензора второго ранга. Тогда, полагая
по закону трансформации 4-вектора может быть заменено преобразованием по закону тензора второго ранга. Тогда, полагая
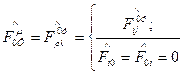
где 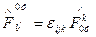 ;
; 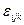 — известный символ Леви — Чивита, приходим к тензору поляризации — антисимметричному тензору второго ранга
— известный символ Леви — Чивита, приходим к тензору поляризации — антисимметричному тензору второго ранга
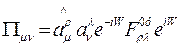
где отличные от нуля компоненты имеют вид
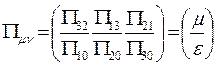
При этом компоненты операторов магнитной 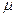 и электрической
и электрической  поляризаций равны
поляризаций равны
|
|
|
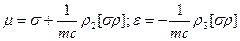 (13)
(13)
(отдельные компоненты операторов 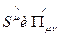 можно найти в ранних работах А. А. Соколова. )
можно найти в ранних работах А. А. Соколова. )
Таким образом, псевдовектор спина (12) и тензор-оператор поляризации (13) являются инвариантным обобщением единичного вектора спина 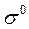 и получаются путем его преобразования из системы покоя в лабораторную систему. Отсюда следует, что все три способа описания спина свободного электрона:
и получаются путем его преобразования из системы покоя в лабораторную систему. Отсюда следует, что все три способа описания спина свободного электрона: 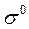 ,
, 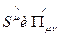 полностью эквивалентны.
полностью эквивалентны.
В случае движения частицы во внешнем электромагнитном поле операторы 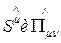 допускают простое обобщение, которое достигается обычной заменой
допускают простое обобщение, которое достигается обычной заменой 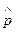 на оператор кинетического импульса
на оператор кинетического импульса 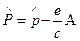 , где А — вектор-потенциал внешнего поля. Вопрос об интегралах движения должен быть рассмотрен конкретно для данной задачи. Так, в частности, в задаче о движении электрона в однородном магнитном поле в качестве оператора поляризации, позволяющего разделить решения уравнения Дирака по спиновым состояниям, наряду с
, где А — вектор-потенциал внешнего поля. Вопрос об интегралах движения должен быть рассмотрен конкретно для данной задачи. Так, в частности, в задаче о движении электрона в однородном магнитном поле в качестве оператора поляризации, позволяющего разделить решения уравнения Дирака по спиновым состояниям, наряду с 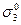 можно выбрать также коммутирующие с гамильтонианом проекции
можно выбрать также коммутирующие с гамильтонианом проекции
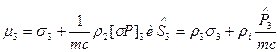
являющиеся интегралами движения. Заметим, что оператор 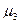 сохраняет свойства интеграла движения и при учете аномального момента электрона.
сохраняет свойства интеграла движения и при учете аномального момента электрона.
Все эти операторы обладают ковариантными свойствами и в нерелятивистском приближении автоматически переходят в матрицы Паули, допуская тем самым простую физическую интерпретацию.
Наряду с рассмотренными операторами поляризации можно ввести также инварианты 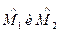 с помощью которых поляризационные состояния электронов в магнитном поле можно определить в качестве собственных значений этих операторов:
с помощью которых поляризационные состояния электронов в магнитном поле можно определить в качестве собственных значений этих операторов:
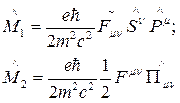 (14)
(14)
которые в случае однородного магнитного поля имеют вид
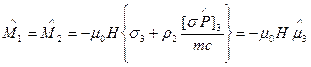
Здесь 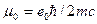 — магнетон Бора, a
— магнетон Бора, a 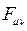 и
и 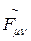 — соответственно тензор электромагнитного поля и дуальная к нему величина,
— соответственно тензор электромагнитного поля и дуальная к нему величина, 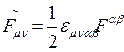 . Как видно из (14), оба инварианта выражаются через оператор
. Как видно из (14), оба инварианта выражаются через оператор 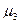 . Инвариант
. Инвариант 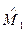 был впервые введен в теорию СИ в1967, с нашей точки зрения, метод инвариантов наиболее предпочтителен при описании Спиновых свойств частиц
был впервые введен в теорию СИ в1967, с нашей точки зрения, метод инвариантов наиболее предпочтителен при описании Спиновых свойств частиц
Мы уделили особое внимание вопросам описания спиновых свойств электрона при его движении в магнитном поле. На первый взгляд это кажется не совсем оправданным, однако принципиальные вопросы возможности измерения спина релятивистских частиц требуют с нашей точки зрения глубокого анализа.
Вернемся теперь к полному моменту количества движения 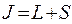 и рассмотрим оператор координаты г в ФВ-представлении. Пусть в системе покоя
и рассмотрим оператор координаты г в ФВ-представлении. Пусть в системе покоя 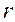 — суть координата в теории Дирака
— суть координата в теории Дирака 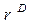 . Тогда унитарное ФВ-преобразование дает в лабораторной системе
. Тогда унитарное ФВ-преобразование дает в лабораторной системе
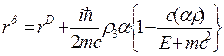
В случае отсутствия движения (  ) мы приходим к так называемому оператору «центра инерции», впервые встречающемуся у В. А. Фока. Физически с помощью ФВ-преобразования устраняется дрожание координаты, и теперь оператор координаты центра инерции показывает, что электрон как бы размазывается в области пространства, радиус которой имеет порядок комптоновской длины волны, — так называемый квантовый радиус электрона. Если теперь в выражении для орбитального момента произвести замену радиуса-вектора
) мы приходим к так называемому оператору «центра инерции», впервые встречающемуся у В. А. Фока. Физически с помощью ФВ-преобразования устраняется дрожание координаты, и теперь оператор координаты центра инерции показывает, что электрон как бы размазывается в области пространства, радиус которой имеет порядок комптоновской длины волны, — так называемый квантовый радиус электрона. Если теперь в выражении для орбитального момента произвести замену радиуса-вектора 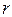 оператором центра инерции
оператором центра инерции 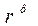 , то получим, что полный момент количества движения равен
, то получим, что полный момент количества движения равен
|
|
|
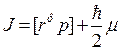
Важно подчеркнуть, что теперь в этом выражении сохраняется каждый из моментов (орбитальный и спиновый) в отдельности.
Таким образом, мы приходим к доказательству принципиальной возможности наблюдения спиновых свойств частиц в релятивистском движении независимо от орбитального движения.
И в заключение отметим, что наряду с ФВ-преобразованием предингеровское дрожание может быть устранено на пути выделения так называемой четной части операторов. Переход к дефинитной четности операторов открывает возможности их наглядной интерпретации при соблюдении необходимых требований ковариантности. Выделение четной части операторов не смешивающей состояния, принадлежащие различному знаку энергии, достигается введением знакового оператора
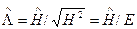
(мы ограничиваемся рассмотрением чисто магнитного поля). Тогда четная часть оператора 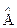 имеет вид
имеет вид
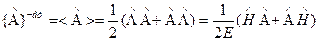 (15)
(15)
если ограничиться только положительными значениями энергии. Такой подход возможен в одночастичном варианте теории, когда напряженность внешнего поля далека от критических значений. В этих ограничениях с помощью антикоммутатора (14) можно показать, что
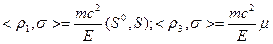
т. е. на этом пути мы снова приходим к операторам 4-псевдовектора спина 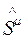 и тензора поляризации
и тензора поляризации  .
.
Приведем теперь матрицу спиновых коэффициентов 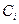 для разделения решений уравнения Дирака с помощью оператора поляризации
для разделения решений уравнения Дирака с помощью оператора поляризации 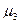 , связанного с инвариантом
, связанного с инвариантом 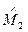 :
:
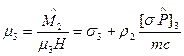
Наложив на волновую функцию 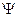 требование быть собственной функцией этого оператора
требование быть собственной функцией этого оператора
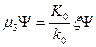
получим систему уравнений
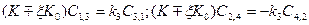 (15)
(15)
которая имеет нетривиальные решения при 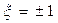 . Это соответствует двум возможным спиновым состояниям электрона: проекции спина вдоль магнитного поля (
. Это соответствует двум возможным спиновым состояниям электрона: проекции спина вдоль магнитного поля ( 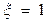 ) и против поля (
) и против поля (  ). Совместное решение (15) и (1) приводит к результату
). Совместное решение (15) и (1) приводит к результату
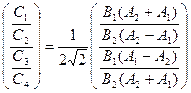
где
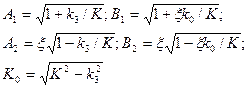
Таким образом, закончено определение полного набора, необходимого для описания квантовых состояний электрона в постоянном и однородном магнитном поле. Можно лишь в заключение отметить, что для описания состояний поляризации по отношению к направлению магнитного поля оба оператора (  ) в известной степени эквивалентны. Это вытекает из следующей, имеющей место связи между ними:
) в известной степени эквивалентны. Это вытекает из следующей, имеющей место связи между ними:
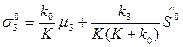
При отсутствии движения частицы вдоль направления магнитного поля (  ) эти операторы совпадают, и поэтому их применение полностью равносильно. Однако при учете отдачи при излучении фотонов электроном может измениться составляющая импульса частицы вдоль поля, поэтому влияние квантовых флуктуации на спиновые состояния, собственные для операторов
) эти операторы совпадают, и поэтому их применение полностью равносильно. Однако при учете отдачи при излучении фотонов электроном может измениться составляющая импульса частицы вдоль поля, поэтому влияние квантовых флуктуации на спиновые состояния, собственные для операторов  , может оказаться различным.
, может оказаться различным.
В связи с этим надо заметить, что для разделения состояний электрона по спиновым состояниям нам представляется более предпочтительным оператор 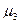 , обладающий ковариантными свойствами, он непосредственно связан с инвариантами
, обладающий ковариантными свойствами, он непосредственно связан с инвариантами 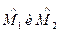 , хотя в главных чертах описание закономерностей в квантовых эффектах можно провести и с помощью
, хотя в главных чертах описание закономерностей в квантовых эффектах можно провести и с помощью 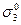 .
.
Учет взаимодействия электрона с электромагнитным полем излучения, строго говоря, приводит к смешанным состояниям, и это требует для описания спиновых свойств частицы введения матрицы плотности. Этого вопроса мы коснемся позже.
|
|
|


