 |
Атаки типа «Отказ в обслуживании»
|
|
|
|
Атаки типа «Отказ в обслуживании»
• выявление версий ОС и сетевых приложений, подверженных таким атакам
Результат тестирования – экспертное заключение
(Акт проверки защищенности АИС от НСД)
74. реальное состояние защищенности АИС от внутренних и внешних угроз,
75. перечень найденных изъянов в настройках систем безопасности
76. рекомендации по повышению степени защищенности АИС
Анализ информационных рисков организации
77. определение, что именно подлежит защите
78. построение перечня угроз
79. анализ способов защиты
80. определение вероятности угроз оценка ущерба в случае реализации атак
Математические основы криптографии
Пусть задано некоторое (конечное или бесконечное) множество G, на котором определена операция умножения, т. е. определен закон, сопоставляющий любой паре a, b элементов из G некий элемент из G называемый произведением а и b и обозначаемый Символом а ∙ b. Предположим, что эта операция умножения удовлетворяет следующим условиям:
I. Условие ассоциативности. Для любых трех элементов a, b, c множества G справедливо соотношение:
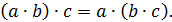
Это значит следующее. Обозначим через d элемент множества G, являющийся произведением элементов a и b\ точно так же обозначим через е элемент b ∙ c множества G. Тогда d∙ c и a∙ e являются одним и тем же элементом множества G.
II. Условие существования нейтрального элемента. Среди элементов множества G имеется некоторый определенный элемент, называемый нейтральным элементом и обозначаемый символом 1, такой, что
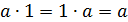
III. Условие существования обратного элемента к каждому данному элементу. К каждому данному элементу a множества G можно подобрать такой элемент b того же множества G, что
|
|
|
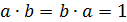
Элемент b называется обратным к элементу a и обозначается а-1.
Множество G с определенной в нем операцией умножения, удовлетворяющей только что перечисленным трем условиям, называется группой; сами эти условия называются аксиомами группы.
Операция умножения, удовлетворяющая аксиомам группы, иногда называется групповой операцией
Пусть в группе G, кроме указанных выше трех аксиом, оказывается выполненным еще и следующее условие:
IV. Условие коммутативности:
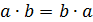
В этом случае группа G называется коммутативной или абелевой группой.
Группа называется конечной, если она состоит из конечного числа элементов; в противном случае она называется бесконечной.
Число элементов конечной группы называется ее порядком.
1) с группой целых чисел (групповая операция - обычное сложение целых чисел);
2) с группой отличных от нуля рациональных чисел (групповая операция - обычное умножение рациональных чисел);
3) с группой поворотов правильного треугольника (групповая операция-композиция поворотов);
4) с клейновской группой порядка 4 (групповая операция-умножение букв a0, a1, a2, a3, задаваемое таблицей 2);
5) с группой поворотов правильного четырехугольника (групповая операция- композиция поворотов);
6) с группой поворотов правильного «-угольника.
Все эти группы коммутативны. Группа целых чисел и группа ненулевых рациональных чисел бесконечны; остальные - конечные группы.
Порядок элемента обозначается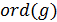 
. Заметим, что 
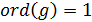тогда и только тогда, когда 
.
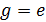Следующее предложение объясняет, почему для порядка группы и порядка элемента используется одно и то же слово.
Предложение Пусть G - группа и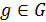 
. Тогда 
.
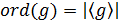Доказательство. Заметим, что если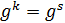 
, то 
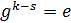. Поэтому если элемент g имеет бесконечный порядок, то все элементы 
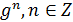, попарно различны, и подгруппа 
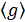содержит бесконечно много элементов. Если же порядок элемента д равен т. то из минимальности числа т следует, что элементы 
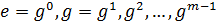попарно различны. Далее, для всякого 
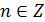мы имеем 
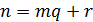, где 
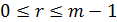, и
|
|
|
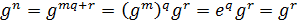
Следовательно,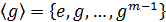 
и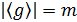 
Определение Группа G называется циклической, если найдётся такой элемент 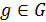, что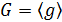 
.
Ясно, что любая циклическая группа коммутативна и не более чем счётна. Примерами циклических групп являются группы (Z, +) и (Zn, +), n≥ 1.
Перейдем ещё к одному сюжету, связанному с парой группа-подгруппа.
Определение 11. Пусть G - группа,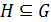 
- подгруппа и 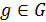. Левым смежным классом элемента g группы G по подгруппе Н называется подмножество
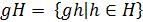
Лемма 1. Пусть G - группа, 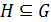- её подгруппа и 
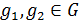. Тогда либо 
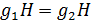, либо 
.
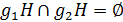Доказательство. Предположим, что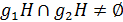 
, т. е. 
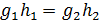Для некоторых 
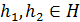. Нужно доказать, что 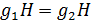. Заметим, что 
. Обратное включение доказывается аналогично.
Лемма 2. Пусть G - группа и 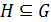конечная подгруппа. Тогда 
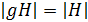для любого .
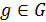Доказательство. Поскольку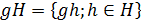 
. в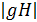 
элементов не больше, чем в Н. Если 
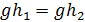, то домножаем слева на g-1 и получаем h1 = h2. Значит, все элементы вида gh. где 
, попарно различны, откуда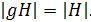 
Определение Пусть G - группа и 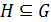подгруппа. Индексам подгруппы H в группе G называется число левых смежных классов G по H.
Индекс группы G по подгруппе Я обозначается [G: H].
Теорема Лагранжа. Пусть G конечная группа и 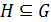подгруппа. Тогда
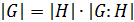
Доказательство. Каждый элемент группы G лежит в (своём) левом смежном классе по подгруппе H. разные смежные классы не пересекаются (лемма 1) и каждый из них содержит по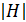 
элементов (лемма 2).
Следствие 1. Пусть G - конечная группа и 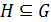- подгруппа. Тогда 
делит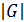 
.
Следствие 2. Пусть G - конечная группа и 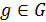. Тогда ord(g) делит .
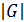Доказательство. Это вытекает из следствия 1 и предложения 2.
Следствие 3. Пусть G - конечная группа и 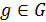. Тогда 
.
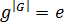Доказательство. Согласно следствию 2, мы имеем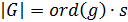 
. откуда 
.
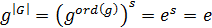Следствие 4 (Малая теорема Ферма). Пусть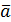 
- ненулевой вычет по простому модулю р. Тогда
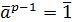
Доказательство. Вытекает из следствия 3, применённого к группе (Zp\{0}, х).
Следствие 5. Пусть G - группа. Предположим, что |G| - простое число. Тогда G - циклическая группа, порождаемая любым своим неединичным элементом.
Доказательство. Пусть 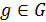- произвольный неединичный элемент. Тогда циклическая подгруппа 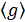содержит более одного элемента и 
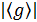делит |G| но следствию 1. Значит, 
, откуда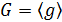
|
|
|
Наряду с левым смежным классом можно определить правый смежный класс элемента д группы G но подгруппе H:
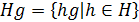
Повторяя доказательство теоремы Лагранжа для правых смежных классов, мы получим, что для конечной группы G число правых смежных классов по подгруппе Н равно числу левых смежных классов и равно 
. В то же время равенство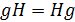 
выполнено не всегда. Разумеется, оно выполнено, если группа G абелева. Подгруппы H (неабелевых) групп G\ для которых 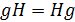выполнено для любого 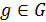. будут изучаться в следующей лекции.
|
|
|
