 |
Равносильное определение кратности корня.
|
|
|
|
Алгебраические многочлены. Разложение многочленов на множители.
Определение. Алгебраическим многочленом n-й степени (nÎN) называется выражение вида: Pn(z)=c0zn+c1zn-1+…+cn-1z+cn (1)
где z=x+iy, c0,c1,…,cn-1,cn – постоянные комплексные числа (c0≠0).
Алгебраическим многочленом нулевой степени называется любая комплексная постоянная.
Пусть Pn(z) и Fm(z) (deg P=n, deg F=m) - алгебраические многочлены, причем m£n, тогда имеет место равенство:
Pn(z)=Fm(z)×Q(z)+R(z) (2)
где Q(z) и R(z) – некоторые алгебраические многочлены, причем
deg Q(z)=deg Pn(z)-deg Fm(z)=n-m, deg R(z)<deg Fm(z).
Операция по нахождению алгебраических многочленов Q(z) и R(z) по заданным многочленам Pn(z) и Fm(z) называется делением многочлена Pn(z) на Fm(z). Pn(z) - делимое, Fm(z) – делитель, Q(z) – частное, R(z) – остаток от деления Pn(z) на Fm(z).
(Производится при помощи алгоритма Евклида)
(Любой алгебраический многочлен делится на отличный от нуля многочлен нулевой степени).
Определение. Комплексное число а называется корнем алгебраического многочлена Pn(z), если Pn(а)=0 (3)
Теорема 1. Алгебраический многочлен Pn(z) ненулевой степени делится без остатка на двучлен (z-a) без остатка лишь тогда, когда а является корнем Pn(z).
Доказательство. Для Pn(z) и F1(z)=z-a запишем соотношение (2):
Pn(z)=(z-а)×Q(z)+R(z) (4)
Т.к. deg R(z)<deg (z-а)=1, то R(z) – алгебраический многочлен нулевой степени, т.е. R(z)=const=C.
Тогда соотношение (4) примет вид: Pn(z)=(z-а)×Q(z)+С (5)
Положив в (5) z=a, получим Pn(а)=(а-а)×Q(а)+С, т.е. Pn(а)=С.
Т.о. Pn(z) делится без остатка на (z-а) лишь тогда, когда Pn(а)=0, т.е. когда а является корнем многочлена Pn(z). Ч.т.д.
Теорема 2. Пусть имеется алгебраический многочлен
Pn(z)=c0zn+c1zn-1+…+cn-1z+cn
Если Pn(z)º0, то c0=c1=…=cn-1=cn=0.
Доказательство. По условию Pn(z)º0, т.е. c0zn+c1zn-1+…+cn-1z+cnº0 (6)
Т.к. левая часть (6) равна нулю "z, то положим в (6) z=0, получим cn=0. Тождество (6) может быть переписано в виде: z(c0zn-1+c1zn-2+…+cn-1)º0 (7)
|
|
|
Тождество (7) имеет место лишь тогда, когда
c0zn-1+c1zn-2+…+cn-1º0 (8)
Положив в (8) z=0, получим cn-1=0.
Проводя аналогичные рассуждения, получим cn-2=0, cn-3=0,…, c1=0, c0=0. ч.т.д.
Теорема 3. Пусть имеются алгебраических многочлена степени n:
Pn(z)=c0zn+c1zn-1+…+cn-1z+cn и P*n(z)=c*0zn+c*1zn-1+…+c*n-1z+c*n.
Если Pn(z)ºP*n(z), то c0=c*0, c1=c*1…cn-1=c*n-1,cn=c*n.
Доказательство. По условию Pn(z)ºP*n(z)ÛPn(z)-P*n(z)º0Û
Û(c0-c*0)zn+(c1-c*1)zn-1+…+(cn-1-c*n-1)z+(cn-c*n)º0.
В силу теоремы 2, последние тождество имеет место лишь тогда, когда
Ûc0-c*0=0, c1-c*1=0,…cn-1-c*n-1=0, cn-c*n=0, т.е. когда
(c0-c*0)zn+(c1-c*1)zn-1+…+(cn-1-c*n-1)z+(cn-c*n)º0 ч.т.д.
Основная теорема алгебры. Всякий алгебраический многочлен Pn(z) ненулевой степени (n³1) имеет хотя бы один корень.
Следствие. Алгебраический многочлен Pn(z) степени n³1 имеет ровно n корней.
Доказательство (?). По условию, Pn(z) - алгебраический многочлен степени n³1. По основной теореме алгебры он имеет хотя бы один корень. Обозначим этот корень через а1. Тогда Pn(z) можно представить в виде:
Pn(z)=(z-a1)Pn-1(z) (9)
Где Pn-1(z) - алгебраический многочлен степени (n-1).
Если n-1¹0, т.е. если n>1, то Pn-1(z) - алгебраический многочлен ненулевой степени, и, следовательно, по основной теореме алгебры он имеет хотя бы один корень. Обозначим этот корень через а2. Тогда Pn-1(z) можно представить в виде:
Pn-1(z)=(z-a2)Pn-2(z) (10)
Где Pn-2(z) - алгебраический многочлен степени (n-2).
Продолжая этот процесс аналогичным образом, на n-м шаге будем иметь:
P1(z)=(z-an)P0(z)
Где P0(z) - алгебраический многочлен нулевой степени, т.е. P0(z)=с.
Тогда P1(z)=(z-an)×с (11)
Учитывая (9), (10), (11), можно написать, что
Pn(z)=с(z-a1)(z-a2)…(z-an) (12) - разложение многочлена Pn(z) на множители. Причем, с=с0, a1,a2,…,an корни Pn(z).
Кратные корни алгебраического многочлена.
Среди корней a1,a2,…,an многочлена Pn(z) могут оказаться равные.
Пусть a,b,…,l различные корни Pn(z). Тогда для Pn(z) разложение (9) имеет вид:
|
|
|
Pn(z)=с0(z-a)a(z-b)b…(z-l)l (1)
где a,b,..,lÎN; a³1, b³1,…,l³1; a+b+…+l=n
Если для многочлена Pn(z) справедливо разложение (1), то число а является корнем Pn(z) кратности a, число b является корнем Pn(z) кратности b,…, число l является корнем Pn(z) кратности l.
Корень, кратность которого равна единице, называют простым корнем.
Равносильное определение кратности корня.
Число а называется корнем кратности a многочлена Pn(z), если для Pn(z) справедливо представление в виде:
Pn(z)=(z-a)aφ(z) (2)
где φ(а)¹0.
Теорема (признак кратности корня) (б.д.). Для того, чтобы число а было корнем кратности a многочлена Pn(z), необходимо и достаточно, чтобы
Pn(а)=0,  =0,…,
=0,…,  =0, но
=0, но 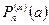 ¹0.
¹0.
Свойства многочленов с вещественными коэффициентами.
Рассмотрим алгебраический многочлен с вещественными коэффициентами:
Pn(х)=а0хn+а1хn-1+…+аn-1х+аn (1)
где а0,а1,…,аn-1,аn – постоянные вещественные числа (а0≠0).
Теорема (о комплексных корнях алгебраического многочлена с действительными коэффициентами). Если комплексное число а=a+ib (b¹0) является корнем Pn(х) кратности k, то сопряженное число  =a-ib тоже является корнем Pn(х), причем той же кратности k.
=a-ib тоже является корнем Pn(х), причем той же кратности k.
Следствие. Совокупность комплексных корней многочлена с вещественными коэффициентами распадается на пары взаимно сопряженных корней одной и той же кратности.
На комплексной плоскости корни многочлена с вещественными коэффициентами располагаются симметрично относительно вещественной оси. На самой вещественной оси располагаются вещественные корни. (Рисунок).
Пусть Pn(х) – алгебраический многочлен степени n>1 с вещественными коэффициентами.
Пусть a,b,…,с – вещественные корни многочлена Pn(х) кратностей a,b,…,g соответственно, а l и  ,…,m и
,…,m и 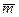 - сопряженных комплексных корней кратностей l,…,m соответственно. Тогда для Pn(х) справедливо разложение:
- сопряженных комплексных корней кратностей l,…,m соответственно. Тогда для Pn(х) справедливо разложение:
Pn(х)=а0(х-a)a(х-b)b…(х-с)g(х-l)l(х-  )l…(х-m)m(х-
)l…(х-m)m(х- 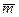 )m (2)
)m (2)
(Здесь a+b+…+g+2l+…+2m=n)
(х-l)l(х-  )l=(x2+px+q)l
)l=(x2+px+q)l
…..
(х-m)m(х- 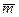 )m=(x2+rx+s)m
)m=(x2+rx+s)m
где(x2+px+q),…,(x2+rx+s) – квадратные трехчлены с вещественными коэффициентами. Поэтому разложение (4) для Pn(х) примет вид:
Pn(х)=а0(х-a)a(х-b)b…(х-с)g(x2+px+q)l…(x2+rx+s)m (5)
где все коэффициенты вещественны.
Замечание. Может случиться, что в разложении (5) линейные или квадратные сомножители отсутствуют. Это соответствует случаям, когда отсутствуют вещественные или, соответственно, комплексные корни у Pn(х).
|
|
|
|
|
|


