 |
Непосредственное интегрирование.
|
|
|
|
Глава 5. Неопределенный интеграл.
Раздел 5.1. Первообразная функции и неопределенный интеграл.
Основные понятия.
Одной из основных задач дифференциального исчисления является отыскание производной /дифференциала заданной функции.
Различные вопросы математики, естествознания, техники приводят к решению обратной задачи: восстановлению функции по известной ее производной (или известному дифференциалу).
Определение 1. Функция F(х) называется первообразной для функции f(х) на некотором промежутке, если в каждой точке этого промежутка
 .
.
Или, что то же

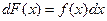 .
.
Пример:
1. 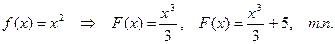 ;
;
 2.
2. 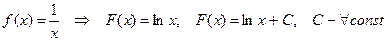 .
.
Определение 2. Семейство первообразных F(x)+C для f(x) на некотором промежутке называется неопределенным интегралом.
Основная задача интегрального исчисления: по данной функции f(х) отыскать все F(x).
Этот факт записывают:
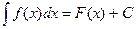 *),
*),
где
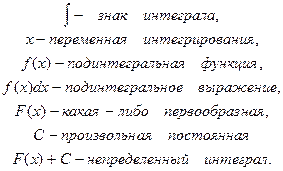
Процесс отыскания F(x) и F(x)+C называется интегрированием функции f(x), или, иногда, говорят “взять от f(х) интеграл”.
Заметим, что правильность интегрирования всегда можно проверить дифференцированием результата.
Для одной и той же функции f(х) первообразные могут внешне отличаться друг от друга.
 |
Пример:

 ; и
; и 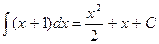 .
.
Легко убедиться, что производные от левых частей каждого равенства совпадают.
Кстати, потому интегрирование и неопределенное, что при этом не важно, какая из первообразных найдена.
5.1.2. Таблица неопределенных интегралов основных элементарных функций.
Эта таблица*) получается из определения неопределенного интеграла и таблицы дифференциалов основных элементарных функций.
1. 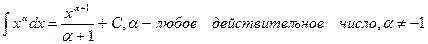 ,
,
2. 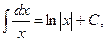
3. 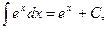
4. 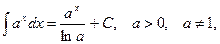
5. 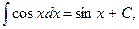
6. 
7. 
8. 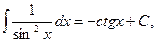
9. 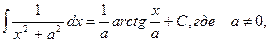
10. 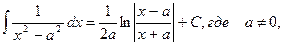
11. 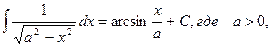
12. 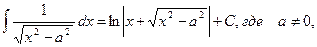
13. 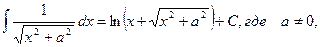
14. 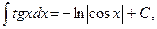
15. 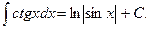
|
|
|
И ответим на вопрос: у всякой ли функции, существует первообразная, и если существует, то одна или их много?
Теорема. Для всякой непрерывной на данном промежутке функции существует первообразная.
В дальнейшем изложении, не обговаривая этого особо, функции, для которых ищутся первообразные, будем считать непрерывными на рассматриваемых промежутках, а конкретные элементарные функции будем рассматривать только на промежутках их непрерывности.
В связи с этим возникает вопрос о так называемых неберущихся (не интегрируемы в элементарных функциях; не интегрируемы в конечном виде) интегралах. Это (примеры):

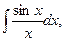
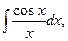

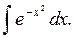
Следует различать существование неопределенного интеграла и возможность его выражения через элементарные функции. Указанные интегралы существуют, но средств – основных элементарных функций – оказывается недостаточно для того, чтобы составить из них конечные выражения для этих интегралов.
5.1.3.Свойства неопределенного интеграла.
1. 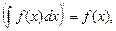
2. 
3. 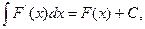
4. 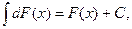
5. 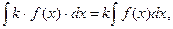
6. 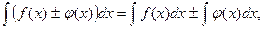
7.Инвариантность формул интегрирования:  , где
, где  - любая дифференцируемая функция от х.
- любая дифференцируемая функция от х.
Заметим, что при практическом интегрировании без этих свойств обойтись невозможно.
Практикум по разделу 5.1.
Задание 1. Найти:
а)  ; б)
; б) 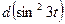 ; в)
; в) 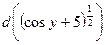 ;
;
г) 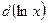 ; д)
; д) 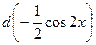 .
.
Задание 2. Найти функцию 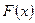 так, что:
так, что:
а) 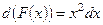 ; б)
; б) 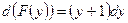 ; в)
; в) 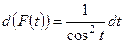 ;
;
г) 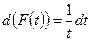 ; д)
; д) 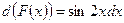 .
.
Задание 3. Найти неопределенные интегралы:
а) 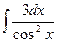 ; б)
; б) 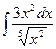 ; в)
; в) 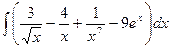 ;
;
г) 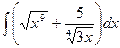 ; д)
; д) 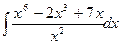 ; е)
; е) 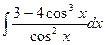 ;
;
ж) 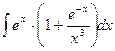 ; з)
; з) 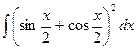 ; и)
; и) 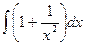 ;
;
к)  ; л)
; л) 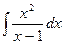 ; м)
; м) 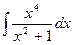 ; н)
; н)  ;
;
о) 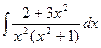 .
.
Раздел 5.2. Основные методы интегрирования.
Заметим, что интегрирование функции - процесс не простой. Или, как говорят, что если дифференцирование – процесс рутинный (т.е. алгоритмизируемый: некоторая дрессировка и нет проблем), то интегрирование – процесс творческий, и некое подобие интуиции появляется после долгой-долгой тренировки: примерно по 100 интегралов на каждый метод, и 101 интеграл берется уже легко.
Имеются лишь отдельные приемы, позволяющие интегрировать отдельные классы функций.
|
|
|
А задача такова: так преобразовать подынтегральное выражение, чтобы интеграл принял вид либо табличного, либо уже известного интеграла.
Непосредственное интегрирование.
Пользуясь таблицей основных элементарных функций, свойствами неопределенных интегралов, выполнив некоторые тождественные преобразования, можно интегрировать некоторые элементарные функции.
 |
Пример:
1. 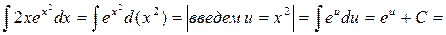
 .
.
2. 
3. 
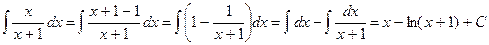 .
.
Замена переменной.
Некоторые интегралы сводятся к табличным удачно придуманной подстановкой. При этом проиcходит замена переменной. Не забудьте в случае достижения результата, вернуться к исходной переменной интегрирования.

Примеры:
1. 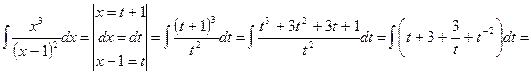
= 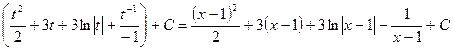 ,
,
2.  ,
,
3. 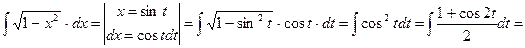
= 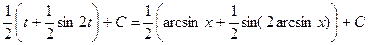 .
.
 |
Интегрирование по частям.
Пусть функции  и
и 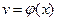 непрерывно дифференцируемы на некотором промежутке.
непрерывно дифференцируемы на некотором промежутке.
Известно,
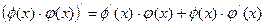 .
.
Проинтегрируем обе части тождества:
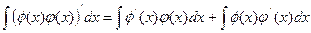 ,
,
получаем:
 ,
,
или, что все равно:
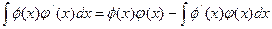 ,
,
или, короче (и чаще используемый вид):
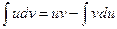 .
.
Последняя формула называется формулой интегрирования по частям. Точнее было бы название – формула частичного интегрирования, но исторически (как часто бывает, и не только в математике) сложилось так.
Суть метода такова: подинтегральное выражение следует представить (по возможности) в виде произведения некоторой функции u на дифференциал dv какой-то другой; получив uv, если повезет, оставшийся в правой части 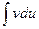 либо уже табличный, либо сводится к табличному другими известными методами. Если с первого раза не повезет (это часто бывает), то пробуйте другие обозначения u и dv.
либо уже табличный, либо сводится к табличному другими известными методами. Если с первого раза не повезет (это часто бывает), то пробуйте другие обозначения u и dv.
При отыскании v по dv достаточно найти одну какую-либо первообразную. Не трудно видеть, что прибавление к ней произвольной постоянной не меняет результата интегрирования, но усложняет промежуточные выкладки.
 |
Пример:
1. 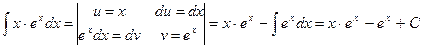 .
.
Попробуйте обозначить: 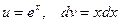 . Разницу увидите сразу.
. Разницу увидите сразу.
2. 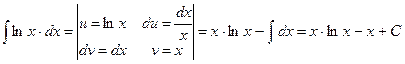 .
.
 А здесь просто нет никакой другой возможности.
А здесь просто нет никакой другой возможности.
Иногда для получения окончательного результата приходится несколько раз последовательно применять формулу интегрирования по частям.
|
|
|
|
|
|


