Сортировка Хоара с выбором медианного элемента

Улучшенные методы сортировки

Сортировка Шелла

Сортировка Шелла — алгоритм сортировки, являющийся усовершенствованным вариантом сортировки вставками. Идея метода Шелла состоит в сравнении элементов, стоящих не только рядом, но и на определённом расстоянии друг от друга. Иными словами — это сортировка вставками с предварительными «грубыми» проходами.

Сортировка Шелла была названа в честь её изобретателя — Да Шелла, который опубликовал этот алгоритм в 1959 году.

Выбор длин промежутков

- Первоначально используемая Шеллом последовательность длин промежутков: в худшем случае, сложность алгоритма составит ;

- предложенная Хиббардом последовательность: .Такая последовательность шагов приводит к алгоритму сложностью ; Массив шагов заполняется перед сортировкой.

- предложенная Седжвиком последовательность: , если i четное и , если i нечетное. При использовании таких приращений средняя сложность алгоритма составляет: 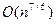, а в худшем случае порядка . Массив приращений заполняется перед сортировкой. Последнее значение массива шаг[s-1], если 3*шаг[s] > N (Если размер массива меньше 3-х шагов).

- Наиболее часто используемая последовательность шагов - изменяется по правилу (для массивов, содержащих более 500 элементов) и (для массивов, содержащих менее 500 элементов). За принимается число элементов массива. Метод заканчивает работу, когда становится меньше 1.

 

Комбинированная сортировка (сортировка «расческой»)

 

Комбинация пузырька и сортировки Шелла. На каждом шаге сравниваются значения отстоящие друг от друга на заданное значение шага , но такое сравнение происходит всего один раз. Как только значение смещения становится равным 1, выполняется сортировка до конца методом пузырька. За принимается число элементов массива.

Пирамидальная сортировка

 

Пирамида – это частично упорядоченное двоичное дерево, элементы которого расположены в узлах дерева по следующему правилу – каждый элемент родительского узла обязательно больше элементов, расположенных в дочерних узлах. Следующий рисунок представляет пирамиду из 15 элементов:

 

Рис. 1

Элементы дерева легко представляются в виде массива – пусть родительский узел имеет индекс , тогда дочерние узлы имеют индексы и . Рассмотренная пирамида может быть представлена массивом:

Индексы

Элементы

 

Т.к. корневой элемент элемент пирамиды всегда является максимальным элементом, то процесс пирамидальной сортировки можно описать следующим образом: поменять верхний элемент пирамиды с нижним элементом и рассматривать в дальнейшем не элементов исходного массива, а элемент. Но при обмене элементов нарушается правило расположения элементов в пирамиде, поэтому после обмена необходимо перестроить пирамиду с элементами и повторять два этих шага, пока пирамида не останется пустой. Таким образом, необходимо написать процедуру, строящую пирамиду для произвольного массива размерности n, далее алгоритм пирамидальной сортировки очень прост. Для формального описания алгоритма назовем процедуру построения пирамиды из массива размерностью N KeyDown(N) – т.к. элемент, находящийся в корне пирамиды может быть и не самым большим, то необходимо опустить этот элемент на нижние уровни пирамиды, чтобы выполнялась частичная упорядоченность. Алгоритм может выглядеть следующим образом:

 

1. KeyDown(N,X); // Построение пирамиды на исходном массиве x.

2. X[1] ßà X[N]; // Обмен первого элемента пирамиды с последним

3. L = N-1; // Изменение размерности пирамиды

4. Пока (L>1) // пока пирамида не пуста

KeyDown(N-1,X);

X[1] ßà X[L];

L = L-1;

5. Конец.

 

Рассмотрим процесс построения пирамиды на произвольном массиве:

Индексы

Элементы

 

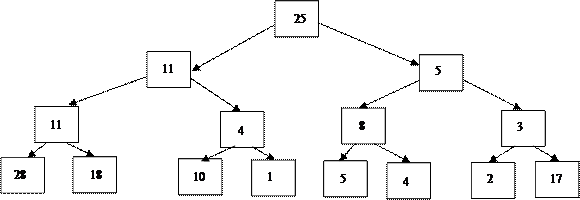
Рис.2

N = 15. Для элементов, находящихся на нижнем уровне не существует дочерних элементов, т.е. эти элементы могут не проверяться на выполнение правила пирамиды, индексы этих элементов от N/2+1 до N. Поэтому построение начинается с элемента с номером N/2, в примере это x[7] = 3, сравним этот элемент с наибольшим из элементов x[14] и x[15], вторая нижняя пирамида остается без изменения, третья и четвертая пирамиды изменяются (см рис. 3).

 

 

 

 

Рис.3

Далее рассматриваем пирамиды с узлами во 2-м и 3-м элементах:

 

 

Рис. 4

 

Рис.5

 

На рис. 4 – 5 изображен процесс построения пирамиды из произвольного массива.

Очевидно, что процедура KeyDown(N,X) должна зависеть еще от одного параметра – номера элемента, для которого строится пирамида.

В общем случае для построения пирамиды с корнем в L-том элементе необходимо выполнять следующие действия: происходит продвижение по дереву вниз, элемент с номером L меняется местами с большим из своих потомков, алгоритм прекращает работу, когда элемент в позиции L больше своих потомков, или когда достигнут нижний уровень.

 

Полный алгоритм пирамидальной сортировки выглядит следующим образом:

 

1. L = (N/2) +1;

2. Пока L>1

L = L-1;

KeyDown(L,N,X); // Построение пирамиды на исходном массиве

3. N1 = N;

4. Пока N1>1

V = x[1]; x[1] = x[N1]; x[N1] = v; // Выталкивание максимального элемента пирамиды в конец массива

N1 = N1 – 1; // Изменение размера пирамиды

KeyDown(L,N1,X);

5. Конец.

 

Сортировка Хоара

Значение какого-нибудь элемента, обычно центрального, принимается за значение опорного элемента. Просматриваются элементы массива. При движении слева-направо ищем элемент больше или равный опорному. А при движении справа-налево ищем элемент меньше или равный опорному. Найденные элементы меняются местами и продолжается встречный поиск.

После этого массив окажется разделенным на две части. В первой находятся элементы меньше либо равные X, а справа - больше либо равные X. Далее алгоритм рекурсивно выполняется для правой и левой частей.

Сортировка Хоара с выбором медианного элемента

Можно улучшить быструю сортировку, выбирая средний элемент таким образом, чтобы его значение было бы действительно близким к серединному значению массива.

Для этого можно пользоваться двумя стратегиями:

1. Выбор среднего значения осуществляется случайным образом (с использованием датчиков случайных чисел и информации о размерности массива). Т.к. разделяющий элемент выбирается при каждом вызове процедуры, случайный выбор может быть наиболее правильным и оградит от появления наихудшего случая – когда медианный элемент оказывается наименьшим или наибольшим.

2. Вторая стратегия состоит в случайном выборе 3-х элементов, по одному из начального, конечного и среднего интервалов сортируемого подмассива. Как разделяющий элемент используется среднее из этих трех чисел.

 

Поделиться:

Воспользуйтесь поиском по сайту: