 |
Случайные величины. 4. Функции распределения вероятностей случайных величин
|
|
|
|
Случайные величины
Случайная величина – это величина, которая в результате испытания может принять одно и только одно возможное значение, причем неизвестно заранее какое именно. Например, количество больных в данном районе, вес и рост человека и т. д.
Случайные величины могут быть дискретными, т. е. принимать отдельные друг от друга возможные значения с определенными вероятностями, которые можно пронумеровать. Например, количество студентов на занятии.
К непрерывным относятся такие случайные величины, которые могут принимать на определенном интервале любые значения. Например, температура тела больного.
Законом распределения случайной величины называется соответствие между возможными значениями случайной величины и соответствующими им вероятностями.
Закон распределения дискретной случайной величины может быть задан таблицей:
| X | x1 | x2 | ¼ | xn |
| p | p1 | p2 | ¼ | pn |
Таблица может быть и бесконечной.
p1 = p(х = x1), p2 = p(х = x2), ¼, pn = p(х = xn).
(х – случайная величина).
События х = x1, х = x2, ¼, х = xn образуют полную группу событий и р1 + р2 + ¼ + рn = 1.
Числовые характеристики случайных величин
Понятия математического ожидания, дисперсии и среднего квадратического отклонения принадлежит к числу наиболее важных, поэтому решению задач на усвоение этих понятий необходимо уделить особое внимание.
Математическое ожидание случайной величины указывает некоторое ориентировочное значение, вокруг которого группируются все значения случайной величины.
Математическим ожиданием дискретной случайной величины называется сумма произведений всех возможных значений величины Х на вероятности этих значений:
|
|
|
M(x) = x1p1 + x2p2 + ¼ + xnpn =  . (1)
. (1)
Для непрерывных случайных величин М(х) = 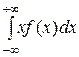 . (3. 13)
. (3. 13)
Дисперсией случайной величины называется математическое ожидание квадрата соответствующего отклонения случайной величины Х от её математического ожидания:
D(x) = M((X – M(x))2) (2)
Для дискретной случайной величины:
D(x) = (x1 – M(x))2× p1 + (x2 – M(x))2× p2 + ¼ + (xn – M(x))2× pn =
= 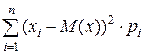 (3)
(3)
Для непрерывной случайной величины
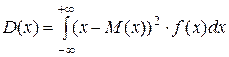 (4)
(4)
При решении задач на отыскание дисперсии непрерывной случайной величины часто вместо этой формулы выгодно использовать равносильную формулу
+¥
D(X) = ò x2f(x)dx – [М(Х)]2. (5)
-¥
Аналогичное замечание относится и к случаю, когда пределы интегрирования a и b. Рекомендуем вывести эту формулу самостоятельно (в порядке упражнения). Для того чтобы из первой формулы получить вторую, надо возвести в квадрат разность, стоящую под знаком интеграла, и разбить полученный интеграл на три интеграла; затем следует вынести за знак интеграла постоянные величины (математическое ожидание есть постоянная величина) и принять во внимание, что 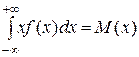 по определению математического ожидания непрерывной случайной величины;
по определению математического ожидания непрерывной случайной величины; 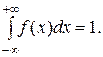
Дисперсия характеризует меру разброса случайной величины около её среднего значения.
Средним квадратическим отклонением случайной величины называют квадратный корень из дисперсии:
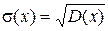 (6)
(6)
4. Функции распределения вероятностей случайных величин
|
|
|
Для количественной характеристики распределения случайных величин вводится понятие функции распределения F(x).
Определение. Функцией распределения случайной величины Х называется функция F(x), равная вероятности того, что случайная величина Х приняла значение меньшее наперёд заданного х:
F(x) = p(X < x).
При любом значении х функция распределения равна сумме вероятностей всех значений Х, меньших х.
Свойства функции распределения.
1) 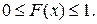
2) F(x) – неубывающая функция.
Следствие 1. Вероятность попадания случайной величины в полуинтервал [a, b) равна приращению функции распределения на этом отрезке:
Р(а £ х < b) = F(b) – F(a). (7)
Следствие 2. Вероятность того, что непрерывная случайная величина X примет какое-либо заранее заданное значение, равна нулю:
Р(Х = а) = 0.
Определение. Плотность вероятности случайной величины X равна производной её функции распределения:
f(x) = F'(x) (8)
Это положительная функция f(x) ³ 0, обладающая свойством (условие нормировки плотности вероятностей):
 (9)
(9)
Вероятность того, что непрерывная случайная величина примет значение, заключённое между а и b равна интегралу от её плотности вероятности, взятому от а до b:
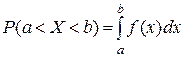 (10)
(10)
Нормальное распределение (закон Гаусса)
Нормальный закон распределения играет огромную роль в медико- биологических наблюдениях и экспериментах. При действии большого числа случайных факторов, каждый из которых сам по себе оказывает независимо от других незначительное действие на случайную величину, последняя подчиняется нормальному закону.
Для нормального распределения, имеющего математическое ожидание m и среднее квадратическое отклонение s, плотность распределения имеет вид:
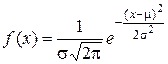 . (11)
. (11)
1. Тема 4: Механика жидкостей и газов. Биомеханика. Акустика.
|
|
|
2. Курс: первый семестр: первый
3. Продолжительность лекции: 2 часа
4. Контингент слушателей: студенты
5. Учебная цель: изучение законов механики жидкостей и газов
6. Иллюстративный материал и оснащение: интерактивная доска
7. Подробный план:
1) Физические методы, как объективный метод исследования закономерностей в живой природе.
2) Механические волны. Уравнение плоской волны.
3) Звук. Объективные (физические) характеристики звука. Субъективные характеристики, их связь с объективными. Закон Вебера-Фехнера.
4) Ультразвук, физические основы применения в медицине.
5) Физические основы гемодинамики. Вязкость. Методы определения вязкости жидкостей. Стационарный поток, ламинарное и турбулентное течения. Формула Ньютона, ньютоновские и неньютоновские жидкости. Формула Пуазейля. Число Рейнольдса. Гидравлическое сопротивление в последовательных, параллельных и комбинированных системах трубок. Разветвляющиеся сосуды.
6). Закон Гука. Модуль упругости. Упругие и прочностные свойства костной ткани. Механические свойства тканей кровеносных сосудов.
8. Методы контроля знаний и навыков: традиционные методы контроля.
9. Литература: см. в приложении.
|
|
|


