 |
Единичные показатели надежности
|
|
|
|
Единичные показатели надежности
Показатели безотказности: вероятность безотказной работы, средняя наработка до отказа, средняя наработка на отказ, гамма-процентная наработка до отказа, интенсивность отказов, параметр потока отказов, средняя доля безотказной наработки, плотность распределения времени безотказной работы.
Показатели долговечности: средний ресурс, гамма-процентный ресурс, назначенный ресурс, средний срок службы, гамма-процентный срок службы, назначенный срок службы.
Показатели ремонтопригодности: вероятность восстановления работоспособного состояния, среднее время восстановления работоспособного состояния, интенсивность восстановления.
Показатели сохраняемости: средний срок сохраняемости, гамма-процентный срок сохраняемости.
Комплексные показатели надежности
коэффициент готовности (вероятность того, что объект окажется в работоспособном состоянии в произвольный момент времени, кроме планируемых периодов, в течение которых применение объекта по назначению не предусматривается), коэффициент оперативной готовности, коэффициент технического использования (отношение математического ожидания интервалов времени пребывания объекта в работоспособном состоянии за некоторый период эксплуатации к сумме математических ожиданий интервалов времени пребывания объекта в работоспособном состоянии, простоев, обусловленных техническим обслуживанием и ремонтов за тот же период эксплуатации), коэффициент планируемого применения (доля периода эксплуатации, в течение которой объект не должен находиться в плановом ТО или ремонте), коэффициент сохранения эффективности.
|
|
|
Академический подход претендует на формализацию любого показателя надежности.
Модельные функции распределения и функции внешних условий
В разделе приведён экскурс в разделы математики, использующиеся в теории надёжности.
Теория вероятностей – это раздел математики, изучающий закономерности в случайных явлениях. Ее возникновение датируется серединой XVII века и в первую очередь связано с именами таких ученых, как Х. Гюйгенс (1629-1695), Б. Паскаль (1623-1662), П. Ферма (1601-1665), Я. Бернулли (1654-1705).
Комбинаторика – раздел теории вероятностей, в котором изучаются вопросы, связанные с составлением комбинаций из конечного множества элементов, подчиненным тем или иным условиям. Впервые она была серьезно рассмотрена немецким философом и математиком Г. Лейбницем (1646-1716), опубликовавшим в 1666г. работу «Об искусстве комбинаторики». Как и всякий раздел математики, комбинаторика стремится разложить некую сложную ситуацию-суперпозицию на элементарные составляющие. Базовыми понятиями комбинаторики являются: элементарное случайное событие и сложное случайное событие (или короче: случайное событие). Элементарное случайное событие – это элементарный единичный исход случайного эксперимента. Множество всех элементарных событий обычно обозначается Ω. Всякое подмножество множества Ω элементарных событий называется случайным событием.
Примером случайного события в электроэнергетике может быть повреждение отдельных элементов энергосистемы в результате износа оборудования, короткое замыкание, изменение нагрузки подстанций, грозовые перенапряжения и т. д. Случайное событие – это явление, с одной стороны не являющееся достоверным, с другой стороны – не являющееся в принципе невозможным.
Формула Бернулли, формула Пуассона, распределение Гаусса
Формула Бернулли (используется при относительно небольшом количестве опытов)
|
|
|
Если вероятность p {\displaystyle p} p наступления события A {\displaystyle A} в каждом испытании постоянна, то вероятность Pnk P k, n {\displaystyle P_{k, n}} PPтого, что событие A {\displaystyle A} наступит ровно k k {\displaystyle k} kраз в n n {\displaystyle n} независимых испытаниях, равна:
P k, n = C n k ⋅ p k ⋅ q n − k {\displaystyle P_{k, n}=C_{n}^{k}\cdot p^{k}\cdot q^{n-k}}
q = 1 − p {\displaystyle q=1-p}
Распределение Пуассона (используется для анализа распределений исходов сотен и тысяч опытов)
Распределение получается при достаточно большом количестве (N больше 100) одинаковых опытов, и определяет вероятность наступления некоторого бинарного события k раз в этой серии опытов, причем вероятность p1 наступления события в элементарном опыте – одинакова и мала.
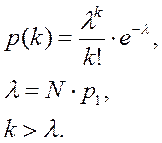
Простейший поток событий – последовательность событий, которые наступают в случайные моменты времени на определенном временном интервале, обладающая следующими свойствами: стационарность (вероятность появления некоторого числа событий на некотором интервале времени зависит только от длины этого интервала и не зависит от начала интервала), отсутствие последействия (вероятность появления некоторого числа событий на последующем отрезке времени не зависит от появления \ не появления событий на предыдущем отрезке для двух любых неперекрывающихся временных отрезков), ординарность (в один мгновенный момент времени не может появиться более одного события).
Вероятность появления m событий простейшего потока событий на отрезке времени Т вычисляется по формуле:
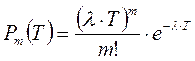
Где λ – интенсивность событий, т. е. среднее число событий потока в единицу времени.
Распределение Гаусса
Согласно центральной предельной теореме (из теории вероятностей) сумма достаточно большого количества слабо зависимых случайных величин, имеющих примерно одинаковые масштабы (ни одно из слагаемых не доминирует, не вносит в сумму определяющего вклада), имеет распределение, близкое к нормальному.
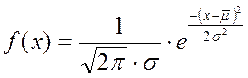
Экспоненциальное распределение
Часто используется как составное для формирования моделей отказов стареющих объектов (случайные процессы с накоплением, которые представляются как многостадийные, причем каждая стадия описывается экспоненциальным распределением). В качестве примера можно привести длительность безотказной работы одного высоковольтного выключателя с ограниченным числом отключений КЗ. При этом длительность периода между смежными КЗ подчинена экспоненциальному распределению. Если же рассматривается серия выключателей, то график распределения отказов будет U-образный (на первом этапе будет выявлен брак, затем будет установившаяся динамика отказов, а затем – отказы на больших временах).
|
|
|
Распределение Вейбулла
Пусть распределение случайной величины X {\displaystyle X} задаётся плотностьюf X ( x ) {\displaystyle f_{X}(x)}, имеющей вид:
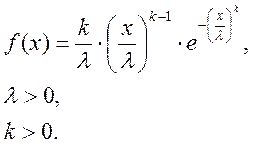
Если величину X принять за наработку до отказа, тогда получается распределение, в котором интенсивность отказов пропорциональна времени. Тогда:
- k < 1 показывает, что интенсивность отказов уменьшается со временем
- k = 1 показывает, что интенсивность отказов не меняется со временем
- k > 1 показывает, что интенсивность отказов увеличивается со временем
В материаловедении коэффициент k известен как модуль Вейбулла.
Распределение Вейбулла очень широко используется: в анализе надёжности и отказов, в электротехнике для представления перенапряжения, возникающего в электрических цепях, в промышленной инженерии, в прогнозировании погоды и гидрологии (например, для описания распределения скорости ветра как распределения, обычно совпадающего с распределением Вейбулла в ветроэнергетике), в прогнозировании технологических изменений и пр.
Гамма-распределение. Распределение Эрланга
,
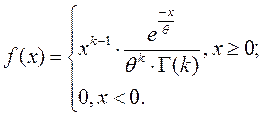Где Г(к) – гамма-функция Эйлера: 
, которую в контексте стохастического подхода к проблеме надежности сложных систем следует рассматривать в качестве обобщения понятия «факториал».
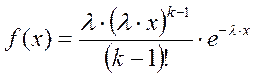
Коэффициент интенсивности отказов определяется следующим образом:
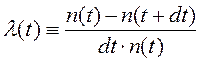
Фактически он представляет собой скорость относительного выхода из строя рассматриваемой выборки образцов. Ниже представлена классическая экспериментальная зависимость интенсивности отказов от времени:
|
|
|
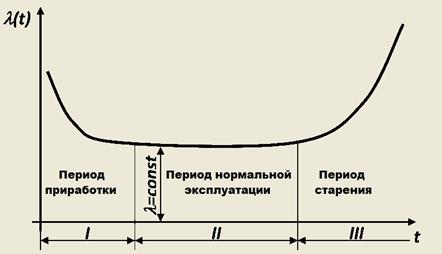
Рисунок 3 Экспериментальная кривая интенсивности отказов
Время можно условно разделить на три характерных участка: период приработки, период нормальной эксплуатации и период старения изделия. Период приработки имеет повышенную интенсивность отказов, вызванную приработочными отказами, обусловленными дефектами производства, монтажа и наладки. Иногда с окончанием этого периода связывают гарантийное обслуживание объекта, когда устранение отказов производится изготовителем. В период нормальной эксплуатации интенсивность отказов практически остаётся постоянной, при этом отказы носят случайный характер и появляются внезапно, прежде всего, из-за случайных изменений нагрузки, несоблюдения условий эксплуатации, неблагоприятных внешних факторов и т. п. Именно этот период соответствует основному времени эксплуатации изделия. Возрастание интенсивности отказов относится к периоду старения и вызвано увеличением числа отказов из-за износа, деградации и других причин, связанных с длительной эксплуатацией.
Функция распределения по интенсивности отказов рассчитывается следующим образом:
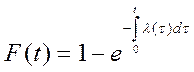, причем 
.
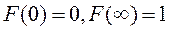Функция надежности определяется следующим образом:
.
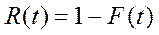Структурная надежность
Изучение структурной надежности сложных систем связано с процессом составления структурных схем этих систем, с последующим их анализом. Под термином «структурная схема» понимается условное графическое изображение элементов схемы или системы и связей между ними. Понятие структурной схемы широко используется в ряде отраслей знаний: в теории связи, в теории автоматического регулирования, в экономике, при социологических исследованиях и др. Например, в теории автоматического регулирования структурные исследования были проведены академиком Б. Н. Петровым и И. И. Гальпериным. В теории связи выросло целое научное направление – структурная теория сетей связи, наиболее полно представленная работой Г. Н. Поварова. Теория графов, как и теория надежности в целом, не обладает устоявшейся терминологией. В различных публикациях под одними и теми же терминами понимаются разные сущности.
Основным и общим во всех работах, связанных со структурными исследованиями, является стремление очистить объект исследования от всего вторичного, рассмотреть лишь его наиболее характерные признаки. Например, при структурном исследовании систем автоматического регулирования в них не остается иного содержания, кроме связей, их числа, дифференциального порядка, знака и конфигурации. Структурная схема позволяет изучать объект в наиболее общем и чистом виде. Это обстоятельство и побуждает перенести методы структурного анализа в теорию надежности. Кроме того, усложнение систем требует рассмотрения таких структурных вопросов, как число возможных транзитных путей между двумя заданными элементами системы, о минимальном и максимальном числе звеньев в этих путях, о связности сети и пр. Уделяя основное внимание выявлению взаимных связей между элементами системы, тем самым выдвигая на первое место структуру системы, а не состав ее отдельных компонент, мы получим возможность единообразно исследовать различные по своей природе системы. Попытки получения обобщений такого рода позволяют использовать в теории надежности основные достижения различных отраслей науки.
|
|
|
Основным объектом структурного анализа является т. н. граф, а также ребра графа и вершины графа. Существует строгое математическое определение графа, но данный материал не ставит задачей углубленное внимание этим вопросам, поэтому ограничимся качественным определением: граф – это абстрактный плоский математический объект, представляющий собой множество вершин и набор рёбер, т. е. соединений между парами вершин. Вершины графа, точки физического сочленения его ребер, могут, напр., представлять собой источники сигналов, приемники сигналов и пр.
Графы по видам ребер бывают неориентированными, частично ориентированными, ориентированными. Здесь подразумевается эквивалентность или неэквивалентность направлений от одной вершины ребра к другой.
Два графа называются изоморфными, если существует перестановка вершин, при которой они совпадают. Иначе говоря, два графа называются изоморфными, если существует взаимно-однозначное соответствие между их вершинами и рёбрами, которое сохраняет смежность и инцидентность (принадлежность вершин своим ребрам). Иногда в структурном анализе приходится отображать множество вершин во множество граней, и наоборот.
Изучение структуры той или иной схемы равносильно изучению структуры графов. Граф называется планарным, если он может быть изображен на плоскости бузе пересечений ребер в точках, не являющихся вершинами графа, в противном случае граф является не планарным.
Путь в графе – множество проходимых последовательных ребер, в котором ни одна вершина графа не проходится двукратно. Пути бывают непосредственными (одно ребро) и транзитными (несколько ребер). Матрица непосредственных путей составляется следующим образом: элемент, принадлежащий i-той строке и j-тому столбцу, будет равен единице (или в более общем случае некоторому натуральному числу, отличному от нуля), если из вершины i к вершине j имеется непосредственный путь, и равен нулю в противном случае. Соответственно, порядок такой матрицы равен числу вершин графа, в общем случае она несимметричная, т. к. граф может быть ориентированным.
Основной вопрос, который приходится решать в структурном анализе – подсчет числа путей между двумя вершинами графа, анализ их состава, определение максимальных и минимальных путей. Все остальные задачи являются производными от этой основной.
Наиболее часто в инженерной практике рассматривают последовательное, параллельное, смешанное (последовательно-параллельное и параллельно-последовательное) соединение элементов, а также схемы типа «K из N», мостиковые соединения.
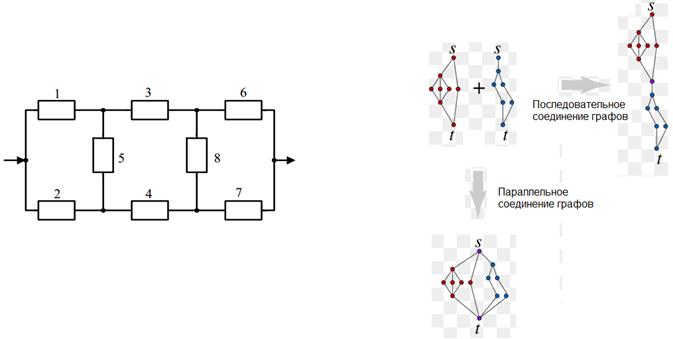
Рисунок 4 Примеры графов: мостиковое соединение (слева), варианты смешанного соединения (справа)
Следует упомянуть формулу полной вероятности и основанную на ней т. н. теорему разложения на множители. Они играют большую роль при анализе надежности сложных схем, поскольку позволяют свести любую сложную схему к совокупности элементарных. Метод оценки надежности, основанный на формуле полной вероятности, весьма прост и нагляден в расчетах, не требует значительных ресурсов ЭВМ для простых схем. Для схем сложной конфигурации реализация этого метода осложняется неоднозначностью выбора элементов, относительно которых производится разложение.
Формула полной вероятности для определения надежной работы схемы интерпретируется следующим образом: вероятность любого события (например, вероятность работы некоторой системы относительно узла) вычисляется как сумма произведений вероятностей несовместимых (взаимоисключающих) гипотез и вероятности события (работы оставшейся части цепи) при этой гипотезе. Причем в качестве гипотезы рассматривается либо работа, либо отказ любого элемента цепи. Применяя формулу полной вероятности к расчету вероятности безотказной работы любой схемы, можно сформулировать теорему разложения на множители: надежность цепи с избыточностью равна произведению вероятности безотказной работы i-го элемента цепи на вероятность безотказной работы оставшейся цепи (в этом случае точки подключения i-го элемента замкнуты накоротко), плюс произведение вероятности отказа того же элемента на вероятность безотказной работы оставшейся цепи (точки подключения i–го элемента разомкнуты). Т. е. для выделенного в схеме элемента рассматриваются две независимые гипотезы.
Пример реального графа:
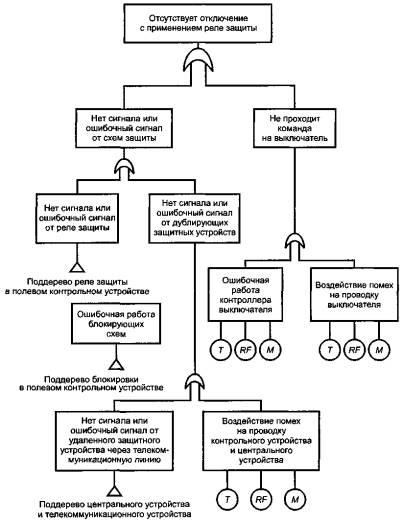
Рисунок 5 Пример дерева неисправностей
|
|
|
