Теорема Лиувилля. Всякий объем фазового пространства при своем движении соответствующего изменению состояния системы остается по величине неизменным.

Теорема Лиувилля. Всякий объем фазового пространства при своем движении соответствующего изменению состояния системы остается по величине неизменным.

Другими словами, если в начальный момент времени фазовые точки q_i, p_i непрерывно заполняли некоторую область G в фазовом пространстве, а с течением времени перешли в другую область G_t этого пространства, то, согласно теореме Лиувилля, соответствующие фазовые объемы равны между собой.

Таким образом, движение точек, изображающих состояния системы в фазовом пространстве, подобно движению несжимаемой жидкости. Это означает, что плотности точек в этих объемах одинаковы и пропорциональны 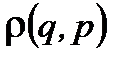. Отсюда следует, что функция распределения  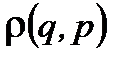постоянна вдоль фазовых линий, соответствующих движению (изменению состояния) рассматриваемой системы:

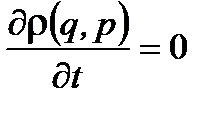                                                              (1. 39)

Для того, чтобы функция распределения 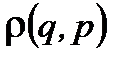 была постоянной во времени в разрешенной области фазового пространства, она должна зависеть от такой комбинации переменных p_x, p_y, p_z, которая не зависит от t, т. е. от интегралов движения (инвариантов). Такие инварианты (интегралы движения) хорошо известны. Это энерги я, импульс (3 компоненты) и момент импульса (3 компоненты). Импульс и момент импульса связаны с движением тела или газа как целого, поэтому в системе отсчета, где сосуд с газом покоится, импульс и момент импульса можно исключить из рассмотрения.

Таким образом, для идеального газа и вообще для любой квазизамкнутой системы функция распределения 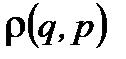, описывающая статистическое состояние системы, зависит только от энергии. Вывод -   энергия в статистике приобретает исключительную роль.

§1. 7. Функция распределения по энергиям.

Учитывая определяющую роль энергии, естественно перейти от вероятности попадания молекулы в объем 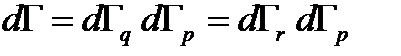 к вероятности для молекулы иметь энергию E. Для идеального газа нет необходимости рассматривать пространственную часть объема фазового пространства , т. к. энергия не зависит от координат для невзаимодействующих молекул. Ищем вероятность состояния молекулы с энергией в интервале от E до (E+dE), . Для определенной скорости v, или импульса p, область, соответствующая диапазону (E ¸ E + dE), имеет вид тонкого шарового слоя, радиусом  

Вероятность того, что энергия молекулы находится в диапазоне (E ¸ E + dE), равна по теореме о сложении вероятностей

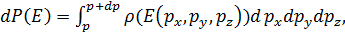                   (1. 40)

где интегрирование ведется по шаровому слою от p до p + dp. Так как шаровой слой очень тонкий, то 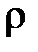 внутри можно считать постоянной. Тогда

.                                        (1. 41)

Здесь введено обозначение 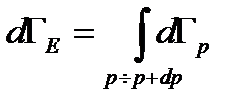   - объем шарового слоя с радиусом p. Объем шара в импульсном пространстве равен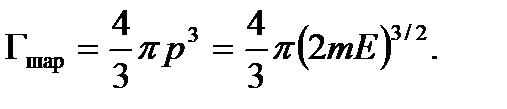                                                    

Объем шарового слоя равен 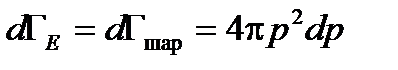. Учитывая, что , запишем 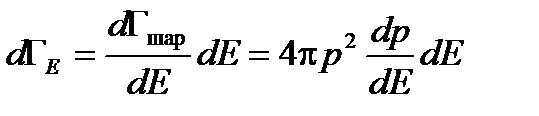. Итак, вероятность для молекулы идеального газа иметь энергию в интервале от E до E + dE равна

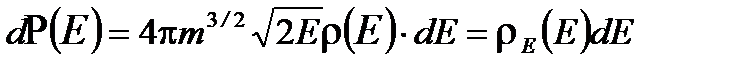                              (1. 42)

Функция распределения молекул по их энергиям, следовательно, определяется соотношением  .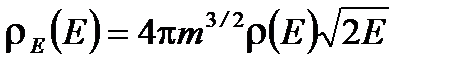                                    

Важно отличать друг от друга две функции распределения. Функция микрораспределения  представляет собой плотность вероятности обнаружить систему в единице фазового объема с координатами q и p.

Функция макрораспределения представляет собой плотность вероятности обнаружить систему в состоянии с определенной энергией при всех координатах и импульсах, соответствующих этой энергии (шаровой слой в фазовом пространстве).

Зависимость 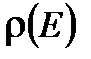 от энергии.   Используя вероятностные соображения, можно найти зависимость функции  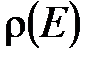от энергии. Выделим в газе квазизамкнутую подсистему из двух невзаимодействующих молекул. Энергия подсистемы- аддитивная величина - 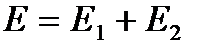. Функция распределения подсистемы по теореме умножения вероятностей равна 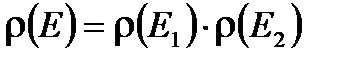.                                                    Таким образом, функция распределения не аддитивная величина. Так как всегда удобнее работать с аддитивными величинами, то будем в квазизамкнутой системе рассматривать логарифм распределения, который есть аддитивная величина от энергии:

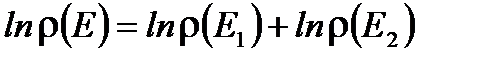.                                              (1. 43)

Выражение (1. 43) выполняется только тогда, когда 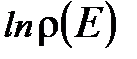 является линейной функцией энергии E

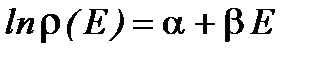 ,                                                      (1. 44)

где a и b неизвестные пока постоянные. Итак, в общем случае

.                                                      (1. 45)

До сих пор рассматривали идеальный газ. Однако все эти рассуждения могут быть применены к произвольному макроскопическому телу (неидеальные газы, жидкость, твердое тело).  Для этого надо выразить  дифференциал dG_E через дифференциал dE и ввести функцию макрораспределения подсистемы по энергиям:

, , .

 

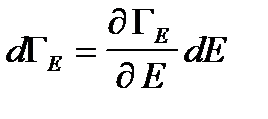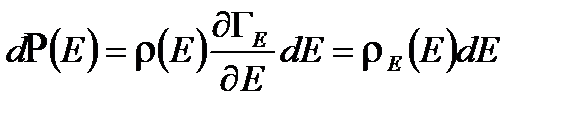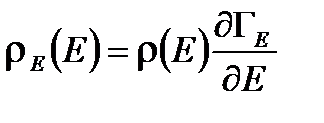⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: