 |
Основные положения, выносимые на защиту 7 глава
|
|
|
|
В то время, как на выходе одиночного усилительного каскада уровни интермодуляционных колебаний в десятки раз меньше уровней основных колебаний, на выходе N каскадного тракта амплитуды интермодуляционных колебаний могут достигать уровней, не намного меньших уровней основных колебаний.
На следующем рисунке 2.5.5 приведены графики, с помощью которых определена зависимость динамического диапазона N каскадного усилительного тракта от числа содержащихся в нем усилительных каскадов. Графики построены для частного случая К = 2 и D u = 1. Из приведенного рисунка видно, что каждый дополнительный каскад приводит к уменьшению динамического диапазона на величину порядка 4 дБ. Аналогичным образом было определено уменьшение динамического диапазона для значений К = 5 и К = 10, которые оказались равными
соответственно 9 дБ и 13 дБ. Для К ³ 2 эмпирическим путем было найдено нижеприведенное простое выражение, позволяющее производить оценку снижения динамического диапазона в зависимости от числа каскадов в тракте N и их коэффициента усиления К.
| * |
| * |
| * |
| * |
| * |
| * |
| * |
| * |
| * |
| * |
| * |
| * |
| * |
| * |
| * |
| * |
| * |
| * |
| * |
| * |
| * |
| * |
| * |
| * |
| * |
| * |
| * |
| * |
| * |
| * |
| U 2,i U 2f2-f1 |
| 1,0 |
| 0,5 |
| 0,2 |
| 0,1 |
| 0,05 |
| 0,02 |
| 0,01 |
| 0 1 2 3 4 5 6 7 8 9 10 N |
| U 1,i =0,5 |
| U 1,i =0,2 |
| U 1,i=0,02 |
| U 1,i=0,005 |
| U 1,i =0,5 |
| U 1,i =0,2 |
| U 1,i=0,02 |
| U 1,i=0,005 |
Рис. 2.5.4. Зависимость амплитуд основных (°) и интермодуляционных (*) колебаний вида (2f2-f1) при бигармоническом равноуровневом входном воздействии от числа усилительных каскадов в тракте (К = 2)
[дБ]. (2.5.10)
| U 2f2-f1 |
| 4∙10-5 |
| 2∙10-5 |
| 10-5 |
| 5∙10-6 |
| 2∙10-6 |
| 10-6 |
| 10-3 |
| 2∙10-3 |
| 5∙10-3 |
| 10-2 |
| 2∙10-2 |
| U l,i |
| N=5 |
| N=4 |
| N=3 |
| N=2 |
| N=1 |
| N=64дБ |
| N=69дБ |
| N=73дБ |
| N=77дБ |
| N=81дБ |
|
|
|
Рис. 2.5.5. Зависимость динамического диапазона тракта от числа усилительных каскадов (К = 2)
Выражение (2.5.10) дает следующие значения уменьшения динамического диапазона на один усилительный каскад для значений
К = 2, К = 5 и К = 10:
DD2 = -3,91 дБ; DD5 = -9,08 дБ и DD10 = -12,99 дБ, что хорошо согласуется со значениями потерь динамического диапазона, полученными в вычислительных экспериментах.
При полигармоническом воздействии колебаний большого уровня моделирование многокаскадного усилительного тракта КВ РПУ целесообразно
производить в целом как безынерционного усилителя-ограничителя, ПХ которого соответствует результирующей ПХ ГТ РПУ.
2.6. Аналитическая модель усилителя-ограничителя
Усилитель-ограничитель (УО) [83] является одним из основных элементов, входящих в состав различного рода радиоаппаратуры. Например, в режиме достаточно глубокого ограничения обычно работают усилители мощности на выходе передатчиков сигналов с частотной и фазовой модуляцией. УО используются в демодуляторах частотно-модулированных и фазомодулированных сигналов для нормирования уровня колебаний, подаваемых на вход детектора. Мало чем отличается ПХ УО от ПХ АЦП сигналов с ограниченным динамическим диапазоном, который при воздействии на его вход напряжения, превышающего допустимый уровень, начинает работать в режиме насыщения.
Очень часто встречается проблема определения спектрального состава колебания на выходе УО, когда на его вход поступает большое число гармонических сигналов разной частоты. Для случая одиночного гармонического входного воздействия на УО задача определения спектра выходного колебания была полностью решена академиком А. И. Бергом в ходе разработки им теории ламповых генераторов. Для аппроксимации ПХ УО Берг использовал кусочно-линейную функцию. Метод Берга является классическим и описан во всех учебниках по радиотехническим цепям и сигналам (см., например, [55]). К сожалению, этот метод не дает возможности анализировать работу УО, когда на его вход одновременно воздействуют два или большее число сигналов. Для решения этой задачи представим кусочно-линейную ПХ УО комбинированной функцией в виде суммы линейной функции и ряда Фурье.
|
|
|
ПХ УО в случае кусочно-линейной аппроксимации описывается следующим образом:
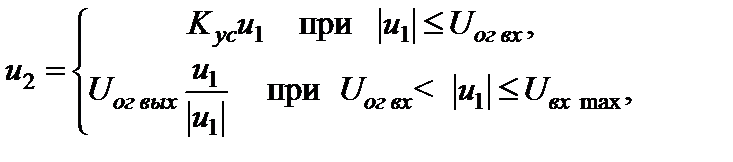(2.6.1)
где Kус – коэффициент усиления УО при работе в пределах линейного участка ПХ,
U ог вх – порог ограничения сигнала по входу, U ог вых – порог ограничения сигнала по выходу, U вх max – максимально допустимое напряжение на входе УО.
Очевидно, что U ог вых = Kус U ог вх.
Произведем нормирование осей координат, соответствующих входному и выходному колебаниям, следующим образом:
. (2.6.2)
В этом случае (2.6.1) принимает вид:
(2.6.3)
где 
.
ПХ УО при такого рода кусочно-линейной аппроксимации изображена функцией y 1(x) на рисунке 2.6.1.
Проведем прямую y 2(x) = x, и разность функций y 1(x) – y 2(x) = D y (x) представим рядом Фурье на интервале – 1 < x < 1:
|
В этом случае аналитическая модель УО описывается выражением:
. (2.6.4)
Аналитическая модель (2.6.4) лишена недостатков, присущих кусочно-линейной модели (2.6.3), хотя полностью ей соответствует на интервале
– 2 + α < x < 2 – α.
| D y = y 1– y 2 |
| y 1 (x) |
| (– 2+ α) |
| – 1 |
| – α |
| α |
| (2 – α) |
| – 1 |
| y |
| x |
| – 2 |
| y 2= x |
Рис. 2.6.1. Представление проходной характеристики усилителя-ограничителя при кусочно-линейной аппроксимации (y 1) в виде суммы линейной (у 2) и разностной (D y) функций
Пусть на вход УО одновременно поступает I гармонических колебаний. Тогда напряжение на входе УО u 1(t) с учетом возможного постоянного смещения U 1,0 рабочей точки на ПХ можно записать в следующем виде:
, (2.6.5)
где Θ 1,i = 2π f 1,i t + φ 1,i, f 1,i – частота i – го колебания, φ 1,i – его начальная фаза.
Произведем нормирование оси абсцисс и оси ординат согласно отношениям (2.6.2).
Тогда входное воздействие на УО описывается выражением:
,
где 
и 
Известное равенство [134]
,
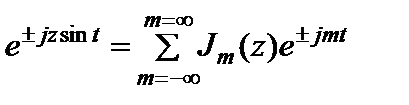где J m(z) – функция Бесселя первого рода m – го порядка, позволяет в этом случае нормированное колебание y (t) на выходе УО представить на интервале
|
|
|
– 2 + α < x < 2 – α в следующем виде:
(2.6.6)
Это выражение свидетельствует о том, что в результате взаимодействия отдельных гармонических составляющих спектра входного колебания УО на его выходе образуются гармоники и интермодуляционные составляющие сколь угодно высоких порядков. Первый член суммы (2.6.6) содержит транслируемый через УО на его выход спектр входного колебания за счет линейной составляющей ПХ с коэффициентом передачи равным единице и без каких-либо искажений. Второй член этой суммы содержит гармоники и интермодуляционные составляющие нечетных порядков (включая первый), а третий член – четных порядков.
С помощью выражения (2.6.6) можно получить любые характеристики УО.
Например, амплитудная характеристика УО в случае гармонического входного воздействия x (t) = X 0 + X sin(2π f t + φ) для | X 0 ± X | < 2 – α может быть получена из (2.6.6) при I = 1 и n1 = ± 1:
. (2.6.7)
С учетом того, что для линейного участка ПХ выполняется неравенство
| X 0 ± X | ≤ α и Y = X /α, из выражения (2.6.7) следует равенство:
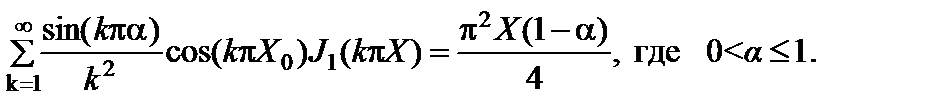(2.6.8)
Если начальное смещение рабочей точки ПХ УО отсутствует, то X0 = 0 и (2.6.8) можно переписать в более простом виде:
(2.6.9)
В свою очередь, при X стремящемся к нулю функция Бесселя первого рода первого порядка J 1(kπ X) стремится к значению половины своего аргумента kπ X /2, и из (2.6.9) можно получить равенство
(2.6.10)
которое совпадает с (1.441) в [139].
Для случая гармонического входного воздействия при кусочно-линейной ПХ УО амплитудная характеристика УО может быть получена также и обычным путем с помощью модели Берга [127]:
(2.6.11)
Q 1 - угол отсечки положительного полупериода колебаний,
Q 2 - угол отсечки отрицательного полупериода колебаний.
Результаты, полученные с помощью выражения (2.6.11), как и следовало ожидать, совпадают с результатами, рассчитанными по формуле (2.6.7).
В случае гармонического воздействия на вход УО из (2.6.6) можно получить следующие выражения для расчета четных и нечетных гармоник колебания на его выходе:
|
|
|
(2.6.12)
Из (2.6.12) следует, что при X 0 = 0 четные гармоники на выходе УО отсутствуют.
Из физических соображений следует, что при X 0 = 0 и X < a (линейный режим работы) на выходе УО отсутствуют и все нечетные гармоники за исключением первой, т. е. справедливо равенство:
(2.6.13)
При α ≠ 0 и X 0 = a из (2.6.12) можно получить выражение:
(2.6.14)
откуда с учетом (2.6.13) следует, что при X £ 2a выполняется равенство Y 2n+1 = 0. Иначе говоря, если смещение рабочей точки равно порогу ограничения по входу, то, пока уровень сигнала не достигнет второго порога ограничения, т. е. пока X ≤ 2α, нечетные гармоники выше первого порядка на выходе УО будут отсутствовать.
Аналогичный вывод следует и из модели Берга, описывающей гармоники усилителя-ограничителя выражением
Действительно, при заданных выше условиях угол отсечки Q = p / 2 и все нечетные гармоники, за исключением первой, равны нулю.
Если X 0 = 0 и a → 0, то УО превращается в идеальный ограничитель (ИО). Следует заметить, что модель Берга не может быть использована для расчета гармоник колебания на выходе ИО. Модель (2.6.4) способна решить эту задачу. Для ИО из (2.6.7) следует равенство:
В этом случае при гармоническом входном воздействии колебание на выходе ИО имеет вид меандра. Для меандра можно определить значения амплитуд нечетных гармоник выходного колебания [55]:
. 
(2.6.15)
С учетом этого, для основной гармоники при n = 1 справедливо равенство:
(2.6.16)
которое является частным случаем выражения (6.4.3) в [139].
Если имеет место ИО, то с учетом (2.6.15) можно записать равенство
которое также является частным случаем (6.4.3) в [139].
Таким образом, математическая модель УО (2.6.4) при гармоническом воздействии дает те же результаты, что и кусочно-линейная модель (2.6.3). Модель (2.6.4) правомочна и в случае ИО. Кроме того, модель УО, описываемая выражением (2.6.4), в отличие от кусочно-линейной модели (2.6.3), позволяет исследовать нелинейные явления не только при одиночном гармоническом, но и при полигармонических входных воздействиях.
Рассмотрим непосильный для кусочно-линейной модели, но практически важный случай разноуровневого бигармонического входного воздействия на УО, когда выполняется условие X1 << X2. Согласно (2.6.6), при малых значениях X1 амплитуда сигнала Y1 описывается выражением:
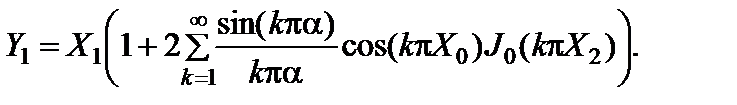(2.6.17)
Из уравнения (2.6.17) следует, что характеристика блокирования УО при кусочно-линейной ПХ имеет следующее выражение:
Так как при X 0 = 0 и при работе в пределах линейного участка ПХ блокирование отсутствует, то можно записать равенство
из которого с учетом (2.6.10) следует правомочность выражения
для α ≤ 1 и X < α. (2.6.18)
|
|
|
Пусть частота f 2 большего по уровню колебания превышает частоту f 1 колебания с меньшим уровнем. В этом случае практический интерес представляет
собой интермодуляция третьего порядка вида 2 f 2 – f 1, уровень которой является наибольшим среди других интермодуляционных компонентов. Если X 1 << α, то амплитуда интермодуляционного колебания вида 2 f 2 – f 1, согласно выражению (2.6.6), определяется с помощью уравнения
(2.6.19)
В этом случае отношение амплитуды интермодуляции 
к амплитуде меньшего колебания Y 1 на выходе УО равно
.
Принимая во внимание известное [134] равенство
,
можно выражение (2.6.19) для ИО, когда α = 0 и X0 = 0, переписать в виде
(2.6.20)
С учетом ранее полученного уравнения (2.6.16), равенство (2.6.20) может быть преобразовано следующим образом:
Это выражение, согласно (2.6.17), можно записать в виде:
Последнее уравнение говорит о том, что, если на входе ИО отношение амплитуд сигналов X 1 / X 2 стремится к нулю, то амплитуда интермодуляционной составляющей на выходе ИО с частотой (2 f 2 – f 1) стремится к значению амплитуды меньшего колебания Y 1, что и наблюдается на практике.
Рассмотрим случай равноуровневого бигармонического воздействия на вход
УО, когда X 1 = X 2 = X. Амплитуды интермодуляций (2n – 1) - го порядка с частотами
[n f 1 – (n – 1) f 2] для n > 1 описываются, согласно (2.6.6), выражением
В случае ИО при равноуровневом бигармоническом входном воздействии можно записать следующее равенство:
(2.6.21)
Обратим внимание на то, что в случае ИО при равноуровневом бигармоническом входном воздействии на выходе полосового фильтра со средней частотой f ср = (f 1 + f 2) / 2 и c полосой пропускания во много раз большей разности частот D f = f 1 – f 2, включенного после ИО, имеет место фазоманипулированный по закону меандра сигнал. Период манипуляции Т обусловлен разностью частот D f и равен Т = 1 / D f. Роль несущего колебания играет средняя частота f ср = (f 1 + f 2) / 2. Амплитуды спектральных составляющих фазоманипулированного сигнала Y n легко определяются [132]. Они равны
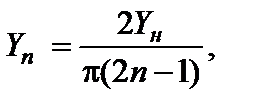(2.6.22)
где Y н – амплитуда несущего колебания.
Так как при гармоническом воздействии амплитуда основной гармоники колебания на выходе ИО равна Y 2 = 4 / p, то, принимая во внимание (2.6.22), выражение для амплитуд интермодуляционных (2n – 1) - го порядка на выходе ИО принимает окончательный вид:
(2.6.23)
С учетом (2.6.21) и (2.6.23) можно записать предельные значения рядов бесселевых функций:
при n > 1 и 0 < X < 1. (2.6.24)
Выражение для основных гармоник колебания при равноуровневом бигармоническом входном воздействии на УО имеет вид:
В случае ИО для основных гармоник будет иметь место следующее выражение:
(2.6.25)
С учетом (2.6.23) и (2.6.25) можно записать ряд для бесселевых функций:
(2.6.26)
Принимая во внимание тот факт, что на выходе ИО отсутствуют интермодуляции четного порядка, можно записать следующее равенство, обеспечивающее это условие в случае равноуровневого бигармонического входного воздействия:
для 0 < X < 1 и n + m = 2r. (2.6.27)
В общем случае полигармонического входного воздействия, когда общее число компонентов сигнала на входе ИО равноI, на его выходе также отсутствуют интермодуляции четных порядков. Поэтому можно записать следующее более общее выражение для ряда бесселевых функций:
для 
и 
(2.6.28)
Формула (2.6.27) является частным случаем (2.6.28) при X 1= X 2= X и X 3= X 4=….= X =0.
Таким образом, вышерассмотренные примеры показывают, что предложенная математическая модель УО, представляющая собой сумму линейной функции и ряда Фурье, предоставляет широкие возможности для решения различного рода
практически важных задач, связанных с нелинейными искажениями в УО, не только
в случае одиночных гармонических, как это делает традиционная кусочно-линейная модель УО, но и в случае сложных входных сигналов, содержащих большое число компонентов. Предложенный метод моделирования УО не накладывает ограничений ни на число воздействующих на вход УО гармонических колебаний, ни на порядок интермодуляционных составляющих спектра выходного колебания.
Некоторые из полученных выше пределов функциональных рядов (2.6.8), (2.6.9), (2.6.13), (2.6.18), (2.6.24), (2.6.26), (2.6.27) и (2.6.28), отсутствующие в общедоступной справочной литературе, возможно, могут быть полезными при решении другого рода задач, использующих аппарат функций Бесселя.
2.7. Общая аналитическая модель преобразователя частоты
Преобразователи частоты во многом обусловливают качество главных трактов приемных устройств [15, 148, 257, и др.], а, следовательно, и помехоустойчивость систем связи, поэтому при оптимизации структурных схем главных трактов приемников вопросам моделирования преобразователей частоты необходимо уделять особое внимание.
Преобразователи частоты являются сугубо нелинейными элементами, осуществляющими взаимодействие между поступающим с входа приемного устройства колебанием U 1(t) и колебанием гетеродина U г(t). Целью этого взаимодействия является перенос спектра частот входного колебания в другую часть диапазона. Выходное колебание преобразователя U 2(t) в общем виде можно представить как результат нелинейного взаимодействия суперпозиции колебаний U 1(t) и U г(t):
U 2(t) = F(U г(t) ± U 1(t)). (2.7.1)
В общем случае F(x) является функцией, содержащей четную и нечетную части:
F(x) = Fч(x) + Fн(х). (2.7.2)
Поэтому спектр выходного колебания U 2(t) при полигармонических входных воздействиях представляет собой совокупность отдельных комбинационных и
интермодуляционных составляющих четных и нечетных порядков. При преобразовании частоты полезным продуктом являются интермодуляционные составляющие второго, т. е. четного порядка. Поэтому в преобразователях частоты используются схемы, которые дают возможность компенсировать составляющие спектра нечетных порядков. Такого рода преобразователями, например, являются диодные смесители, собранные по балансной или кольцевой схемам.
Алгоритм балансного смесителя описывается выражением
U 2(t) = F1(U г(t) + U 1(t)) - F2(U г(t) - U 1(t)). (2.7.3)
С учетом (2.7.2), это уравнение можно переписать в виде
U 2(t) = Fч1(U г(t) + U 1(t)) - Fч2(U г(t) - U 1(t)) +
+Fн1(U г(t) + U 1(t)) - Fн2(U г(t) - U 1(t)). (2.7.4)
Алгоритм кольцевого смесителя можно описать выражением
U 2(t) = Fч1(U г(t) + U 1(t)) - Fч2(U г(t) - U 1(t)) +
+ Fн1(U г(t) + U 1(t)) - Fн2(U г(t) - U 1(t)) - (2.7.5)
- Fч3(U 1(t) - U г(t)) + Fч4(- U г(t) - U 1(t)) -
- Fн3(U 1(t) - U г(t)) + Fн4(- U г(t) - U 1(t)).
|
|
|
