 |
1) Основные свойства линейных блоковых кодов.
|
|
|
|
1) Основные свойства линейных блоковых кодов.
Наибольшее распространение среди блоковых (блочных) кодов получили равномерные линейные коды. Напомним основные свойства этих кодов.
Равномерные коды характеризуются постоянством длины 
кодового слова. Линейными являются все коды, для которых поразрядная сумма по модулю 
любой пары «разрешенных» (кодовых) слов дает кодовое слово.
Обозначим через 
произвольный 
-мерный вектор, соответствующий 
-му ( 
, где 
– мощность алфавита кода (для двоичного кода 
) ) кодовому слову. Приведем необходимые для дальнейшего рассмотрения определения.
Определения.
1. Весом Хэмминга 
вектора 
называется число ненулевых компонент этого вектора.
2. Минимальный вес кода есть минимальный вес ненулевого кодового слова.
Таким образом, если 
и 
– кодовые слова линейного кода, то вектор 
(сивол 
обозначает суммирование по модулю 
) также является кодовым словом. Следовательно, кодовое расстояние между двумя кодовыми словами равно весу порожденного ими третьего кодового слова и значит минимальное расстояние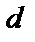 
для линейного кода равно минимальному весу 
его ненулевых кодовых слов и является минимальным весом кода.
Пример 1.
.
Рассмотренное выше важное свойство лежит в основе анализа исправляющей способности линейных блоковых кодов.
Известно множество оценок верхней и нижней границ минимального расстояния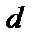 
для линейных блоковых кодов при фиксированной длине 
и относительной скорости 
. К их числу относятся верхние границы Плоткина и Синлгтона, граница Варшамова–Гилберта и другие [1, 4].
В качестве примера остановимся на анализе верхней границы Хэмминга параметра 
для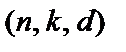 
-кода. Верхняя граница свидетельствует о том, что не существует кода, параметры которого лежат выше этой границы.
|
|
|
Граница Хэмминга указывает на наибольшее число кодовых слов ( 
), возможных при данной длине кода ( 
) и его исправляющей способности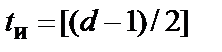 
( 
), или характеризует границу избыточности ( 
), необходимой при заданных значениях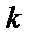 
и 
. Здесь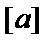 
обозначает целую часть 
. Обобщение этой границы для недвоичных кодов имеет вид
, (1)
где 
– мощность алфавита кодовых символов (для двоичных кодов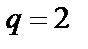 
);
– исправляющая способность кода, т. е. число, характеризующее максимальную кратность (длину пакета) исправляемых ошибок;
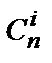– биномиальный коэффициент Ньютона вида 
(число сочетаний из 
по 
).
Границу Хэмминга (1) иногда называют «нижней» границей числа проверочных разрядов 
, определяющую необходимое число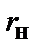 
проверочных разрядов для обеспечения требуемой исправляющей (обнаруживающей 
) способности кода. В этом смысле граница Варшамова-Гилберта вида
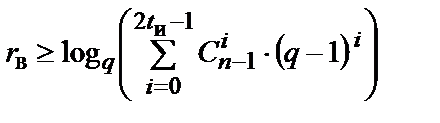, (1*)
может быть названа «верхней» границей и определяет достаточное для обеспечения требуемого ( 
) число 
проверочных разрядов.
Пример 2.
Размер кодовой комбинации 
дв. разряд. Необходимо определить «нижнюю» и «верхнюю» границу числа 
( 
и ) проверочных разрядов для обеспечения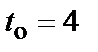 
-х кратной обнаруживающей способности кода, минимальное кодовое расстояние 
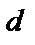кода, кратность 
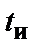исправляемых ошибок, и допустимое число 
информационных разрядов в обеих случаях.
Решение.
Известно, что минимальное кодовое расстояние равно 
и следовательно при 
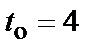исправляющая способность кода равна 
, а 
. Используя соотношение (1) получим
,
т. е. 
и значит 
дв. разрядов, а используя (1*) –
,
т. е. 
и значит 
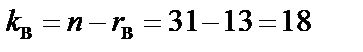дв. разрядов.
Таким образом конструктивные параметры кода можно записать в виде (31, 22, 5) и (31, 18, 5). Из полученного результата видно, что граница Хэмминга (1) в то же время является «верхней» с точки зрения числа возможных комбинаций информационных и следовательно кодовых слов –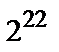 
.
|
|
|
Разрешающую способность линейных блоковых кодов проиллюстрируем на примере тривиального кода Хэмминга, состоящего из двух 3-мерных кодовых слов 
и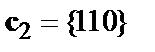 
.
На рис. 1 изображено множество всех возможных кодов длины 
(мощность этого множества равна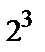 
) графически – в виде вершин куба.
При возникновении однократной ошибки в кодовом слове возможно появление следующих кодов: 
, 
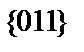и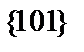 
; в слове 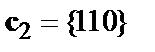– кодов: 
, 
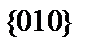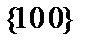и 
. Из рисунка видно, что «возврат» к соответствующему безошибочному кодовому слову от каждой ошибочной «тройки» кодов очевиден («путь» в один шаг показан стрелками). Другие возможные варианты «путей» (с использованием «пунктирных» граней), ведущие к альтернативному кодовому слову, увеличивают их на один шаг, что исключает их из рассмотрения.
| 1 1 0 |
| 1 0 0 |
| 1 1 1 |
| 1 0 1 |
| 0 0 1 |
| 0 1 1 |
| 0 1 0 |
| 0 0 0 |
| Рис. 1 |
Линейный блоковый код характеризуется такими показателями как упаковка и покрытие кода. Исправляющая способность кода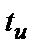 
является по сути «радиусом» упаковки кода. Покрытие кода – это область кодового пространства, в котором находится множество всех возможных кодов длины 
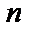. Оно характеризуется «радиусом» покрытия кода с центром в кодовом слове, равному такому кодовому расстоянию 
от кодовых слов до любых других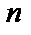 
-мерных кодов, при котором все такие коды оказываются в «сферах» радиуса .
Если «радиусы» упаковки и покрытия кода равны, код называется совершенным.
Так для кодов Хэмминга внутри «сферы радиуса» 
с центром в кодовом («разрешенном») слове находятся все принятые слова длины 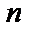, которые декодируются в это кодовое слово.
В рассмотренном выше примере внутри «сферы» с «радиусом»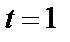 
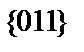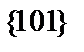с центром в слове находятся принятые слова , и , которые декодируются в случае одиночной ошибки в 
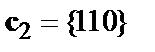, а в центре в слове – слова 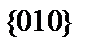, 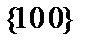и , которые декодируются в 
. Видно, что в сферах с радиусом упаковки кода оказались все возможные комбинации кодов в слове из 
двоичных разрядов, т. е. радиус покрытия равен радиусу упаковки кода из чего следует, что рассмотренный код совершенен.
|
|
|
Показано, что все коды Хэмминга примитивной длины ( 
, 
– число проверочных разрядов) совершенны.
|
|
|
