 |
Исследование области определения функции f(x).
|
|
|
|
ПРОГРАММИРОВАНИЕ В ЭЛЕКТРОННЫХ ТАБЛИЦАХ
Учебное пособие
по проектно‑ориентированному обучению
по дисциплине: «Информатика»
Екатеринбург
УДК 621.3
ББК
К
ПРОГРАММИРОВАНИЕ В ЭЛЕКТРОННЫХ ТАБЛИЦАХ. Учебное пособие по проектно‑ориентированному обучению по дисциплине: «Информатика», Э.П. Макаров,. Екатеринбург: УРФУ, 2012, 100 с.
ISBN
Библиогр. 2 назв. Рис.. Табл..
Учебное пособие включает дидактический материал в форме «проектов», по базовой дисциплине «Информатика», раздел «Программирование в электронных таблицах». Темы учебных проектов выбраны в соответствии с рабочей программой по дисциплине «Информатика».
Учебное пособие предназначено для студентов, которые проходят обучение по направлениям подготовки (квалификация бакалавр): 140100 «Теплоэнергетика и теплотехника»; 140400 «Электроэнергетика и электротехника»; 140800 «Ядерная физика и технологии».
УДК 621.3
ББК
ISBN © УрФУ, 2012
© Макаров Э. П. 2012
ПРОГРАММИРОВАНИЕ В ЭЛЕКТРОННЫХ ТАБЛИЦАХ
Введение
Метод проектов является одним из широко известных методов активного обучения. Суть метода проектов – стимулировать интерес студентов к определенным проблемам, предполагающим владение определенной суммой знаний, и решение этих проблем через проектную деятельность, В основе метода проектов лежит: развитие познавательных навыков студентов, критического и творческого мышления; умение самостоятельно конструировать свои знания, увидеть, сформулировать и решить задачу, ориентироваться в информационном пространстве.
Метод проектов как метод активного обучения в курсе «Информатика» – это способ дидактического достижения цели через детальную разработку алгоритма решения математической задачи в электронных таблицах, которая должна завершиться конкретным результатом. Решение задачи предусматривает необходимость интегрирования знаний из области информатики и математики в объеме базовых курсов. При этом учебные проблемы взяты из базового курса математики, знакомые и значимые для студента в его будущей профессиональной деятельности.
|
|
|
Содержательная часть проекта структурирована с указанием поэтапных результатов и форм их представления. Основными этапами активного обучения на основе метода проектов являются:
· обсуждение постановки задачи учебного проекта;
· обсуждение математических методов решения задач;
· структурирование проекта с выделением подзадач, подбор необходимых информационных материалов;
· разработка алгоритмов и электронных таблиц для решения задач;
· анализ полученных данных, корректировка и оформление конечных результатов;
· презентация проекта (творческий отчет, обсуждение в группе исполнителей подобных проектов).
По результатам выполнения учебных проектов необходимо представить отчет в виде файла на компакт-диске (см. Приложение).
Темы учебных проектов выбраны в соответствии с рабочей программой по дисциплине «Информатика» ООП ВПО по направлениям подготовки (квалификация бакалавр) см: 140100 «Теплоэнергетика и теплотехника»; 140400 «Электроэнергетика и электротехника»; 140800 «Ядерная физика и технологии».
1. Численное решение нелинейных уравнений.
2. Исследование нелинейных функций и построение их графиков.
3. Численное интегрирование
Задания для активного обучения
Тема 1. Численное решение нелинейных уравнений
Постановка задачи
Приближенное решение нелинейных уравнений с одним неизвестным вида f(x)=0 с применением численных итерационных методов является одной из тех задач, которые наиболее часто встречаются в практике инженера. В общем случае задача не разрешима, поскольку для нелинейных функций не существует выражения в виде формулы с конечным числом алгебраических действий или они достаточно громоздки (например, для алгебраических уравнений третьего порядка). В подобных задачах применяют численные методы приближенного решения заданного уравнения с любой наперед заданной точностью.
|
|
|
Задача решения уравнения вида
f(x)=0, (1)
где f(x) – некоторая функция от x, представляет собой задачу об отыскании корней функции ‑ значений x, которые обращают уравнение (1) в тождество.
В учебном пособии рассматривается отыскание приближенных значений действительных корней уравнения (1). Примем для исследования в данном проекте функцию f(x) вида
f(x)=ax3+bx2+cx+d, (2)
где коэффициенты заданы значениями: a =1; b =2; c =-3; d =-1.
Решение задачи распадается на два этапа:
1 Отделение корня – выделение отрезка [ a,b ], принадлежащего области определения функции f(x), на котором существует только один корень xk уравнения (1). Границы этого отрезка можно рассматривать как первое приближение искомого значения корня (левая граница с недостатком, правая – с избытком).
2 Уточнение найденного приближенного значения корня с любой заданной точностью e(eps), т.е. нахождение более узкого отрезка [ a1,b1 ], который содержится в отрезке [ a,b ] и также содержащий единственный корень xk.
Для отделения корней уравнения (1) нужно выполнить следующие действия
1 Исследовать критические точки (границы интервалов монотонности) функции f(x). Определить критические точки функции по формулам корней первой производной, аналитическим и табличным способами. Отобразить результаты исследования критических точек функции на диаграмме (графике функции).
2 Исследовать интервалы, где существует единственный корень функции. Отделить корни функции аналитическим и табличным способами. Отобразить результаты исследования на диаграмме (графике функции).
3 Произвести оценку погрешности найденного приближенного значения корня.
4 Исследовать эффективность способов отделения корня различными способами в электронных таблицах.
Для уточнения найденного приближенного значения корня уравнения (1) с любой заданной точностью eps нужно выполнить следующие действия.
|
|
|
1 Выбрать способ уточнения (табличный, графический, итерационный).
2 Произвести уточнение приближенного значения корня уравнения табличным и графическим способами.
3 Произвести уточнение итерационным методом.
4 Исследовать эффективность способов уточнения корня различными способами в электронных таблицах.
Исследование области определения функции f(x).
В проекте рассматриваются функции f(x), которые заданы аналитически (посредством формул) (Приложение 1). Исследование области определения функции и области ее изменения – это первый вопрос, на который надо ответить при исследовании функции.
Алгоритм 1.1. Исследование области определения функции f(x)
Функция y=f(x), в которой каждому значению x (независимой переменной) из множества X ставится в соответствие одно вполне определенное значение величины y (зависимой переменной), является определенной на множестве X. Множество X – это область естественного определения функции или область существования. Множество Y – множество всех значений, которые принимает при этом переменная y, называется областью изменений функции y= f(x).
Область существования функции определяется формулой, задающей функцию, а ее область определения задается условиями решаемой задачи, либо физическим смыслом изучаемого явления. То есть областью определения функции f(x) может быть любая часть области существования функции или они могут полностью совпадать.
Таким образом, когда говорят, что дана функция y=f(x), считают, что дана ее область определения X – она либо указано явно, либо ее надо предварительно найти с использованием математического анализа. Например, если по условию задачи нужно найти корень уравнения f(x)=0 на интервале [A,B], то область определения функции y=f(x) есть интервал [A,B].
Пример 1.1. Исследование области существования и определения функции y=f(x) вида (2)
Пусть дана f(x)=ax3+bx2+cx+d, где a,b,c,d – некоторые фиксированные числа, не равные нулю. Тогда каждому действительному числу a можно поставить в соответствие одно действительное число y = a a 3+b a 2+c a +d. То есть область существования функции y=ax3+bx2+cx+d – это множество всех действительных чисел [‑¥,+¥]. Если по условию задачи нужно найти корни уравнения f(x)=0, то область определения функции y=f(x) полностью совпадает с ее областью существования. Критические точки функции xk, которые являются корнями уравнения первой производной f(x)=0, делят область определения на интервалы монотонности. Для исследования функции y=f(x) область определения [‑¥,+¥] нужно сузить.
|
|
|
Исследование области существования и определения функции y=f(x) видов, которые даны в Приложении 1, приведено в Приложении 2.
2. Отделение корня функции f(x)
2.1. Исследование критических точек (границ интервалов монотонности) функции f(x) (формульным, аналитическим, табличными и графическим способами)
Алгоритм 2.1. Исследование критических точек функции f(x) по формулам корней первой производной функции
1. По данной y=f(x) определить формулы первой производной функции f1(x) и корней уравнения f1(x)=0.
2. Вычислить действительные корни уравнения первой производной функции f1(x)=0 (критические точки) по формулам.
3. Исследовать значения функции f(x) в критических точках.
4. Исследовать область определения функции f(x).
Пример 2.1. Исследование критических точек функции f(x) формульным способом.
Следуя инструкциям Алгоритма 2.1, выполнить следующие действия.
1. Определить выражения первой производной функции f(x) вида(2) и формулы для вычисления корней уравнения f1(x)=0. В ыражения для функции f(x) вида(2), ее первой производной f1(x) и второй производной f2(x), формулы для вычисления критических точек (корней  уравнения f1(x)=0)приведены в табл. 2.1.
уравнения f1(x)=0)приведены в табл. 2.1.
Таблица 2.1
| Характеристика | Выражение |
| Функция f(x) | f(x)=ax3+bx2+cx+d |
| Первая производная f1(x) | f1(x)= 3ax2+2bx+c |
| Критические точки (корни уравнения f1(x)=0) |  (3) (3)
|
| Вторая производная f2(x) | f2(x)= 3ax+b |
Ввести данные в ячейки электронной таблицы A2:D2 в соответствии с рис. 2.1.

Рис. 2.1. Электронная таблица вычисления значений корней уравнения f1(x)=0 и значений f(x) и f1(x) в критических точках
2. Ввести формулы для вычисления критических точек  в
в  в ячейки Е2 и Е3. Ввести формулы в ячейки F2 и G2 для вычисления значений функции f(x) и первой производной f1(x) в критической точке
в ячейки Е2 и Е3. Ввести формулы в ячейки F2 и G2 для вычисления значений функции f(x) и первой производной f1(x) в критической точке  по данным табл. 2.1 (3), скопировать формулы в ячейки F3 и G3. Выполнить вычисления (см. рис. 2.1).
по данным табл. 2.1 (3), скопировать формулы в ячейки F3 и G3. Выполнить вычисления (см. рис. 2.1).
3. Исследовать значения функции f(x) и первой производной f1(x) в критических точках(см. рис. 2.1). Область определения функции y=f1(x) полностью совпадает с областью определения y=f(x) (см. Пример 1.1).Значенияпервой производной в критических точках равны нулю. Значения функции f(x) при x=xk1 и при x=xk2 разные по знаку, что позволяет утверждать (на основании Теоремы 1, см. Алгоритм 2.2), что внутри интервала [ xk1, xk2] существует действительный корень уравнения f(x)=0.
|
|
|
4. Исследовать область определения функции f(x). Критические точки делят область определения функции f(x) на интервалы монотонности
[‑¥, xk1 ], [ xk1, xk2], [xk2+¥].
Определим знак функции f(x) на границах интервалов:
xk1=-1,869; xk2=0,535.
f( ‑¥ )<0; f(xk1)>0; f( xk2 )<0 f( +¥ )>0. (4)
5. Значения функции f(x) на границах интервалов монотонности разные по знаку, что позволяет утверждать (на основании Теоремы 1, см. Алгоритм 2.2), что внутри этих интервалов существуют действительные корни уравнения f(x)=0.
Для исследования функции y=f(x) область определения [‑¥,+¥] нужно сузить. Подберем значение левой границы первого интервала [‑¥, xk1 ], например, примем равной -4, а значение правой границы интервала [xk2+¥] примем равной 3. Проверим знак функции f(x) на границах интервалов: f(-4)<0; f(3)>0, что соответствует знакам функции f(x) на границах интервалов монотонности (4). Таким образом областью определения функции f(x) является суженный интервал [-4,3], который делится критическими точками на три интервала монотонности
[‑4, xk1 ], [ xk1, xk2 ], [ xk2, 3]. (5)
Алгоритм 2.2. Исследование критических точек функции f(x) аналитическим способом
Решение задачи распадается на два этапа:
Отделение критической точки – выделение интервала [ a,b ], принадлежащего области определения функции f1(x), на котором существует только одна критическая точка xk уравнения f1(x)=0. Границы этого интервала можно рассматривать как первое приближение искомого значения критической точки (левая граница с недостатком, правая – с избытком).
Уточнение найденного приближенного значения критической точки с любой заданной точностью e (eps), т.е. нахождение более узкого интервала [a1,b1], который содержится в интервале [a,b] и также содержащий единственную критическую точку xk.
Отделение критической точки функции f(x)
Для отделения корней функции f1(x) на интервале [ a,b ] аналитическим способом необходимо воспользоваться теоремой математического анализа «О существовании корня функции f(x)»
Теорема 1 «О существовании корня функции f(x)». Если функция f(x) непрерывна на интервале [ a,b ], а на концах интервала ее значения имеют разные знаки, то на этом интервале существует корень уравнения (1) (необходимое условие). Логическое условие, которое имеет значение ИСТИНА, когда необходимое условие выполняется, имеет вид
f(a)*f(b)<0 (6).
1. По данным таблицы ряда значений первой производной f1(x) выполнить ее исследование на границах интервалов значений x, заданных таблично.
2. Руководствуясь выводами теоремы 1, проверить выполнение необходимого условия существования корня (6) для уравнения первой производной f1(x)=0 с помощью логической функции ЕСЛИ(). Если логическое условие (7) имеет значение ИСТИНА, вывести текст «Критическая точка», иначе «Нет».
f1(a)*f1(b)<0. (7)
Пример 2.2. Отделение критических точеканалитическим способом.
Следуя инструкциям алгоритма 2.2, выполнить следующие действия.
1. Создать электронную таблицу вычисления ряда значений величины x на интервале [-4,3] по формуле арифметической прогрессии (xi+1 = xi + hx, где i =1,2,…15) (рис. 2.2). Ввести в ячейки: B3 значение -4 (минимальное значение x1); в D3 значение 0,5 (шаг hx). В ячейку А5 ввести формулу =B3, чтобы скопировать минимальное значение x1. Выделить диапазон А6:А19 и ввести в ячейку А6 формулу =А5+$D$3 для вычисления x2 (x2= x1+ hx) и выполнить копирование формулы в ячейке А5 на диапазон (удерживая клавишу <Ctrl> нажать клавишу<Enter>
2. Создать электронную таблицу вычисления ряда значений величины f(x)=ax3+bx2+cx+d. Выделить диапазон В5:В19, ввести в ячейку В5 формулу =$A$2*A5^3+$B$2*A5^2+$C$2*A5+$D$2 и выполнить копирование формулы в ячейке B5 на диапазон (см. рис. 2.2).
3. Создать электронную таблицу вычисления ряда значений величины f1(x)=3ax2+2bx+c. Выделить диапазон C5:C19, ввести в ячейку C5 формулу =3*$A$2*A5^2+2*$B$2*A5+$C$2 и выполнить копирование формулы в ячейке C5 на диапазон (см. рис. 2.2).

Рис. 2.2. Электронная таблица вычисления ряда значений величин f(x), f1(x), f2(x) и отделения критических точек
4. Создать электронную таблицу вычисления ряда значений величины f2(x)=3ax+b. Выделить диапазон D5:D19, ввести в ячейку D5 формулу =3*$A$2*A5+$B$2 и выполнить копирование формулы в ячейке D5 на диапазон (см. рис. 2.2).
5. Создать электронную таблицу проверки логического условия (7). Обратимся к рис. 2.2. Выделить диапазон E6:E19, ввести логическую формулу с функцией ЕСЛИ() для проверки логического условия и принятия решения о выполнении необходимого условия существования корня уравнения первой производной f1(x)=0 на интервале [ a,b ], которая имеет вид
=ЕСЛИ(С5*С6<0; «Критическая точка»; “Нет”).
Выполнить копирование формулы в ячейке Е6 на диапазон (см. рис. 2.2).
Анализ результатов проверки логического условия показывает, что на каждом из интервалов [ -2;-1,5 ], [ 0,5;1,0 ] выполняется необходимое условие существования корня уравнения f1(x)=0, т.е. на этих интервалах существуют критические точки. Полученные результаты соответствуют расчетным значениям по формулам xk1=-1,869; xk2=0,535 (см. (5), Пример 2.1), которые находятся внутри этих интервалов.
Уточнение критических точек функции f(x) табличным способом
Точность приближенного значения критической точки xk определяется длиной интервала [a,b], содержащего единственную критическую точку. Способ уточнения найденного приближенного значения критической точки xk с любой заданной точностью e (eps) состоит в нахождение более узкого интервала [a1,b1], который содержится в интервале [a,b] и также содержащего единственную критическую точку. На каждой итерации проверяется логические условия останова процесса уточнения корня (8).
Алгоритм 2.3. Уточнение критических точек функции f(x) табличным способом
1. По данным интервала [ a,b ], на котором существует единственная критическая точка ((см. (7), Алгоритм 2.2), вычислить ряд значений x: задать начальное значение ряда x=a и шаг по x, равный 0,1*(b-a). Для полученных значений ряда значений x вычислить ряд значений функции f1(x).
2. Исследовать значения первой производной f1(x) на границах [ a1,b1 ] интервала значений x, заданных таблично, аналитическим методом, проверив выполнение необходимого условия существования корня с помощью логической функции ЕСЛИ() (см. (7), Алгоритм 2.2). Отделить приближенное значение корня xki на i -й итерации (i=1,2,…) – определить интервал [ ai,bi ], содержащий критическую точку (уточнить критическую точку).
3. Исследовать достижение заданной точности eps оценки критической точки xki , на интервале [ ai,bi ], проверив логические условия останова процесса уточнения критической точки (см. п.2.??)
½ ai‑bi ½<eps. (8)
Если условия (8) выполняются (погрешность оценки не превышает заданную точность eps), то итерационный процесс уточнения критической точки xк функции f(x) на интервале [ a,b ] нужно закончить. За значение критической точки xк принимается значение xкi,полученное на последней i- й итерации.
4. Если условия не выполняются (погрешность оценки (8) превышает заданную точность eps), то итерационный процесс уточнения критической точки нужно продолжить, повторив пп.1-3 для интервала [ ai,bi ]. По данным интервала [ ai,bi ], на котором существует единственная критическая точка (см. п.2), вычислить ряд значений x для интервала [ ai,bi ]. Для этого в ячейках электронной таблицы, в которых на первой итерации были заданы начальное значение и шаг, нужно заменить начальное значение ряда x=ai и шаг по x, равный 0,1*(bi-ai). В результате замены будет выполнен автоматически пересчет рядов значений x и первой производной f1(x).
Пример 2.3. Уточнение приближенного значения критической точки табличным методом
Следуя инструкциям Алгоритма 2.3, выполнить следующие действия.
1. По данным интервала [ -2;-1,5 ], на котором существует единственная критическая точка (см. Пример 2.1), вычислить ряд значений x. В ячейках электронной таблицы Е38 и Е40 нужно задать начальное значение ряда x=-2 и шаг по x, равный 0,1*(-2;-1,5)=0,05, соответственно (см. рис. 2.3). Выделить ячейку А37 и ввести формулу =Е38 для копирования начального значения ряда. Выделить диапазон А38:А41 и ввести формулу =А37+$E$40 в ячейку А37 для вычисления ряда значений x по формуле арифметической прогрессии, которую скопировать на диапазон (<Ctrl+Enter>). Для полученных значений ряда значений x в диапазоне А38:А41 вычислить ряд значений первой производной f1(x) (рис. 3.1). Выделить диапазон В37:В41 и в ячейку В37 ввести или выполнить команды Копировать и Вставить с использованием «Специальная вставка» формулы для вычисления значения первой производной
==3*$A$2*A37^2+2*$B$2*A37+$C$2 (см. Пример 2.1). Скопировать формулу на диапазон В37:В41 (<Ctrl+Enter>).

Рис. 2.3. Электронная таблица табличного уточнения критической точки на интервале [-2;-1,5]
2. Исследовать значения первой производной f1(x) на границах [ a1,b1 ] интервала значений x, заданных таблично, аналитическим методом, проверив выполнение необходимого условия существования корня первой производной (7). Выделить диапазон С38:С41 и в ячейку С38 ввести формулу
=ЕСЛИ(В37*В38<0; “Критическая точка”;”Нет”),
которую размножить на диапазон (<Ctrl>+<Enter>). На первой итерации критическая точка отделена на интервале [ -1,9;-1,85 ] (см.рис.2.3).
3. Исследовать достижение заданной точности eps, значение которой (0,001) задано в ячейке Е41, оценки к критической точки xк, на интервале [ -1,9,-1,85 ], проверив логическое условие останова процесса уточнения корня (8). Выделить диапазон D38:D41 и в ячейку D38 ввести формулу
=ЕСЛИ(ABS(A38-A37)<E41; “Точность достигнута”;”Нет”), которую размножить на диапазон (<Ctrl>+<Enter>). Критическая точка, которая отделена на интервале [ -1,9,-1,85 ], не удовлетворяет требованиям заданной точности. Условие (8) не выполняется (погрешность оценки превышает заданную точность eps) и итерационный процесс уточнения критической точки нужно продолжить, повторив пп.1-3 для интервала [ -1,9;-1,85 ]. Для этого в ячейках электронной таблицы Е38 и Е40 нужно ввести новое начальное значение интервала (-1,9) и шага по x, равного 0,005, соответственно. В результате замены будет выполнен автоматически пересчет рядов значений x и производной f1(x).
4. Если условие (8) выполняется (погрешность оценки не превышает заданную точность eps), то итерационный процесс уточнения критической точки xк, функции f(x) на интервале [ -1,869;-1,868 ] нужно закончить. За значение критической точки xк принимается значение, равное одной изграниц интервала на последней итерации.
Алгоритм 2.4. Исследование критических точек функции f(x) графическим способом.
Геометрически необходимое условие существования корня функции f(x) на интервале [ a,b ] (Теорема 1) означает, что если концы дуги графика непрерывной функции f(x) находятся по разные стороны оси абсцисс Оx, то дуга пересекает ось Оx интервале [ a,b ] по крайней мере в одной точке x= xк.
1. Исследовать график производной f1(x) на границах интервалов значений x, заданных таблично, проверив геометрически выполнение необходимого условия существования корня первой производной. Если концы дуги графика производной f1(x) находятся по разные стороны оси абсцисс Оx, то дуга пересекает ось Оx наинтервале по крайней мере в одной точке x= xк. Провести анализ выполнения необходимого условия существования критической точки на этих интервалах.
2. Провести анализ эффективности отделения критической точки функции f(x) графическим способом. Исследовать график функции f(x) в окрестности критических точек.
Пример 2.4. Исследование критических точек функции f(x) графическим способом.
Следуя инструкциям алгоритма 2.4, выполните следующие действия.
1. Отобразить ряды значений x, f(x) и f1(x) на точечной диаграмме (см. рис. 2.2). Выделить диапазон А5:С19, содержащий значения базовых рядов «Ряд Х», «Ряд f(x)» и «Ряд f1(x)» для отображения на диаграмме. Выбрать на Ленте вкладку Вставить, далее в разделе Диаграммы выбрать тип диаграммы ‑ щелкнуть кнопку Точечная. В открывшемся меню выбрать подтип Точечной диаграммы – Точечна я с гладкими краями (рис.2.4).
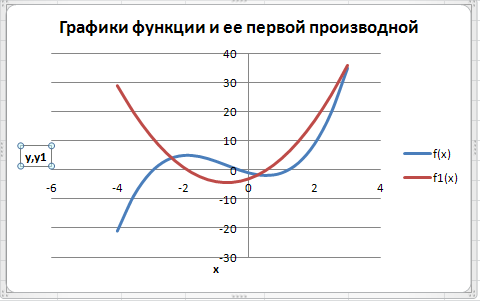
Рис. 2.4. Графики функции f(x) и ее первой производной
2. Выполнить форматирование оси Х на диаграмме. Вызвать диалоговое окно Формат оси, выделив ось Х на диаграмме, установив указатель мыши на оси и щелкнув правой кнопкой (рис. 2.5). В контекстном меню выбрать команду Формат оси. В диалоговом окне Формат оси на вкладке Параметры оси, которая открывается по умолчанию (рис. 2.6),установить значения в окнах: минимальное значение (по оси ОХ) фиксированное - -2,0; максимальное значение (по оси ОХ) фиксированное - -1,75; цена основных делений и цена промежуточных делений – фиксированные 0,05 и 0,01, соответственно.

Рис. 2.5. Контекстное меню для форматирования оси ОХ диаграммы

Рис. 2.6. Диалоговое окно с настройками оси ОХ для исследования критической точки функции на интервале [-2;-1,5]
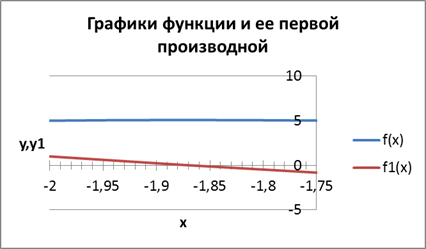
Рис. 2.7. Геометрическая интерпретация выполнения необходимого условия существования критической точки на интервале [-2;-1,75]
3. На графике первой производной функции f1(x) найти координаты критических точек функции f(x) и исследовать график функции f(x) в окрестности критических точек. Функция f(x) принимает экстремальные значения при значениях x=-1,8 и x=0,5, соответствующих нулям первой производной функции f1(x)=0 (значения определены по диаграмме приближенно).
2.2. Отделение корней функции f(x) аналитическим и табличным способами.
Алгоритм 2.5. Отделение корней функции f(x) аналитическим способом
Для отделения корней функции f(x) на интервале [ a,b ] аналитическим способом необходимо воспользоваться теоремами математического анализа «О существовании корня функции f(x)» (см. Теорема 1, Алгоритм 2.2) и «Об единственности корня функции».
Теорема 2. «Об единственности корня функции». Если функция f(x) непрерывна на интервале [ a,b ] и монотонна, а на концах интервала ее значения имеют разные знаки, то на этом интервале существует корень уравнения (1) и, причем единственный (достаточное условие). Логическое условие, которое имеет значение ИСТИНА, когда условие монотонности функции на интервале [ a,b ] выполняется, имеет вид
f1(a)*f1(b)> (9).
Логическое условие, в котором с помощью логической функции И() объединяются два логических условия (6) и (9) и которое имеет значение ИСТИНА, когда достаточное условие выполняется, имеет вид
И(f(a)*f(b)<0; f1(a)*f1(b)>0) (10).
1. Исследовать значения функции f(x) на границах интервалов значений x, заданных таблично, проверив выполнение необходимого условия существования корня (6) с помощью логической функции ЕСЛИ(). Если логическое условие (6) имеет значение ИСТИНА, вывести текст «Корень существует», иначе «Нет». Провести анализ результатов выполнения необходимого условия существования корня на этих интервалах.
2. Исследовать значения функции f(x) на границах интервалов значений x, заданных таблично, проверив выполнение условия монотонности функции (9) с помощью логической функции ЕСЛИ(). Если логическое условие (9) имеет значение ИСТИНА, вывести текст «Монотонна», иначе «Нет». Провести анализ результатов выполнения условия монотонности на этих интервалах.
3. Исследовать значения функции f(x) на границах интервалов значений x, заданных таблично, проверив выполнение достаточного условия существования корня (10) с помощью логической функции ЕСЛИ(). Если логическое условие (10) имеет значение ИСТИНА, вывести текст «Существует единственный корень», иначе «Нет». Провести анализ результатов выполнения достаточного условия существования корня на этих интервалах.
Пример 2.5. Отделение корней функции f(x) аналитическим способом.
Следуя инструкциям алгоритма 2.5, выполнить следующие действия.
1. Создать электронную таблицу проверки логического условия (6). Обратимся к рис. 2.8. Выделить диапазон F6:F19, ввести логическую формулу с функцией ЕСЛИ() для проверки логического условия и принятия решения о выполнении необходимого условия существования корня на интервале [ a,b ], которая имеет вид
=ЕСЛИ(B5*B6<0; “Корень существует”; “Нет”).
Выполнить копирование формулы в ячейке F6 на диапазон (рис. 2.8).
Анализ результатов проверки логического условия показывает, что на каждом из интервалов [ -3;-2,5 ], [ -0,5;0 ], [ 1;1,5 ] выполняется необходимое условие существования корня, т.е. на этих интервалах существует корень.
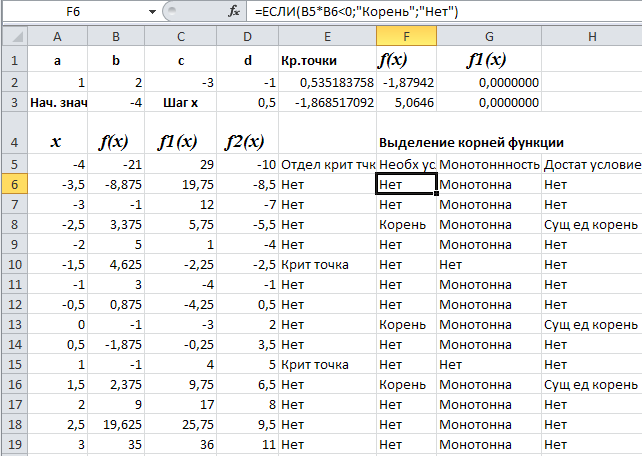
Рис. 2.8. Электронная таблица отделения корней f(x) аналитическим способом
2. Создать электронную таблицу проверки логического условия (9). Выделить диапазон G6:G19 (см. рис. 2.8), ввести логическую формулу с функцией ЕСЛИ() для проверки логического условия и принятия решения о выполнении условия монотонности функции на интервале [ a,b ], которая имеет вид
=ЕСЛИ(C5*C6>0; “Монотонна”; “Нет”).
Выполнить копирование формулы в ячейке G6 на диапазон (см. рис. 2.8).
Анализ результатов проверки логического условия показывает, что на каждом из интервалов, где выполняется необходимое условие существования корня (6), [ -3;-2,5 ], [ -0,5;0 ], [ 1;1,5 ] выполняется условие монотонности.
3. Создать электронную таблицу проверки логического условия (10). Выделить диапазон H6:H19 (см. рис. 2.8), ввести логическую формулу с функцией ЕСЛИ() для проверки логического условия и принятия решения о выполнении достаточного условия существования единственного корня функции на интервале [ a,b ], которая имеет вид
=ЕСЛИ(И(f(a)*f(b)<0; f1(a)*f1(b)>0); “Существует единственный корень”; “Нет”).
Выполнить копирование формулы в ячейке H6 на диапазон (см. рис.2.8).
Анализ результатов проверки логического условия показывает, что на каждом из интервалов [ -3;-2,5 ], [ -0,5;0 ], [ 1;1,5 ] выполняется достаточное условие существования корня и, причем единственного.
Алгоритм 2.6. Отделение корней функции f(x) графическим способом
Для отделения корней функции f(x) на интервале [ a,b ] графическим способом необходимо воспользоваться геометрической интерпретацией теорем математического анализа «О существовании корня функции f(x)» и «Об единственности корня функции» (см. Алгоритмы 2.2 и 2.5).
Геометрически необходимое условие существования корня функции f(x) на интервале [ a,b ] (Теорема 1) означает, что если концы дуги графика непрерывной функции f(x) находятся по разные стороны оси абсцисс Оx, то дуга пересекает ось Оx интервале [ a,b ] по крайней мере в одной точке x= xк (см. рис.2.4).
Геометрически условие монотонности функции f(x) на интервале [ a,b ] означает, что если концы дуги графика производной непрерывной функции f1(x) находятся по одну сторону от оси абсцисс Оx, то дуга f1(x) не пересекает ось Оx и можно утверждать, что функция f(x) монотоннана данном интервале [ a,b ] (см. рис.2.4).
Геометрически необходимое условие существования корня функции f(x) на интервале [ a,b ] (Теорема 2) означает, что если концы дуги графика непрерывной функции f(x) находятся по разные стороны оси абсцисс Оx, а концы дуги графика производной непрерывной функции f1(x) находятся по одну сторону от оси абсцисс Оx, то наинтервале [ a,b ] существует корень x=xк уравнения (1) и, причем единственный(см. рис.2.4).
1. Исследовать график функции f(x) на границах интервалов значений x, заданных таблично, проверив геометрически выполнение необходимого условия существования корня (6). Если концы дуги графика непрерывной функции f(x) находятся по разные стороны оси абсцисс Оx, то дуга пересекает ось Оx интервале по крайней мере в одной точке x= xк (см. рис.2.4). Провести анализ результатов выполнения необходимого условия существования корня на этих интервалах.
4. Исследовать значения функции f(x) на границах интервалов значений x, заданных таблично, проверив геометрически выполнение условия монотонности функции (9). Если концы дуги графика производной непрерывной функции f1(x) находятся по одну сторону от оси абсцисс Оx, то дуга f1(x) не пересекает ось Оx и можно утверждать, что функция f(x) монотоннана данном интервале (см. рис.2.4). Провести анализ результатов выполнения условия монотонности на этих интервалах.
5. Исследовать значения функции f(x) на границах интервалов значений x, заданных таблично, проверив выполнение достаточного условия существования корня (10). Если концы дуги графика непрерывной функции f(x) находятся по разные стороны оси абсцисс Оx, а концы дуги графика производной f1(x) находятся по одну сторону от оси абсцисс Оx, то наинтервале существует корень x=xк уравнения (1) и, причем единственный. Провести анализ результатов выполнения достаточного условия существования корня на этих интервалах.
6. Провести анализ эффективности отделения корней функции f(x) графическим способом.
Пример 2.6 Отделение корней функции f(x) графическим способом
Следуя инструкциям Алгоритма 2.6, выполнить следующие действия.
1. Создать внедренную точечную диаграмму для отображения рядов значений x, f(x), f1(x) (см. рис. 2.2 и 2.4).
2. Исследовать график функции f(x) на границах интервалов значений x, заданных таблично, проверив геометрически выполнение необходимого условия существования корня (6). Так как на концах интервала [ -3;-2,5 ] дуги графика непрерывной функции f(x) находятся по разные стороны оси абсцисс Оx и дуга пересекает ось Оx наинтервале в одной точке, то можно утверждать, что на этом интервале существует корень (см. рис.2.4). Анализ результатов проверки логического условия показывает, что на каждом из интервалов [ -3;-2,5 ], [ -0,5;0 ], [ 1;1,5 ] выполняется необходимое условие существования корня, т.е. на этих интервалах существует корень.
3. Исследовать значения функции f(x) на границах интервалов значений x, заданных таблично, проверив геометрически выполнение условия монотонности функции (9). Так как концы дуги графика производной непрерывной функции f1(x) на интервале [ -3;-2,5 ] находятся по одну сторону от оси абсцисс Оx, дуга f1(x) не пересекает ось Оx и можно утверждать, что функция f(x) монотоннана данном интервале (см. рис.2.4). Анализ результатов проверки логического условия (9) показывает, что на каждом из интервалов [ -3;-2,5 ], [ -0,5;0 ], [ 1;1,5 ] выполнения условия монотонности функции.
4. Исследовать график функции f(x) на границах интервалов значений x, заданных таблично, проверив геометрически выполнение достаточного условия существования корня (10). Так на концах интервала [ -3;-2,5 ] концы дуги графика непрерывной функции f(x) находятся по разные стороны оси абсцисс Оx, и концы дуги графика производной непрерывной функции f1(x) находятся по одну сторону от оси абсцисс Оx, то можно утверждать, что на интервале [ -3;-2,5 ] существует корень функция f(x) и, причем единственный (см. рис.2.4). Анализ результатов проверки логического условия показывает, что на каждом из интервалов [ -3;-2,5 ], [ -0,5;0 ], [ 1;1,5 ] выполняется достаточное условие су
|
|
|


