Механизм теплопроводности полимеров.

— С точки зрения физики твердого тела различают два механизма теплопроводности: электронный и фононный. Первый механизм реализуется в средах, содержащих металлы или другие носители свободных электронов. Второй механизм имеет место в диэлектриках.

— Рассмотрим, например, механизм переноса тепла в кубической кристаллической решетке поваренной соли. В узлах решетки располагаются ионы Na⁺ и Cl^–. Каждый из этих ионов осуществляет колебания около своего положения равновесия. При этом в пространстве между ионами происходит попеременное чередование зон сжатия и разряжения. Такое явление в физике носит название "звук". Эти ультразвуковые колебания распространяются в материале квантами, которые в отличие от электромагнитных квантов – фотонов называются фононами. Они характеризуются энергией E=hn (h – константа Планка, n – частота колебания).

— Для понимания процесса теплопроводности можно представить себе следующую модель. Пусть имеется ультразвуковой квант, в упрощенном варианте представляющий собой шар. Он перемещается внутри кристалла со скоростью звука. Представим себе некоторую энергетическую поверхность, имеющую потенциальную яму, характеризующую структурную неоднородность (например, ион К⁺ вместо Na⁺ или Br^– вместо Cl^–). Фононы "заскакивают" в эту яму, стремясь восполнить энергетическую неоднородность. Это явление в упрощенном варианте характеризует стадию прогрева материала. Если бы кристаллы не содержали дефектов, они прогревались бы мгновенно. После того, как вся яма заполнилась (наступил стационарный режим), перенос фононов уже не сопровождается нагревом. С помощью этой модели (при всей ее примитивности) можно пояснить физический смысл теплофизических характеристик (теплопроводности, температуропроводности и теплоемкости). Теплопроводность характеризуется скоростью перемещения носителей – фононов, то есть скоростью звука в материале. Теплоемкость характеризуется величиной потенциальной ямы и представляет собой способность тела аккумулировать тепло. И, наконец, температуропроводность, представляющая собой (по определению) отношение теплопроводности к объемной теплоемкости, характеризуется скоростью заполнения этой ямы. Чем больше скорость фононов, тем больше скорость заполнения ямы, чем больше сама яма, тем меньше скорость ее заполнения.

Вообще, толкование температуропроводности представляет нам хорошую возможность продемонстрировать ущербность метода, основанного на толковании физического смысла величины, исходя из ее размерности. Действительно, температуропроводность измеряется в м²/с. Хоть бы какой градус был, завалящий. В английском, французском, испанском языках эта величина называется коэффициентом тепловой диффузии. Такой термин более удачен, нежели коэффициент температуропроводности (такое название принято в немецком языке), потому что указывает на то, что тепловой поток не просто входит в образец с одной стороны и выходит – с другой, а диффундирует, пробивает себе дорогу. Но раз уж нам достался такой термин, давайте его осмыслим. Для этого запишем закон Фурье (кстати, он является следствием второго начала термодинамики):

,

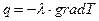где q – вектор теплового потока, gradT – вектор градиента температур, l – теплопроводность (тензор).

Если левую и правую часть этого выражения разделить на Сr (объемная теплоемкость), учитывая, что q/Cr=DT, l/Cr=a и dT=dDT, получим:

,

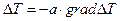где слева находится "поток" температуры, градиент которой находится справа, a – температуропроводность.

Таким образом, температуропроводность (как мера тепловой инерции) характеризует скорость распространения температуры, также как теплопроводность – скорость распространения тепла.

— Еще создатель теории теплопроводности Фурье указывал, что без знания теплофизических характеристик за теорией теплообмена остается лишь роль одного из разделов математической физики. Он имел в виду три рассмотренные нами выше характеристики.

— В связи с фононным механизмом переноса тепла теплопроводностью возникает необходимость ввести в рассмотрение в качестве тепловых характеристик акустические параметры. Среди них следует выделить скорость звука u (м/с); коэффициент поглощения a (1/м). В изотропном твердом теле в общем случае могут распространяться как сдвиговые, так и продольные волны.

— Скорость сдвиговых волн u_s выражается через модуль Юнга Е, модуль сдвига G, коэффициент Пуассона s и плотность r следующим образом:

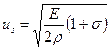
— Скорость продольных волн u_L выражается через аналогичные параметры и модуль объемной упругости В':

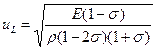
— Скоростьu и поглощениеa звука связаны с действительной и мнимой частью модуля эластичности (М):

,

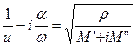где w – круговая частота.

При М'äM" (малое поглощение) можно получить:

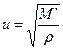
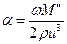
и далее эффективный модуль упругостиМ' (Па) при s @0.5 и эффективную вязкостьh' (Па×с):

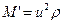
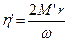
— При решении задач теплопроводности необходимо знать также интенсивность внутренних источников тепла q_v (Вт/м³) и суммарный тепловой эффект q_сум=òq_vdt (Дж/м³).

— Соотношение между теплопроводностью l и скоростью звука u дается уравнением Дебая-Киттеля:

,

где C – теплоемкость (Дж/(кг×К)); r – плотность (кг/м³); l – длина свободного пробега фонона (м); А – константа, равная ½ – ¼.

Понятие "длина свободного пробега фонона" нуждается в пояснении. Фонон, как квазичастица, при своем движении испытывает столкновения двоякого рода: столкновение типа фонон – фонон (динамическое искажение), приводящее к перераспределению энергии между фононами, и столкновение типа фонон – дефект (статическое искажение), приводящее к потере энергии фононом. Под длиной свободного пробега можно понимать расстояние от столкновения до столкновения, а можно понимать расстояние, на котором энергия фонона падает в е (основание натурального логарифма) раз. В последнем случае А принимается равной 0.33.

— Рассмотрим в качестве иллюстрации применения этого уравнения температурную зависимость теплопроводности кристаллического и аморфного твердого тела.

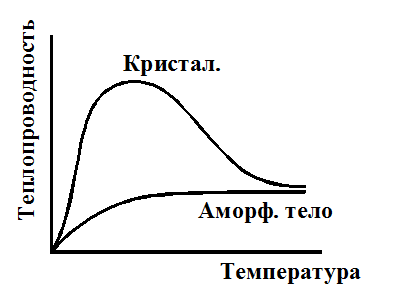При уменьшении температуры колебательное движение элементов структуры твердого кристаллического тела затормаживается. Поэтому длина свободного пробега фонона растет. Растет и теплопроводность. При определенной температуре (температура Дебая q) длина свободного пробега фонона становится равной размерам кристаллических образований, и перестает расти. При последующем понижении температуры теплопроводность начинает зависеть преимущественно от теплоемкости, которая равна нулю при Т=0К. Значение теплопроводности стремительно понижается при снижении температуры ниже q. Теплопроводность аморфных тел ведет себя при изменении температуры так же, как теплоемкость. С этой точки зрения аморфное тело – есть кристалл с малой длиной свободного пробега фонона. Другими словами, длина свободного пробега фонона в аморфном теле мала, равна размерам микрокристаллических образований и практически не зависит от температуры.