 |
Статистические оценки и проверка статистических гипотез.
|
|
|
|
— На практике исследователь всегда располагает лишь ограниченным числом значений измеряемой величины, представляющим собой некоторую выборку из генеральной совокупности. Под генеральной совокупностью понимают все допустимые значения случайной величины. Выборка называется репрезентативной (представительной), если она дает достаточное представление об особенностях генеральной совокупности. Оценки, получаемые по выборке, также являются случайными величинами. К ним предъявляются требования состоятельности и несмещенности. Оценка а& (Y1, Y2, …Ym) называется состоятельной, если с увеличением объема выборки m она стремится к оцениваемому параметру а. оценка называется несмещенной, если ее математическое ожидание при любом объеме выборки равно оцениваемому параметру M[a*]=a.
— Одной из статистических оценок является среднее арифметическое наблюдаемых величин. Пусть у нас имеется ряд наблюдений: Y1, Y2, …Ym. Необходимо охарактеризовать этот ряд каким-либо числом а.  Используем для этого метод наименьших квадратов:
Используем для этого метод наименьших квадратов:
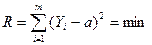 ; ;
|  ; ;
|   . .
|
Из этих выкладок явствует, что а – есть средняя арифметическая величина  , и это соответствует требованию метода наименьших квадратов.
, и это соответствует требованию метода наименьших квадратов.
— Характеристикой разброса наблюдений относительно среднего является выборочная дисперсия:
 ,
,
где m–1 представляет собой число степеней свободы n, обеспечивающее получение несмещенной оценки для дисперсии при малых выборках, при n>30 можно использовать n=n. Положительный квадратный корень из дисперсии представляет собой среднеквадратичное отклонение S. Коэффициент вариации (%):  .
.
— При проведении эксперимента реализуется серия процедур, объединяемых под общим названием: "Проверка статистических гипотез". Проверка гипотезы заключается в сопоставлении некоторых статистических показателей, критериев проверки (критериев значимости), вычисляемых по выборке, со значениями этих показателей, определенными в предположении, что проверяемая гипотеза верна. Чтобы принять или отвергнуть гипотезу, задаются уровнем значимости р. Наиболее употребительный уровень значимости 0.05 (5 %). Уровню значимости соответствует доверительная вероятность b=1–р.
|
|
|
— Доверительные 95 %-е интервалы для генерального среднего m:
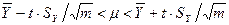 ,
,
критерий Стьюдента t выбирается из таблиц при числе степеней свободы n=m–1 и уровне значимости a =5%.
— Нижний и верхний пределы для дисперсии  :
:
 ,
,
критерий хи-квадрат (c2) выбирается при числе степеней свободы n=m-1 и уровне значимости a =95% – для нижнего предела и уровне значимости a =5% – для верхнего предела.
— Необходимое число наблюденийm0. Ориентировочный расчет:
m 0 =V2×t2/T2,
V – коэффициент вариации, %, t – показатель достоверности (критерий Стьюдента) выбирается при числе степеней свободы n=¥, Т – показатель точности (относительная ошибка), %.
— Проверка однородности результатов параллельных опытов по критерию Q. Данные располагаются в порядке возрастания или убывания (Y1, Y2,…Ym-1, Ym) так, чтобы сомнительный результат Ym оказался последним. После этого вычисляется критерий Q. Подозрительный результат может быть исключен, если
 .
.
Выражение в знаменателе – размах. Qкр выбирается при числе степеней свободы n=m.
— Попарное сравнение дисперсий по критерию Фишера F=  .
.
При одинаковом числе степеней свободы для каждой из n дисперсий находят отношение максимальной дисперсии к минимальной. Если эти дисперсии однородны, то будут однородны и все остальные. Полученное значение F-критерия сравнивается с критическим при числе степеней свободы для числителя mmax–1 и для знаменателя mmin–1 при уровне значимости 5 %. Если F<Fкр, гипотеза однородности дисперсии может быть принята.
|
|
|
— При n1=n2=... =nn=no целесообразно использовать критерий Кохрена, формирующийся как отношение максимальной дисперсии к сумме всех дисперсий:
G = S2max /  Sj2.
Sj2.
Если найденное по выборочным дисперсиям значение критерия Кохрена окажется меньше табличного G<Gтабл при числе степеней свободы m-1 для числителя и n – для знаменателя, расхождение между дисперсиями нужно считать случайным.
— Сравнение двух средних. Для сравнения двух средних можно использовать критерий Стьюдента: t=|y1ср–y2ср|×((m1×m2)/((m1+m2)×  ))0. 5,
))0. 5,  – средняя из двух дисперсий. Если t>tкр ., то можно считать, что два средних различаются с учетом ошибки опыта. Критическое значение критерия Стьюдента выбирается при числе степеней свободы n=m1+m2–2 и уровне значимости 5 %.
– средняя из двух дисперсий. Если t>tкр ., то можно считать, что два средних различаются с учетом ошибки опыта. Критическое значение критерия Стьюдента выбирается при числе степеней свободы n=m1+m2–2 и уровне значимости 5 %.
Планирование эксперимента.
— Под планированием эксперимента понимают область математической статистики, ставящую своей целью выбор количества и условий постановки экспериментов, необходимых и достаточных для решения задачи с требуемой точностью, разработку методов и приемов математической обработки экспериментальных результатов и принятия на основе этого определенных решений.
— Существует две разновидности эксперимента: пассивный и активный эксперимент. В рамках пассивного эксперимента уровни варьирования рецептурно-технологических факторов являются случайными, они соответствуют аппаратурным, временным, финансовым возможностям экспериментатора. В случае активного эксперимента переменные в эксперименте фиксируются на определенных уровнях и поддерживаются на них необходимое время. Конечно, активный эксперимент более эффективен с точки зрения достижения цели, но он не всегда может быть реализован.
3.3.1. Линейные планы.
— В зависимости от числа степеней свободы n=N–p (N – количество точек в плане, p – число коэффициентов модели) экспериментальные планы делятся на три категории. Ненасыщенные планы (n>0; N>p), в которых число экспериментальных точек (каждая точка отвечает определенному сочетанию уровней факторов) больше количества коэффициентов модели. В этом случае есть возможность вычислить коэффициенты модели и проверить ее адекватность. Насыщенные планы (n=0; N=p), в которых число экспериментальных точек равно количеству коэффициентов модели. В этой ситуации можно рассчитать параметры модели, но для проверки ее адекватности необходимо проведение дополнительных экспериментальных измерений в точках, координаты которых в ряде случаев не могут быть выбраны произвольно. Ненасыщенные планы (n<0; N<p), в которых число экспериментальных точек меньше количества коэффициентов модели. В этом случае построение параметрической модели не может быть осуществлено. Такие планы используются для выделения существенных переменных из множества факторов.
|
|
|
— Полный факторный эксперимент (ПФЭ) представляет собой эксперимент, включающий все возможные уровни факторов при выбранном их числе. В случае линейных планов он используется как экспериментально-статистический метод выделения существенных переменных. Рассмотрим ПФЭ 22. Здесь основание (2) – количество уровней каждого фактора, а показатель степени (2) – количество факторов. Y=b0+b1×X1+b2×X2 – модель без эффекта взаимодействия; Y=b0+b1×X1+b2×X2+b12×X1×X2 – модель с эффектом взаимодействия.
Организация эксперимента и проведение расчетов реализуются в следующей последовательности:
1. Выбор уровней варьирования факторов Z1 и Z2.
2. Преобразование значений уровней варьирования переменных Z1 и Z2 в условный масштабХ1 и Х2: Xj=(Zj–Zj0)/Az, где –1£Xj£+1; Zj0 – натуральное значение основного уровня, Az – интервал варьирования (в натуральном масштабе); Az = (Zjmax–Zjmin)/2; j - номер фактора.
3. Построение плана эксперимента и матрицы планирования:
| План: | Матрицы планирования: | |||||
| № | X1 | X2 | Код | Первая модель
 
| Вторая модель
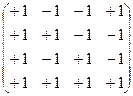
| |
| –1 | –1 | (1) | ||||
| +1 | –1 | a | ||||
| –1 | +1 | b | ||||
| +1 | +1 | ab | ||||
4. Вычисление коэффициентов линейных моделей:
| b0=SY/N=(Y1+Y2+Y3+Y4)/N b1=SX1×Y/N=(-Y1+Y2-Y3+Y4)/N | b2=SX2×Y/N=(-Y1-Y2+Y3+Y4)/N b12=SX1×X2×Y/N=(Y1-Y2-Y3+Y4)/N |
5. Вычисление дисперсии воспроизводимости по m измерениям в центре плана:
S2восп= 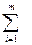 (Y0i-Y0ср)2 / (m-1) (Y0i-Y0ср)2 / (m-1)
| Y0ср = 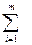 Y0i / m Y0i / m
|
6. Проверка значимости коэффициентов моделей осуществляется по критерию Стьюдента: t=|bi|/Sbi; bi – коэффициент, Sbi – корень квадратный из дисперсии определения этого коэффициента; S2bi=S2восп/N. Если рассчитанное значение t -критерия больше табличного при числе степеней свободы n = m-1 и уровне значимости a, то можно считать значимым рассматриваемый коэффициент; в противном случае может ставиться вопрос об исключении этого коэффициента из модели.
|
|
|
7. Проверка содержательности первой модели (для нее количество точек плана N больше количества коэффициентов р) проводится по критерию Фишера: F=S2R0/S2R.
Здесь S2R0=  (Yu–Yuср)2/(N–1); (Yu–Yuср)2/(N–1);
| S2R=  (Yu–Yuрасч)2/(N–p); (Yu–Yuрасч)2/(N–p);
| Yuср=  Yu/N. Yu/N.
|
Yu – экспериментальное значение, Yuрасч – рассчитанное значение, Yuср – среднее из точек плана.
Содержательность модели можно считать удовлетворительной, если дисперсия относительно среднего S2R0 значительно (не менее чем в 3-5 раз) превосходит величину остаточной дисперсии S2R.
8. Проверку адекватности модели также можно осуществить по критерию Фишера: F=S2R/S2восп=( (Yu–Yuрасч)2/(N–p))//(
(Yu–Yuрасч)2/(N–p))//(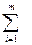 (Y0i–Y0ср)2/(m–1))
(Y0i–Y0ср)2/(m–1))
Рассчитанное значение критерия Фишера следует сравнить с табличным при числе степеней свободы n1=N-p и n2=m-1 (a =0,05). Условие адекватности модели Fрасч < Fтабл.
9. Проверка предсказательной способности в центре плана:
Эта проверка заключается в сопоставлении на основе критерия Стьюдента t=|b0-Y0ср|/(S2восп/m)0. 5. коэффициента b0 со средним значением отклика в центре плана. Рассчитанное значение критерия сравнивают с табличным при числе степеней свободы n=m-1. Предсказание в центре плана удовлетворительно при tрасч<tтабл.
— Аналогичным образом строятся ПФЭ 23, 24 и т.д.
— Дробная реплика является частью полного факторного эксперимента и служит для решения тех же задач, что и полный факторный эксперимент, но делает это более эффективно.
— Рассмотрим ПФЭ 23.
| План: | Матрица планирования: | ||||
| № | X1 | X2 | X3 | Код | 
|
| –1 | –1 | –1 | (1) | ||
| +1 | –1 | –1 | a | ||
| –1 | +1 | –1 | b | ||
| +1 | +1 | –1 | ab | ||
| –1 | –1 | +1 | c | ||
| +1 | –1 | +1 | ac | ||
| –1 | +1 | +1 | bc | ||
| +1 | +1 | +1 | abc |
С помощью этого плана можно построить модель без эффектов взаимодействия: Y=b0+b1×X1+b2×X2+b3×X3 для трех факторов. Число степеней свободы для этого плана N–p =9–4=4. Количество экспериментальных точек может быть сокращено в два раза путем использования половины ПФЭ. Как выбрать эти 4 точки из 8? Понятно, что их выбор не может быть произвольным. Восемь точек плана в пространстве образуют куб. при выборе четырех точек нужно взять по две точки с правой и левой грани, верхней и нижней, передней и задней. Этому требованию отвечают две полуреплики:

| 
|
— В каждой из этих полуреплик 23–1 первый столбец как бы "отвечает" за коэффициент b0, второй, третий и четвертый столбцы фактически представляют собой координаты четырех точек (в условном масштабе) и "отвечают" за коэффициенты b1, b2 и b3. Нетрудно заметить, что четвертый столбец во второй полуреплике равен произведению элементов второго и третьего, а в первой полуреплике тому же произведению, но с обратным знаком. Это обстоятельство может быть выражено соотношениями X3=X1×X2 и X3=–X1×X2, которые называются г енерирующими соотношениями.
|
|
|
— Если бы мы реализовали ПФЭ 23, то смогли бы построить полную модель Y=b0+b1×X1+b2×X2+b3×X3+b12×X1×X2+b13×X1×X3+b23×X2×X3+b123×X1×X2×X3 с эффектами взаимодействия. Мы строим модель без этих эффектов, предполагая, что их влияние незначительно. Фактически это сводится к тому, что каждый из рассчитываемых в этом случае линейных коэффициентов определяется вместе с каким-то из эффектов взаимодействия. Для определения системы смешивания необходимо сформировать определяющий контраст. Для этого, например, генерирующее соотношение X3=X1×X2 слева и справа умножим на Х3. Поскольку Х3. равен либо –1, либо +1, то  . Определяющий контраст имеет вид: 1=X1×X2×X3. Для определения системы смешивания умножаем левую и правую часть определяющего контраста на X1, затем на X2 и, наконец, на X3. Получим:
. Определяющий контраст имеет вид: 1=X1×X2×X3. Для определения системы смешивания умножаем левую и правую часть определяющего контраста на X1, затем на X2 и, наконец, на X3. Получим:  . Следовательно, мы определяем b1 совместно с b23 (b1®b1+b23), b2 – совместно с b13 (b2®b2+b13) и b3 – совместно с b12 (b3®b3+b12). И, наконец, b0 – совместно с b123.
. Следовательно, мы определяем b1 совместно с b23 (b1®b1+b23), b2 – совместно с b13 (b2®b2+b13) и b3 – совместно с b12 (b3®b3+b12). И, наконец, b0 – совместно с b123.
 |
— Аналогичным образом строится, например, дробная реплика 27–4. Вот ее кодированное изображение: def; afg; beg; abd; cdg; ace; bcf; abcdefg. За каждым фактором закреплены буквы латинского алфавита: Х1 – a; Х2 – b; Х3 – c; Х4 – d; Х5 – e Х6 – f; Х7 – g. Если в сроке матрицы (а строка – это координата точки) стоит буква, это значит, что соответствующий фактор находится на уровне +1, т.е. максимальном. Так, def означает, что максимальное значение имеют четвертый, пятый и шестой факторы, остальные – минимальное.
Планы второго порядка.
Для построения полинома второй степени, имеющего вид: 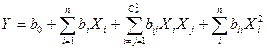 , в случае двух факторов, например, к точкам, образующим ядро плана и необходимым для построения линейной модели, добавляются еще точки, лежащие на осях координат ("звездные" точки), и точки в центре плана.
, в случае двух факторов, например, к точкам, образующим ядро плана и необходимым для построения линейной модели, добавляются еще точки, лежащие на осях координат ("звездные" точки), и точки в центре плана.
Общее количество точек N=nc+na+n0 (nc – количество точек, формирующих ядро плана, na – количество "звездных" точек, n0 – количество точек в центре плана). Эти три множества точек как бы образуют три сферы. Свойства плана зависят от величины "звездного" плеча и от количества экспериментов в центре плана.
Например, Если "звездное" плечо равно 1 (ПФЭ 32) будет получен ортогональный план, характеризующийся тем, что коэффициенты модели в этом случае определяются независимо друг от друга. В случае, когда "звездное" плечо (координата "звездной" точки) равно 1.414 и при n0 =5 получается ротатабельный план (в случае двух факторов), Этот план характеризуется тем, что дисперсия предсказания Y одинакова на одинаковых расстояниях от центра плана.
— Для построения моделей с двумя независимыми переменными удобно использовать программу Table Curve 3D. Эта программа дает возможность построить целый ряд моделей второго и третьего порядка, представляющих собой отрезки ряда Тейлора. Вот эти модели:
301. z=a+bx+cy+dx2+ey2+fxy
302. z=a+blnx+cy+d(lnx)2+ey2+fylnx
303. z=a+b/x+cy+d/x2+ey2+fy/x
304. z=a+bx+clny+dx2+e(lny)2+fxlny
305. z=a+blnx+clny+d(lnx)2+e(lny)2+flnxlny
306. z=a+b/x+clny+d/x2+e(lny)2+f(lny)/x
307. z=a+bx+c/y+dx2+e/y2+fx/y
308. z=a+blnx+c/y+d(lnx)2+e/y2+f(lnx)/y
309. z=a+b/x+c/y+d/x2+e/y2+f/(xy)
310. z=a+bx+cy+dx2+ey2+fxy+gx3+hy3+ixy2+jx2y
311. z=a+blnx+cy+d(lnx)2+ey2+fylnx+g(lnx)3+hy3+iy2lnx+jy(lnx)2
312. z=a+b/x+cy+d/x2+ey2+fy/x+g/x3+hy3+iy2/x+jy/x2
313. z=a+bx+clny+dx2+e(lny)2+fxlny+gx3+h(lny)3+ix(lny)2+jx2lny
314. z=a+blnx+clny+d(lnx)2+e(lny)2+flnxlny+g(lnx)3+h(lny)3+ilnx(lny)2+j(lnx)2lny
315. z=a+b/x+clny+d/x2+e(lny)2+f(lny)/x+g/x3+h(lny)3+i(lny)2/x+j(lny)/x2
316. z=a+bx+c/y+dx2+e/y2+fx/y+gx3+h/y3+ix/y2+jx2/y
317. z=a+blnx+c/y+d(lnx)2+e/y2+f(lnx)/y+g(lnx)3+h/y3+i(lnx)/y2+j(lnx)2/y
318. z=a+b/x+c/y+d/x2+e/y2+f/(xy)+g/x3+h/y3+i/(xy2)+j/(x2y)
— Программа позволяет сформировать различные варианты оформления пространственного изображения получаемой поверхности Z=f(X,Y), обеспечить качественное изображением с использованием специальных символов, подстрочных и надстрочных индексов и пр., показать на графике доверительные интервалы для отклика, дать отдельный график невязок в каждой точке плана, представляет листинг всех полученных моделей, дает результаты вычисления параметров, характеризующих качество модели (значимость коэффициентов, коэффициент детерминации, стандартная ошибка, критерий Фишера), выдает данные сравнения экспериментальных и рассчитанных значений отклика и доверительные интервалы, позволяет графически представить изменение производной отклика по каждому из факторов, позволяет рассмотреть поверхность в режиме анимации и многое другое.
Пример пространственного изображения представлен графически. Здесь же показаны линии равного уровня. К сожалению, программа не позволяеи определить, какому уровню отклика соответствует та или иная линия. Поэтому
 |
целесообразно получить уравнение в программе Table Curve 3D, а затем построить семейство изолиний в программе MatLab/
|
|
|


