 |
Раздел 6. Определённый интеграл.
|
|
|
|
6.1. Определённый интеграл: основные понятия, определения, свойства.
Пусть на отрезке 
задана непрерывная функция 
.
Фигура, ограниченная графиком функции 
, прямыми линиями, 
называется криволинейной трапецией. Найдём площадь 
этой трапеции.
Разобьём отрезок 
на 
произвольных частей точками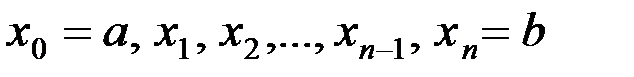 
. В каждом частичном отрезке 
длиной 
выберем произвольную точку 
. Построим прямоугольники с основанием 
и высотой 
.
Площадь полученной ступенчатой фигуры 
равна сумме площадей этих прямоугольников.
.
Сумма 
называется интегральной суммой, её значение приближённо равна площади криволинейной трапеции
.
С уменьшением всех величин точность приближения криволинейной трапеции ступенчатой фигурой и точность полученной формулы увеличиваются. Поэтому за точное значение площади 
криволинейной трапеции принимается предел, к которому стремится площадь ступенчатой фигуры 
, когда 
неограниченно возрастает 
или, что тоже самое, когда max 
, т.е.
.
Определение. Предел интегральной суммы 
при 
называется определённым интегралом от функции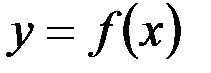 
и обозначается 
, т.е.
.
- нижний предел интегрирования,
- верхний предел интегрирования,
- подынтегральная функция,
- подынтегральное выражение;
- отрезок интегрирования.
Из определения определённого интеграла вытекает его геометрический смысл: определённый интеграл от неотрицательной функции численно равен площади криволинейной трапеции.
Определение. Ф ункция 
, для которой на отрезке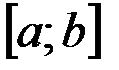 
существует определённый интеграл 
, называется интегрируемой на этом отрезке.
Теорема ( достаточное условие существования определённого интеграла ). Если функция 
непрерывна на отрезке 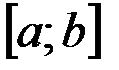, то существует определённый интеграл 
.
|
|
|
Свойства определённого интеграла.
Определённый интеграл от алгебраической суммы конечного числа функций равен алгебраической сумме определённых интегралов от каждого слагаемого.
.
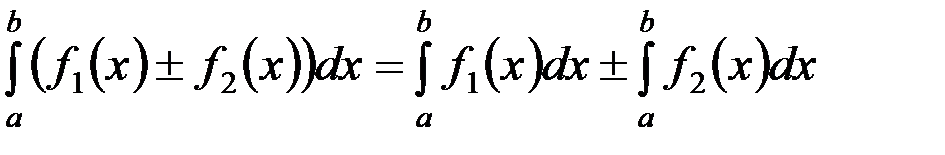Постоянный множитель можно выносить за знак определённого интеграла.
.
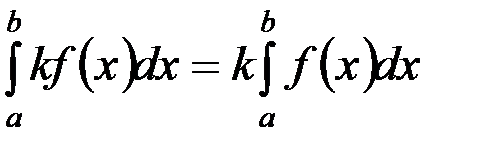При перестановке местами пределов интегрирования определённый интеграл меняет свой знак на противоположный.
.
Определённый интеграл с одинаковыми пределами равен нулю.
.
Отрезок интегрирования можно разбивать на части.
,
где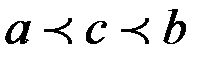 
.
Формула Ньютона - Лейбница. Основные методы вычисления определённого интеграла.
Вычисляют определённый интеграл 
по формуле Ньютона - Лейбница:
,
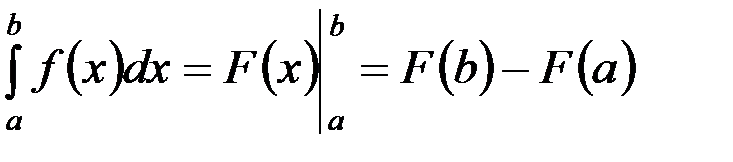где 
- первообразная для функции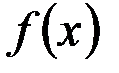 
.
Формула Ньютона - Лейбница применяется для вычисления определённого интеграла во всех случаях, когда может быть найдена первообразная функция 
для подынтегральной функции 
.
Для вычисления определённого интеграла от функции по формуле Ньютона - Лейбница необходимо сначала найти первообразную , поэтому для вычисления определённого интеграла применяют те же приёмы, что и для нахождения неопределённого интеграла.
Непосредственное интегрирование.
Пример 1. Вычислить определённый интеграл 
.
Решение. Применяя свойство 2 определённого интеграла, табличный интеграл 1 и формулу Ньютона - Лейбница, имеем:
.
Пример 2. Вычислить 
.
Решение. Последовательно применим свойства 1 и 2 определённого интеграла, табличный интеграл и формулу Ньютона - Лейбница, получим:
Пример 3. Вычислить 
.
Решение. Преобразуем подынтегральную функцию, разделив почленно числитель на знаменатель, применим свойство определённого интеграла 1 и табличные интегралы, получим
+ 
.
Пример 4. Вычислить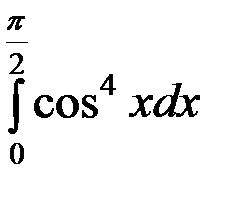 
.
Решение. Преобразуем подынтегральную функцию, дважды воспользовавшись тригонометрической формулой понижения степени:
|
|
|
= 
.
Получим
+ 
+ 
.
Геометрические приложения определенного интеграла.
|
|
|
