Метод множителей Лагранжа.

Задача на условный экстремум ставится как задача определения управляемых параметров

(8) (9)

, на которых достигается экстремум (максимум или минимум) при ограничениях, заданных уравнениями.

 

Задачу на условный экстремум можно свести к задаче на безусловный экстремум для специальным образом построенной функции.

Каждому ограничению поставим в соответствие переменную .

 

Построим функцию Лагранжа:

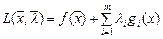
Если ограничения выполняются , то функция Лагранжа при любых λ превращается в исходную функцию.

Точки локальных экстремумов задачи (8), (9) будут точками локальных экстремумов функции Лагранжа.

Теорема 6 (необходимое условие экстремума): если 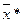– точка локального экстремума и в окрестности этой точки функции непрерывно дифференцируемы, то в этой точке выполняются условия

(10)

Условия (10) означают, что градиент функции Лагранжа равен нулю

(10’)

Для формулировки достаточных условий оптимальности рассмотрим

окаймляющую матрицу Гессе:

Теорема 7 (достаточное условие экстремума):

· Стационарная точка функции Лагранжа 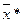является точкой локального минимума, если в окаймляющей матрице Гессе, вычисленной в стационарной точке, все угловые миноры, начиная с порядка имеют знаки, определяемые множителем .

· Стационарная точка функции Лагранжа 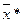является точкой локального максимума, если все угловые миноры окаймляющей матрицы Гессе, начиная с порядка образуют знакопеременный ряд, в котором знак первого члена определяется множителем .

 

Достаточное условие оптимальности можно сформулировать также в другой форме: если рассмотреть определитель, построенный из окаймляющей матрицы Гессе

(11)

,

то стационарная точка функции Лагранжа является точкой максимума, если все действительных корней многочлена (11) меньше ноля. Если же корни больше нуля, стационарная точка функции Лагранжа является точкой минимума.

Пример: Решим предыдущую задачу по определению плана производства, обеспечивающий наибольший доход методом Лагранжа.

Решение.

Задача сводится к нахождению максимума функции с ограничениями, где

(*.1)

с ограничением

(*.2)

 

Для приведения задачи оптимизации к стандартному виду введем функцию .

(*.3)

Преобразуем целевую функцию

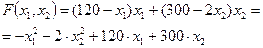
(*.4)

Построим функцию Лагранжа

	(*.5)

 

 

Вычислим частные производные функции Лагранжа

	(*.6)

 

Приравняем частные производные функции Лагранжа к нулю, в результате получим систему для нахождения , и .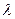

	(*.7)

 

Вычитая из второго уравнения первое, получим

	(*.8)

С учетом полученного результата систему можно преобразовать к следующему виду и решить её.

	(*.9)

 

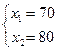
Далее определяем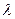

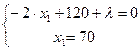
	(*.10)

Вычислим значение ЦФ в оптимальной точке

(*.11)

 

 

Для проверки достаточного условия оптимальности вычислим матрицу Гессе

 

	(*.12)

Пользуясь соотношениями (*.3) - (*.6)

 

 

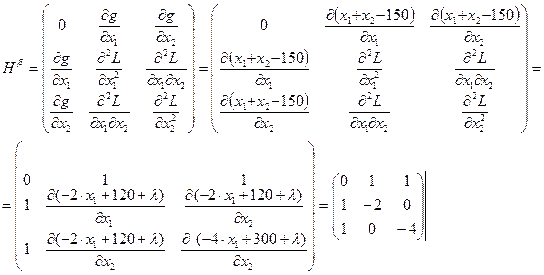
	(*.13)

 

 

Угловые миноры матрицы, начиная с порядка 2 m +1=3 должны иметь чередующиеся знаки, знак первого из них (положителен). Все эти условия выполняются:

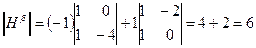
Полученное решение – точка локального максимума.

 

На рис.э.2 приведена схема задачи, иллюстрирующая полученное решение. На ней нанесена точка С, координаты которой и соответствуют оптимальному решению. Эта точка является точкой касания линии уровня (эллипса), соответствующего уровню (), и лини АВ, определяемой ограничением . Заметим, что в точке касания градиенты целевой функции и ограничения коллинеарны (параллельны).

Рис.(э.2).

 

⇐ Предыдущая1234Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: