П.3. Оптимальность по Нейману-Моргенштерну

Основу принципа Неймана-Моргенштерна (напомним, что Джон фон Нейман и Оскар Моргенштерн являются основателями теории игр) составляет понятие доминирования.

Определение 5.3. Дележ V₁(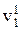, , 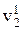…, 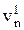) доминирует дележ
V₂(, , 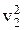…, 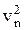) по коалиции К (обозначается V₁(К) > V₂(К)), если

и , i Î К.

Если V₁(K) > V₂(K), то справедливы утверждения.

1. Каждый член коалиции предпочитает дележ V₁ по сравнению с дележом V₂.

2. Так как , то члены коалиции К могут получить запланированный выигрыш при дележе V₁.

Принцип оптимальности Неймана-Моргенштерна утверждает, что лучшим решением игры n лиц является множество недоминируемых дележей.

Определение 5.4. Ядром игры n лиц называется множество недоминируемых дележей.

Таким образом, решение игры n лиц сведено к поиску ядра игры n лиц. Конструктивный поиск ядра позволяет провести следующая теорема.

Теорема 5.1. Дележ V = (v₁, v₂, …, v_n) принадлежит ядру n лиц тогда и только тогда, когда для любого подмножества К множества N выполняется условие

,

т.е. дележ V принадлежит ядру в том и только в том случае, когда для любой коалиции сумма выигрышей, входящих в коалицию игроков, не меньше, чем Ф(К).

Теорема 5.1 позволяет свести поиск ядра игры n лиц к решению системы неравенств.

П р и м е р 5.1 (продолжение). Найти ядро данной игры.

Решение. Для данной игры вектор V(v_A, v_B, v_C) является дележом, если

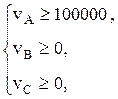(условия индивидуальной рациональности) (*)

v_A + v_B + v_C = 300000 (условие групповой рациональности).

Согласно теореме 5.1, дележ V принадлежит ядру в том и только в том случае, если выполнены неравенства:

v_A + v_B ³ 200000,

v_A + v_С ³ 300000,

v_В + v_С ³ 0, (**)

v_A + v_B + v_С ³ 300000.

Из системы (*) и (**) получим

v_B = 0, v_A + v_С = 300000, v_A ³ 200000.

Таким образом, любой вектор v (200000£ v_A£ 300000, v_B= 0, v_C = 300000 – v_A) принадлежит ядру игры.

Полученному решению можно дать следующую интерпретацию. Игрок С перебивает предложения игрока В и перекупает земельный участок по цене v_A (200000 £ v_A £ 300000), при этом выигрыш игрока С составит v_С = 300000– – v_A £ 100000, игрок В в данной игре не получает ничего. Очевидно, что полученное ядро содержит бесконечно много дележей. 5

 

П.4. Вектор Шепли

В некоторых играх участники не полагаются только на экономическую целесообразность. Стабильность коалиции, в которую в принципе могут «загнать» и принудительно, поддерживается с помощью третейского судьи (арбитра). Решения арбитра должны быть законом для всех участников игры. Такая разновидность кооперативных игр называется арбитражными играми.

Арбитражная схема игры используется в случае, когда дележ не устраивает игроков, но переходить к угрозам не хочется. Недовольные члены коалиции согласны воспользоваться решением арбитражного судьи.

Однако, для арбитра, если он действительно хочет стать арбитром, важно обеспечить не просто волевое, но справедливое решение. Конечно, и арбитр может допустить ошибку. Чтобы свести вероятность ошибки к минимуму, следует предельно формализовать процесс принятия решения. Это обеспечит беспристрастное отношение арбитра к игрокам.

Вектор Шепли является вариантом арбитражного дележа, который позволяет принять беспристрастное и справедливое решение. Вектор Шепли вводится аксиоматически. При данном способе дележа используется понятие «болвана», «носителя» и перестановки.

В данном случае понятие «болван» вовсе не означает, что у одного из игроков оригинальные умственные способности. Термин «болван» взят из популярной салонной игры.

В кооперативной игре болваном (b) называется тот игрок, присутствие которого в любой возможной коалиции не приносит коалиции никакой выгоды, кроме выигрыша болвана, т.е.

v(K È b) = v(K) + v(b).

Если игрок не является болваном, то он является носителем. Для носителя существуют коалиции, в которых он может принести пользу не только себе, но и своим товарищам. Носителем будем считать также множество всех болванов в игре n-лиц.

Основной задачей пункта будет указать способ, который ставит каждой кооперативной игре (т.е. каждой характеристической функции Ф(К)) некоторый вектор S(s₁, s₂, …, s_n), компоненты которого описывают справедливые в некотором смысле выигрыши каждого из игроков.

Справедливое решение при дележе выигрыша: носителя ничего не выделять на долю посторонних болванов, но и ничего не взимать с них. Математически это требование можно выразить следующим образом.

Аксиома эффективности. Если N – носитель некоторой кооперативной игры, то

.

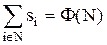Аксиома симметрии. Игроки, одинаково входящие в правила игры, должны по справедливости получить одинаковые выигрыши.

Аксиома линейности. Пусть на множестве одних и тех же игроков N имеются две игры Ф₁ и Ф₂. Если игрок i участвует в двух играх, то его выигрыши в этих играх должны складываться.

Можно показать, что приведенная система аксиом является непротиворечивой и полной в том смысле, что для всякой характеристической функции существует единственный вектор S(Ф), удовлетворяющий всем трем аксиомам. Этот вектор называется вектором Шепли.

Справедливы следующие утверждения.

Теорема 5.1. Каждая характеристическая функция имеет не более одного вектора Шепли.

Теорема 5.2. Для любой характеристической функции Ф(N) компоненты вектора Шепли S₁(Ф), S₂(Ф), …, S_n(Ф) вычисляется по формуле

.

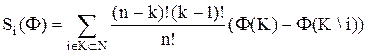Довольно часто в игре не так важен количественный результат игры, как сам факт победы. Примером тому являются выборы, в которых претенденту необходимо набрать абсолютное большинство голосов или преодолеть некоторый барьер. Так по закону РФ президентом страны становится претендент, набравший более 50% голосов (51% или 99%, в данном случае не играет главной роли). Претендент станет президентом, хотя полученные количественные результаты послужат для дальнейшего планирования действий руководства.

Если важен именно сам факт победы, то описание игры можно несколько упростить. Обозначим победу за 1, проигрыш – за 0. В этом случае, если игрок A_i не является болваном, то он обеспечивает своей коалиции победу, т.е.

Ф(К) – Ф(К \ i) = 1.

Если А_i «болван», то его выход из коалиции ей никак не повредит, поэтому

Ф(К) – Ф(К \ i) = 0.

Таким образом, формула для расчета вектора Шепли, приведенная в теореме 5.2, упрощается и имеет вид:

,

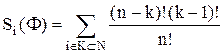где k – число участников определенной коалиции,

n – общее число участников.

Алгоритм применения вектора Шепли для кооперативной игры n лиц следующий:

1) рассматриваются все коалиции игрока i (i Î N);

2) вся прибыль игрока i по всем коалициям суммируется и усредняется по числу коалиций, в которых игроки N не «болваны».

Рассмотрим иллюстрирующий пример.

П р и м е р 5.2. Четыре акционера выбирают директора фирмы. Поскольку акционеры имеют разное число акций предприятия, то число голосов у них различно. Так 1-й выборщик (игрок А₁) владеет 5 голосами, 2-й выборщик (игрок А₂) – 20 голосами, 3-й выборщик (игрок А₃) – 35 голосами,
4-й выборщик (игрок А₄) – 40 голосами. Директор считается избранным, если за него проголосовала половина плюс еще один голос. Найти вектор Шепли S(s₁, s₂, s₃, s₄) этой игры.

Решение. Рассмотрим множество коалиций, которые могут избрать директора, т.е. выиграть.

{А₂; А₃} – 55 голосов;

{А₂; А₄} – 60 голосов;

{А₃; А₄} – 75 голосов;

{А₂; А₃; А₄} – 95 голосов;

{А₁; А₂; А₃} – 60 голосов;

{А₁; А₂; А₄} – 65 голосов;

{А₁; А₃; А₄} – 80 голосов;

{А₁; А₂; А₃; А₄} – 100 голосов.

Прочие коалиции, например {А₁; А₂} = 25 голосов, не могут набрать большинства при голосовании, поэтому выигрышными не являются.

Заметим, что игрок А₁ ни в одной коалиции не может принести победу. Поэтому во всех случаях он «болван». Значит,

S(A₁) = S₁ = 0.

Второй игрок в коалициях {А₂; А₃}, {А₂; А₄}, {А₁; А₂; А₃}, {А₁; А₂; А₄} может принести победу и не является «болваном». Рассмотрим, например, коалицию {А₁; А₂; А₃}, обладающую 60 голосами. Выход игрока А₂ из коалиции делает победу невозможной (60 – 20 = 40 < 51).

Для третьего игрока А₃ число коалиций, в которых он не является «болваном», также четыре: {А₂; А₃}, {А₃; А₄}, {А₁; А₂; А₃}, {А₁; А₃; А₄}.

Для игрока А₄ тоже существует четыре коалиции, в которых он не «болван»: {А₂; А₄}, {А₃; А₄}, {А₁; А₂; А₄}, {А₁; А₃; А₄}.

Всего случаев, когда игроки не «болваны» 0 + 4 + 4 + 4 = 12. Получаем:

,

,

,

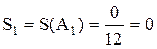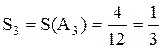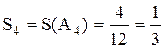
или S(0; 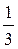, , 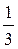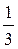).5

На первый взгляд, полученный результат кажется парадоксальным. Особенно парадоксальным, видимо, он кажется игроку А₄, который имеет число голосов вдвое больше, чем у игрока А₂.

Однако если немного вспомнить историю, то можно убедиться, что нередко партии, имеющие не так много голосов избирателей, маневрируя между более крупными партиями, добиваются больших успехов. Особенно богата такими примерами история древнего Китая, где враждовавших сторон, как правило, было больше двух. При этом две стороны находились в открытой конфронтации, как царства Вэй и У. Более слабый участник конфликта, царство Шу, поддерживало в конфликтах то одну, то другую сторону, что позволяло ему десятилетиями играть на равных с этими экономическими и военными монстрами.

Из не столь далекого прошлого памятны выборы премьер-министра Украины в 2006 году. В конфликте оранжевых и синих решающая часть голосов принадлежала партии социалистов. Ее присоединение к любой из двух сторон обеспечивало коалиции победу. Этим социалисты и воспользовались, получив в парламенте достаточное количество руководящих постов, в том числе и пост спикера парламента. При этом по числу голосов социалисты проигрывали основным партиям парламента. Если читателю интересно, он может самостоятельно рассчитать вектор Шепли для той политической игры и убедиться, что она закончилась совершенно справедливо с точки зрения арбитражной игры.

 

П.5. Игры с угрозами

Что может обеспечить устойчивость коалиции, если экономическая целесообразность не может удержать игроков от нарушения правил, а арбитр не обладает должной властью? Ответ – угроза. Угрозы, в отличие от арбитра, стабилизируют коалицию не извне, а изнутри. Традиционно считается, что прибегать к угрозам игроки должны в последнюю очередь, после того как все другие способы договориться исчерпаны.

Определение 5.3. Угрозой называют стратегию игрока, против которой у противников нет стратегии защиты. Игрока, обладающего стратегией угроз, называют лидером.

В кооперативной игре лидер может контролировать действия других игроков. Действительно, остальные игроки должны либо подчиниться требованиям лидера, либо подвергнуться наказанию.

Для использования стратегии угроз необходимо выполнение нескольких принципов.

1. Стратегия угроз должна заранее доводиться до сведения будущих участников коалиции и осуществляться, если соглашения нарушены.

2. Угроза должна быть действительно эффективна.

3. Наилучшей угрозой является та, которая не будет применена, но цель будет достигнута.

Для того чтобы игрок был лидером необходимо, чтобы:

1) дестабилизирующая стратегия угрозы была только у него;

2) лидер может обладать наименьшей полезностью среди других игроков, однако не может быть «болваном», иначе коалиция обойдется без него.

Справедливо следующее утверждение.

Теорема (существования) 5.3. В играх с постоянной суммой всегда существует хотя бы одна равновесная ситуация в стратегиях угроз.

В случае биматричных игр для поиска равновесной ситуации поступают следующим образом.

Пусть платежные матрицы игроков А и В имеют вид:

,

.

Составляется матрица Н = А – В. Далее рассматривается матричная антагонистическая игра. Если один из игроков имеет доминирующую стратегию, то он является лидером и может осуществлять угрозу. Если другой игрок не имеет доминирующей стратегии, то он беззащитен против угрозы. Если доминирующая стратегия есть, то игрок обладает контругрозой и с ним следует считаться.

Рассмотрим несколько примеров.

П р и м е р 5.3. Найти равновесную ситуацию в биматричной игре с угрозами, если

, .

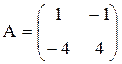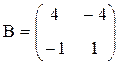Решение.

.

В данном случае игрок В имеет доминирующую стратегию В₁. Стратегии игрока А являются дублирующими, поэтому защиты от угрозы он не имеет. Значит, игрок В является лидером в данной игре. Оценим, насколько серьезна его угроза. Для этого определим равновесные ситуации в биматричной игре методом, предложенным в разделе 4. Геометрически полученное решение представлено на рисунке 5.1.

q 1 1/2   O 1/5 1 p

Рис. 5.1.

Получим,

.

Данное решение является устойчивым решением в смешанных стратегиях.

Предположим, что игрок В осуществил свою угрозу и выбрал стратегию В₁. Игрок А может либо подыграть ему, тогда v_А(А₁,В₁)= 1, v_А(А₁,В₁) =4, либо вредить, но в этом случае игрок А сам потеряет в четыре раза больше v_А(А₂, В₁)= – 4, v_В(А₂, В₂)= – 1.Таким образом, игрок А никак не может защититься от угрозы игрока В и ему с точки зрения экономической целесообразности следует согласиться на дележ v(A) = 1, v(B) = 4. 5

 

П р и м е р 5.4. Найти равновесную ситуацию в биматричной игре с угрозами, где

, .

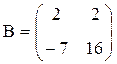Решение. В данной игре игрок А имеет доминирующую стратегию А₁ и гарантированный выигрыш v_*(А) = – 2. Игрок В также имеет доминирующую стратегию В₂ и гарантированный выигрыш v^*(В) = 2.

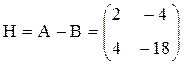.5

Судя по матрице Н, игрок В может претендовать на лидерство в игре, имея доминирующую стратегию В₂. Однако игрок А имеет против угрозы игрока В свою контругрозу – стратегию А₁, которая возвращает игроков к их максимальным гарантированным выигрышам, что делает кооперативную игру несущественной.

В этом случае игрок В не может диктовать свою волю игроку А, и дележ не должен осуществиться с помощью угроз.

⇐ Предыдущая12345678Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: