Примеры для самостоятельного решения

1. Некоторым НИИ разработана новая технология. Сам НИИ не может внедрить в производство новую технологию, но он может продать патент одной из двух фирм. При этом фирма, которой будет продана технология, получит 10000000 у.е.

а) Постройте характеристическую функцию игры.

б) Найдите ядро игры.

в) Найдите вектор Шепли указанной игры.

2. Проанализируйте биматричную игру примера 4.2, используя стратегию угроз.

 

Игры в нечетко определенной обстановке

П.1. Нечеткая игровая модель без проведения изучающего

Эксперимента

Рассмотрим следующую модификацию нечеткой игровой матричной модели (основные сведения о нечеткой логике приведены в Приложении А), предполагая, что игра носит уникальный (единичный) характер, не является антагонистической, содержит элементы неопределенности, которые трудно или невозможно отразить категориями теории вероятностей, но несложно выразить в лингвистической форме, решение игры допускается только в "чистых" стратегиях, предполагая дополнительно, что какой-либо изучающий эксперимент не проводится.

Многокритериальная модель с разнотипными критериями. Примем следующую математическую формулировку данной модели.

Дано:

1) множество вариантов {B_j}, , предполагаемых действий игрока 2 ("противника");

2) множество вариантов или стратегий {A_i}, , игрока 1 (ЛПР);

3) набор значений g_j () степеней уверенности о выборе игроком 2 той или иной стратегии;

4) набор критериев {J_q}, , определенных в количественной и/или в качественной форме.

Отметим, что анализ альтернатив по многим критериям – это важная задача принятия решений, которая возникает не только в военном деле, но и в технике, экономике, медицине и т. д.

Известные методики многокритериального анализа, которые используются, например, в технических системах, предусматривают преобразование вектора частных критериев, которыми оценивается система, к скалярному интегральному критерию. Существенное ограничение такого подхода состоит в том, что он плохо приспособлен к качественным критериям, которые оцениваются экспертными методами.

Методика, которая приводится ниже, не требует ни количественной оценки частных критериев, ни процедуры скаляризации. Она использует информацию о качестве вариантов в виде парных сравнений типа:

по критерию J^s вариант А₁ приблизительно такой же, что и вариант А₂ ;

по критерию J^t вариант А₁ немного лучше, чем вариант А₂ и т. п.

Задача состоит в том, чтобы упорядочить элементы множества {А_i} по критериям из множества Ω_J.

Для решения этой задачи предполагается использование следующих принципов:

Принцип 1: рассмотрение критериев как нечетких множеств, которые заданы на универсальных множествах вариантов с помощью функций принадлежности.

Принцип 2: определение функций принадлежности нечетких множеств на основе экспертной информации о парных сравнениях вариантов с помощью 9-бальной шкалы Саати [6а] (использование более 9 уровней нецелесообразно, поскольку из психологии известно, что в памяти человека удерживается одновременно не более 7±2 понятий [20]).

Принцип 3: ранжирование вариантов на основе пересечения нечетких множеств – критериев, которые отвечают известной в теории принятия решений схеме Беллмана-Заде [2].

Принцип 4: ранжирование критериев методом парных сравнений и учет полученных рангов как степеней концентрации соответствующих функций принадлежности.

 

Критерии как нечеткие множества.

Пусть 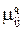- число в диапазоне [0,1], которое характеризует уровень оценки варианта по критерию J^q Î Ω_J при условии, что противником выбран вариант B_j (чем больше число 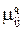, тем выше оценка альтернативы по критерию 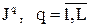). Тогда критерий = J^q(B_j) при выборе варианта B_j можно представить в виде нечеткого множества, заданного следующим образом:

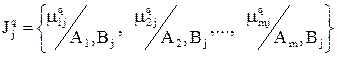. (6.1)

 

Чтобы определить степени принадлежности, входящие в (6.1), воспользуемся следующим методом.

Сформируем матрицы парных сравнений альтернатив по каждому критерию при условии, что противником принята стратегия B_j..

Для критерия матрица парных сравнений имеет вид:

 

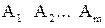
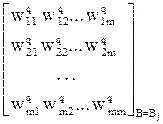, (6.2)

 

где элемент 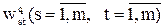оценивается экспертом по 9-бальной шкале Саати:

1 – если отсутствует преимущество альтернативы A_t над альтернативой A_s;

3 – если имеется слабое преимущество A_t над A_s;

5 – если имеется существенное преимущество A_t над A_s;

7 – если имеется явное преимущество A_t над A_s;

9 – если имеется абсолютное преимущество A_t над A_s;

2, 4, 6, 8 – промежуточные сравнительные оценки.

Знание матрицы (6.2) позволяет с использованием метода Саати проранжировать каждую альтернативу по каждому критерию J^q Î Ω_J при условии варианта противника . Для вычисления рангов в соответствии с методикой, предложенной в работах [49, 50], необходимо найти собственный вектор матрицы (6.2). Для получения первых приближений искомых характеристик рангов можно воспользоваться следующей процедурой, предполагающей, что матрица (6.2) имеет следующие свойства:

- элементы ее главной диагонали равны единице, т. е.

;

- элементы, симметричные относительно главной диагонали, связаны зависимостью

;

 

- матрица является транзитивной, т. е.

 

.

 

Наличие таких свойств позволяет определить все элементы матрицы (6.2) по элементам одной из строк. Если известна g-я строка, т. е. элементы , то произвольный элемент определяется так:

.

После определения всех элементов матрицы (6.2) степени принадлежности, необходимые для формирования нечеткого множества (6.1), как можно показать, вычисляются по формуле:

 

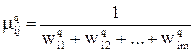, i = , (6.3)

 

(напоминаем, что элементы здесь соответствуют условию B = B_j).

Равновесные критерии. Базируясь на приведенном принципе Беллмана-Заде, наилучшей системой будем считать ту, которая одновременно лучше по критериям J¹, J²,…, J^L. Поэтому нечеткое множество, которое необходимо для рейтингового анализа, определяется – для i,j-го сценария игры – в виде пересечения (интегральный критерий оценки систем)

 

.

 

Учитывая, что в теории нечетких множеств операции пересечения соответствует min, а также степени доверия к выбору противником j-го варианта игры B_j, получаем:

 

. (6.4)

 

В соответствии с логикой приведенных рассуждений, наилучшей будет альтернатива A_g, для которой величина μ_g является наибольшей, т. е.

 

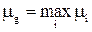. (6.5)

 

Заметим, что после определения значений 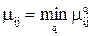с рассматриваемой моделью игры можно сопоставить некоторую модифицированную матрицу вида табл. 6.1.

 

Таблица 6.1

Модифицированная матрица выигрышей 1-го игрока

Bj Ai	B1	B2	...	Bj	...	Bn
A1	μ11	μ12	...	μ1j	...	μ1n
A2	μ21	μ22	...	μ2j	...	μ2n
. . .	. . .	. . .	...	. . .	...	. . .
Ai	μi1	μi2	...	μij	...	μin
. . .	. . .	. . .	...	. . .	...	. . .
Am	μm1	μm2	...	μmj	...	μmn

 

Особенностью этой модели является, во-первых, то, что элементы матрицы принадлежат единичному отрезку (μ_ij Î [0, 1]) и, во-вторых, то, что имеется информация о значениях g_j () степеней уверенности о выборе игроком 2 той или иной стратегии.

Неравновесные критерии. Пусть v₁, v₂,…, v_L – коэффициенты относительной важности (или ранги) критериев J¹, J²,…, J^L такие, что v₁+v₂+…+v_L=1. Для определения коэффициентов v₁ ¸ v_L необходимо сформировать матрицу парных сравнений важности критериев J^q Î Ω_J, аналогичную (6.2), и воспользоваться формулой (6.3).

При наличии коэффициентов важности , соотношение (6.4) принимает вид

, (6.6)

 

где степени v_q свидетельствуют о концентрации нечеткого множества в соответствии с мерой важности критерия v_q..

Окончательный выбор альтернативы осуществляется, как и выше, с помощью соотношения (6.5).

Отметим, что рассмотренный подход, вообще говоря, не позволяет прямо определить выигрыш первого игрока в количественной форме, что и не удивительно, поскольку в число исходных входила предпосылка о разнотипности критериев, т.е. в их число входили как качественные, так и количественные показатели. Такую оценку можно найти, если все критерии имеют чисто количественный характер.

Многокритериальная модель с количественными критериями. Выбор альтернативы в многокритериальной задаче на основе нечеткой матричной модели при наборе чисто количественных критериев производится следующим образом.

Пусть, как и ранее, оба игрока придерживаются только чистых стратегий A₁¸A_m и B₁¸B_n, при этом первый игрок ничего не знает о стратегии, которую выберет второй игрок, игра носит уникальный (единичный) характер и отображается матрицей выигрышей 1-го игрока, элементы которой являются векторами

 

, , , (6.7)

 

с элементами (), отражающими выигрыши 1-го игрока ( в случае выбора им стратегии A_i, а вторым игроком – стратегии B_j) по одному из L частных количественных критериев J^q, т.е.

 

= J^q(i,j). (6.8)

 

В условиях приведенной игровой модели требуется определить такую чистую стратегию A_q 1-го игрока, при которой обеспечиваются его наибольший обобщенный в каком-то смысле выигрыш по всем частным критериям.

Алгоритм решения. Решение поставленной задачи обеспечивается следующей последовательностью действий.

1. Определяются (например, экспертным путем) минимальные и максимальные возможные значения критериев и производится их приведение к единичному масштабу:

(6.9)

(при этом Î[0, 1]).

2. Каждый критерий рассматривается как лингвистическая переменная, значениями которой являются не более 9 термов, например, уровни "пренебрежимо малый", "очень малый", "малый", "средний", "небольшой", "большой", "очень большой" и т.п. Далее на единичном отрезке [0, 1], рассматриваемым как универсальное множество [1], задаются функции принадлежности данных уровней какого-либо типового вида, например, в виде функций Гаусса, треугольных или колоколообразных [1,11], в частности, так, чтобы они равномерно покрывали указанный отрезокм. нь большой".оличественных критериев производится оличественный характер. первого игрока в количественной форме, что и не.

3. Для каждой возможной пары стратегий A_i, B_j выигрыши по каждому критерию задаются и рассматриваются как некоторый терм с соответствующей функцией принадлежности 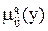из числа заданных (y Î[0, 1]), например: при стратегиях A₁ и B₂ по первому критерию выигрыш – "очень малый", по второму – "средний" и т.д. Значения термов для пар стратегий устанавливаются путем опроса экспертов [14].

4. В соответствии с принципом Беллмана-Заде, наилучшей стратегией 1-го игрока будет считать та, которая одновременно лучше по критериям a¹, a²,…, a^L. Поэтому нечеткое множество, которое необходимо для рейтингового анализа, как и выше, определяется – для i,j-го сценария игры – в виде пересечения (интегральный критерий оценки систем)

 

. (6.10)

 

Используя для реализации операции пересечения операцию взятия минимума min, для функции принадлежности такого обобщенного критерия получаем:

. (6.11)

 

Четкое значение выигрыша a_ij* для i,j-го варианта определяется в результате выполнения дефаззификации [1,11], например, как значение аргумента функции , соответствующее ее наибольшему значению:

a_ij* = . (6.12)

Если такой максимум достигается одновременно на некотором множестве точек, то в качестве a_ij* можно брать, например, их среднее значение.

5. После вычисления a_ij* (, ) матричная игра становится похожей на обычную (классическую) матричную игру двух игроков с матрицей выигрышей (четкой) вида табл. 6.2.

 

Таблица 6.2

Модифицированная матрица выигрышей 1-го игрока

Bj Ai	B1	B2	...	Bj	...	Bn
A1	a11*	a12*	...	a1j*	...	a1n*
A2	a21*	a22*	...	a2j*	...	a2n*
. . .	. . .	. . .	...	. . .	...	. . .
Ai	ai1*	ai2*	...	aij*	...	ain*
. . .	. . .	. . .	...	. . .	...	. . .
Am	am1*	am2*	...	amj*	...	amn*

 

Единственным отличием от классического варианта в данном случае является наличие, как и выше, набора значений g_j () степеней уверенности о выборе игроком 2 определенной стратегии.

В соответствии с методами нечеткой логики и приведенными рассуждениями, наилучшей будет альтернатива A_g, для которой величина усредненного выигрыша будет наибольшей. В соответствии с алгоритмом Сугэно, такой средний выигрыш для i-й стратегии 1-го игрока определяется соотношением:

. (6.13)

 

Очевидно, первый игрок должен выбирать стратегию A_g, обеспечивающую наибольший выигрыш:

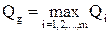. (6.14)

Последняя формула и является, по сути, решением поставленной задачи, определяя при этом и средний выигрыш.

Отметим, что изложенное относилось к случаю равноправных (равновесных) критериев. При неравновесных критериев рассмотренный алгоритм вполне применим, аналогично ранее рассмотренному подходу.

Пусть v₁, v₂,…, v_L – коэффициенты относительной важности критериев J¹, J²,…, J^L (такие, что v₁+v₂+…+v_L=1). В этом случае формула (6.11) модифицируется к виду

 

, (6.15)

 

и рассмотренный выше алгоритм может быть использован без каких-либо других его изменений.

П р и м е р 6.1. Пусть выигрыши первого игрокапо двум равновесным критериям, выраженные в качественной (лингвистической) форме, отражаются табл. 6.3.

 

Таблица 6.3

Исходная матрица выигрышей к примеру 6.1

Bj Ai	B1	B2
A1	(м,б)	(с,с)
A2	(б,с)	(м,с)
A3	(б,м)	(б,б)

 

Здесь "м" означает малый выигрыш, "с" – средний, "б" – большой. Соответствующие функции принадлежности треугольного вида приведены на рис. 6.1.

 

 

1

m_м(y) m_с(y) m_б(y)

 

y

 

0 0.5 1

 

Рис. 6.1. Функции принадлежности к примеру 6.1

 

Пусть, далее, заданы: γ₁ = 0.4, γ₂ = 0.8.

Требуется определить оптимальную стратегию первого игрока.

Решение. В соответствии с формулами (6.11), (6.12), от приведенной матрицы выигрышей можно придти к модифицированной матрице выигрышей вида табл. 6.4.

Таблица 6.4

Модифицированная матрица выигрышей

 

Bj Ai	B1	B2
A1	0.5	0.5
A2	0.75	0.25
A3	0.5

 

 

По данной матрице и при использовании соотношений (6.13), ((6.14) получаем 5/6, т.е. g = 3, и в данном случае наилучшей является стратегия (альтернатива) A₃.

Ранжирование равнозначных альтернатив. Иногда возможны ситуации, когда в результате процесса нахождения решения, одновременно несколько альтернатив (стратегий) являются наилучшими, т.е. им, например, соответствуют одинаковые средние выигрыши и т.п. Такие альтернативы будем называть равнозначными. Возникает вопрос: если все-таки необходимо выбрать одну-единственную альтернативу, то какая из равнозначных является предпочтительней?

Можно предложить, по крайней мере, три возможных подхода для ответа на данный вопрос.

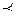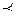Первый: экспертным путем провести ранжирование среди равнозначных альтернатив, чтобы можно было установить последовательность предпочтений, например, A₃ A₄ A₂ 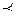A₇, где A₂, A₃, A₄, A₇ – отобранные равнозначные альтернативы. Этот подход, однако, как представляется, вносит дополнительный субъективизм в процесс принятия решения и вряд ли, поэтому, является наилучшим.

Второй подход основан на исследовании чувствительности альтернатив к неточности исходной (экспертной) информации. Его обоснованием является принцип: среди равнозначных альтернатив наиболее предпочтительной является альтернатива, наименее чувствительная к изменениям заданной исходной (априорной) информации.

Этот подход рассмотрим вначале для частного случая – когда все критерии имеют количественный вид, а неточность исходной информации может проявляться только в неточности задания значений γ_j.

Обратимся к формуле (6.13), положив в ней, для простоты, что значения γ_j пронормированы, так что (заметим, что перейти к нормированным значениям γ_j достаточно легко). При этом будем иметь

= γ ^T× a_i*, (6.16)

где γ ^T = (γ₁, γ₂,…, γ_n) – транспонированный вектор степеней принадлежности γ_j, a_i* = (a_i1*_, a_i2*,…, a_in*)^T – вектор с элементами i-й строки преобразованной (см. табл. 6.2) матрицы выигрышей.

Используя аппарат матричного анализа, для модуля вектора-градиента из (6.16) получаем:

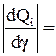| a_i* |. (6.17)

На основании приведенного принципа и последнего выражения, среди равнозначных альтернатив наилучшей будет та, для которой модуль соответствующей ей вектора-строки преобразованной матрицы выигрышей будет наименьшим.

П р и м е р 6.2. Пусть модифицированная матрица выигрышей имеет вид табл. 6.5, при этом γ₁ = 0.4, γ₂ = 0.6 (γ₁ + γ₂ = 1).

Таблица 6.5

Модифицированная матрица выигрышей

 

Bj Ai	B1	B2
A1	0.5	1.0
A2	1.25	0.5
A3	0.6	0.8

 

В соответствии с формулами (6.13), (6.14), получим, что две альтернативы – A₁ и A₂ в данном случае являются равнозначными, приводя к средним значениям выигрыша Q₁ = Q₂ = 0.8.

В то же время, при использовании евклидовой нормы вектора, здесь = 1.118, 1.346. Следовательно, целесообразен выбор первой альтернативы, как менее чувствительного решения.

Анализ чувствительности по отношению как к параметрам γ_j, так и к элементам a_ij* матрицы вида табл. 6.2, дает следующее выражение для вектора частных производных (вектора-градиента)

 

. (6.18)

 

Модуль этого вектора (в евклидовой метрике)

 

. (6.19)

 

Нетрудно видеть, что большие значения данного модуля будут у решений (альтернатив) с большими значениями γ_j, a_i*,т.е.наилучшие, в смысле соотношения (6.14), решения в данном случае являются и наиболее чувствительными к неточности задания начальных условий игры.

Нахождение вектора коэффициентов чувствительности для случая разнотипных критериев, т.е. для модели, которой соответствует матрица вида табл. 6.1, проведем, используя вспомогательную формулу для частной производной выражения

a = min (β₁, β₂,…, β_n). (6.20)

 

Для нахождения этой вспомогательной формулы, представим (6.20) следующим образом:

, (6.21)

 

где 1[×] – единичная ступенчатая функция Хевисайда [19].

Функция, определяемая (6.21), является непрерывной и дифференцируемой, при этом, как нетрудно видеть,

 

= (6.22)

 

Используя приведенный результат, отметим, что у вектора-градиента = все элементы, кроме одного, будут нулевыми, и лишь один элемент будет равен единице. Отмеченное обстоятельство позволяет записать:

= 1. (6.23)

 

Сопоставление теперь выражений (6.20) и (6.4) и принятие во внимание формулы (6.23) позволяет сделать вывод, что в модели нечеткой матричной игры, рассмотренной выше, все альтернативы имеют одинаковую чувствительность по отношению к начальным условиям игры, при этом данная чувствительность от этих условий не зависит.

Изложенное, как представляется, позволяет сформировать достаточно интересный промежуточный вывод о свойствах нечетких матричных игр, но, одновременно показывает, что рассматриваемый (второй) подход для выделения наилучшей альтернативы из ряда равнозначных в данной ситуации неприменим.

Очевидно, для случая разнотипных критериев, по-видимому, более пригоден третий подход. Здесь для выбора наилучшей из ряда равнозначных альтернатив, сначала, на основании найденных по (6.3) значений 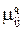, составляется преобразованная матрица игры A вида табл. 6.1, т.е. с элементами

, ,

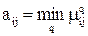(заметим, что, очевидно, 0£ a_ij ≤ 1).

Затем составляется так называемая матрица шансов i-й альтернативы , которая определяется следующим образом:

– элементы i-й строки матрицы равны элементам i-й строки матрицы A,

– элементы всех остальных строк определяются как разность ; их можно интерпретировать как шансы, упущенные остальными альтернативами.

Наконец, вычисляется обобщенная степень соответствия альтернатив заданным критериям, определяемая как

 

. (6.24)

 

Предпочтение отдается альтернативе с наибольшим значением G_i.

П р и м е р 6.3. Пусть преобразованная матрица A отображается табл. 2.4 с элементами μ_ij, и γ₁ = 0.4, γ₂ = 0.8. Нетрудно видеть, что применение подхода, изложенного ранее, приводит при этом к двум равнозначным альтернативам – A₁ и A₃ со значениями μ₁ = μ₃ = 0.4.

Применение же подхода с использованием матриц шансов дает:

 

, ,

 

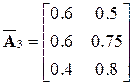
и (с использованием формулы (6.24))

G₁ = 0.3, G₂ = 0.23, G₃ = 0.38.

В итоге равнозначность исчезает, наилучшей следует признать третью альтернативу (стратегию) A₃.

Строгого обоснования этот третий подход не имеет и может быть пояснен только интуитивно. Тем не менее, проверка на модельных примерах показывает его применимость для рассматриваемой задачи.

 

⇐ Предыдущая12345678Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: