 |
Модели бетона, железобетона, фундаментов зданий и сооружений
|
|
|
|
В последние годы появились выдающиеся монографии [1, 12] по моделям силового сопротивления железобетона. Они отличаются глу-биной и обоснованностью положений, учётом большого числа влияю-щих факторов: трещин и схем армирования (Н.И. Карпенко), реологи-ческих свойств (В.М. Бондаренко, В.И. Колчунов). Работы [1, 12] яв-ляются надёжной базой для совершенствования теории расчёта и про-ектирования конструкций.
2.1. ДЕФОРМАЦИОННАЯ МОДЕЛЬ
Анализ модели сделали А.С. Залесов и Т.А. Мухамедков [11]. К железобетонным конструкциям представляются требования прочно-сти, устойчивости, эксплуатационной пригодности, долговечности и надёжности. Особенностями железобетона как композитного материа-ла являются: образование и развитие трещин в бетоне, нелинейные свойства бетона и арматуры, реологические свойства бетона, изме-няющиеся во времени. Указанные особенности могут быть реализова-ны через физические свойства, связывающие напряжения и деформа-ции бетона и арматуры. Они определяются на основе обобщённого закона Гука для анизотропного тела.
Деформационные модели разработаны для линейных и плоских элементов при одноосном и двухосном напряжённо-деформированном состояниях при действии изгибающих, крутящих моментов и продоль-ных сил.
Согласно евростандартам, деформационная модель основывается на четырёх гипотезах:
а) плоских сечений;
б) считают известными зависимости напряжения–деформации для бетона и арматуры;
в) диаграммы напряжения–деформации при неоднородном на-пряжённом (вследствие изгиба) состоянии получают из опытов по од-нородному напряжённому состоянию простого сжатия или растяжения;
г) считают совпадающими нейтральные оси напряжений и де-формаций при длительном загружении.
|
|
|
Первая гипотеза является условием совместности деформаций бе-тона и стали железобетонного элемента. Основное условие примени-мости этой модели – малость сдвигов по сравнению с углами поворота.
Вторая гипотеза позволяет по известным относительным дефор-мациям рассчитать напряжения бетона и арматуры в различных точках сечения. Для бетона используется криволинейная диаграмма с ниспа-дающей ветвью.
Из анализа деформационной модели следует частный предельный случай пластического шарнира. Зоны пластического растяжения– сжатия снижаются. Эпюра напряжений в сжатой зоне бетона достигает прямоугольного очертания. Кривизна изогнутой оси элемента в этом сечении равна бесконечности.
Для линейных железобетонных элементов. Модель включает уравнения равновесия внешних и внутренних сил, условия деформи-рования в виде гипотезы плоских сечений и полные диаграммы, свя-зывающие напряжения и деформации в бетоне и арматуре.
В результате решения получают систему уравнений, связываю-щих изгибающие моменты в двух направлениях, продольные силы с кривизнами в двух направлениях и продольными деформациями через жёсткостные характеристики.
Для плоских элементов рассматривается выделенный элемент с изгибающими и крутящими моментами, сдвигающими и нормальными силами, действующими по боковым сторонам.
Деформационная модель определяется из уравнений равновесия внешних усилий, действующих по боковым сторонам, внутренних уси-лий в диагональном нормальном сечении в виде гипотезы плоских сече-ний и полных диаграмм напряжения–деформации в бетоне и арматуре.
Как и для линейных элементов, в плоских получают систему уравнений, связывающих изгибающие и крутящие моменты, продоль-ные и сдвигающие силы в двух взаимно перпендикулярных направле-ниях с кривизнами, усилиями закручивания и сдвиге, продольными деформации через жёскостные характеристики элементов.
|
|
|
В деформационной модели используются диаграммы криволи-нейные, упрощённые трёхлинейные, включающие условно упругий, неупругий и условно пластический участки, двухлинейные по типу диаграммы Прандтля.
В качестве условия деформирования сечения принята гипотеза плоских сечений. Критериями прочности допускается принимать де-формации бетона и арматуры некоторых предельных значений.
В деформационной модели допускается сжатая зона над трещи-ной и растянутая с трещиной. Учитывается работа растянутого бетона между трещинами. Имеется возможность выполнять расчёты с учётом физической и геометрической нелинейности по прочности, устойчиво-сти, деформативности и трещиностойкости; расчёт систем и элементов различной конструкции и состава.
В новых нормативных документах допускаются упрощённые рас-чёты на прочность (основанные на методе предельного равновесия), деформации (основанные на учёте первых условно линейных участков двухлинейных диаграмм бетона и арматуры), трещиностойкости (в условии упругой постановки с понижающим модулем упругости сжа-того бетона и повышающим за счёт влияния растянутого бетона между трещинами).
Рекомендуется разработка таких расчётных моделей и методов расчёта, которые позволяли бы инженеру понимать и оценивать харак-тер работы конструкций в целом.
Предусматривается разработка общего метода расчёта долговеч-ности железобетонных конструкций с прямым учётом фактора време-ни; разработка методов расчёта железобетона, основанных на общих правилах строительной механики и единых расчётных моделях. Кон-кретные особенности элементов следует учитывать введением допол-нительных запасов.
Расчёт высотных зданий производится как пространственной сис-темы с учётом податливости основания, а несущей системы и отдель-ных элементов – с учётом физической и геометрической нелинейно-
сти. Рекомендуется стремиться к более простым конструктивным сис-темам регулярных в плане и по высоте, с совмещёнными центрами тяжести и жёсткости, с разрезкой деформационными швами распо-знающих блоков здания, уделять внимание повышению сопротивления внешних специальных воздействий, например, при выходе из строя одного конструктивного элемента или его части.
|
|
|
Расчёт прочности по нормальным сечениям железобетонных кон-струкций при действии изгибающих моментов и продольных сил про-водят на основе деформационной модели.
Модель для расчёта прочности включает:
– уравнения равновесия внешних и внутренних сил в нормальном сечении
|
|
i i
|
|
|
– уравнения, устанавливающие распределение деформаций в бе-тоне и арматуре по нормальному сечению исходя из условия плоского поворота и плоского смещения сечения (гипотезы плоских сечений):
|
|
|
|
– уравнения, определяющие связь между напряжениями и отно-сительными деформациями бетона и арматуры:
|
В уравнениях (*) – (***) Mx, My, N – изгибающие моменты в
|
|
центра тяжести j -го стержня арматуры, напряжение и деформация в нём; e0– относительная деформация волокна, расположенного на пе-
|
ствия моментов Mx, My.
За расчётные диаграммы состояния сжатого бетона принимают криволинейную диаграмму с ниспадающей ветвью или более простые диаграммы трёхлинейную и двухлинейную – ипа диаграммы Прандтля. Для высокопрочных арматурных сталей принимают криволиней-
ную, трёхлинейную или двухлинейную диаграммы.
Расчёт прочности по нормальным сечениям железобетонных кон-струкций производят путём решения приведённой выше системы уравнений. При этом прочность сечения проверяют из условий
|
|
|
e b max£ e b, ult;
e s max£ e s, ult,
|
Рис. 6. Расчётная схема нормального сечения железобетонного элемента
Предельные относительные деформации сжатого бетона при дву-значной эпюре деформаций в нормальном сечении принимают равны-
|
|
интерполяции.
|
Для общего случая система уравнений для расчёта прочности по деформационной модели имеет вид:
|
|
|
|
|
|
|
Коэффициентыупругости i -гоучасткабетонаn bi и j -гостержняарматуры n sj определяют по формулам:
|
|
|
диаграмм состояния бетона и арматуры.
Мурзенко А.Ю. предложен метод расчёта фундаментов по шести критериальным состояниям. Введено понятие о критериальных на-грузках, соответствующих определённому количественному состоя-нию конструкции и имеющих количественные нормативные ограниче-ния по СНиП.
Состояния 1 и 2 относятся к условиям работы по второй группе предельных состояний; 1 – соответствует стадии работы до образова-ния трещин; 2 – в условиях образования раскрытия трещин.
Состояния 3 и 4 относятся к расчётам по предельным состояниям первой группы и соответствуют условиям статического метода пре-дельного равновесия. Критериальная нагрузка для состояния 3 опреде-ляется из условия N £ N 3, где N 3– определяется из расчёта по несущей способности статическим методом предельного равновесия. Состояние 4 относится к расчёту фундамента на продавливание плитной части. При этом должно выполняться условие N £ N 4, где N 4определяется из ус-ловия расчёта на продавливание. Фактически при N = N 4ещё не про-исходит исчерпание несущей способности на продавливание, так как в расчёте не учитываются упрочнение бетона в сжатой зоне сечения, действительная форма призмы продавливания и реактивные эпюры давления с учётом перераспределения напряжений в основании, а так-же концентрация реактивных давлений в основании призмы продавли-вания. Вследствие этого общее сопротивление продавливанию повы-шается и в рассматриваемых состояниях система имеет значительные внутренние резервы несущей способности.
|
|
|
За счёт образования трещин в фундаменте формируются упруго-пластические шарниры, которые разделяют плитную часть на жёсткие звенья и превращают фундамент в кинематическую систему. Это позво-ляет перейти от расчёта в одном, наиболее нагруженном сечении, к рас-чёту плитной части в целом как статически неопределимой системы.
Состояние 5 соответствует исчерпанию несущей способности по кинематической схеме работы на изгиб, а 6 – на продавливание с учё-том перераспределения усилий в материале фундамента и грунте ос-нования, упрочнения бетона сжатой зоны.
Нижний предел несущей способности определяется из условия статического равновесия и предельных условий, верхний – из рассмот-рения кинематически возможных состояний конструкции. Эти преде-лы образуют зону, в пределах которой может быть назначена расчёт-ная нагрузка с учётом надёжности и риска.
Основной целью расчёта и проектирования является обеспечение нормальной эксплуатации объектов в течение заданного периода вре-мени, прогноз возможных изменений контролируемых параметров.
2.2. МОДЕЛИ ФУНДАМЕНТНЫХ ПЛИТ
Разработке методов расчёта фундаментных плит и балок посвя-щены труды: Винклера, Б.Г. Коренева, В.З. Власова, М.М. Филоненко-Бородича, П.Л. Пастернака, Б.Н. Жемочкина, А.П. Синицина, Н.Н. Ле-онтьева, М.И. Горбунова-Посадова, И.А. Симвулиди, А.А. Мустафае-ва, А.П. Пшеничкина, В.И. Травуша, А.Г. Юрьева и других. Анализ моделей грунтовых оснований и фундаментных конструкций дан в [2, 3, 5, 8, 9, 13, 16 – 20, 23 – 28].
|
|
|
|
Для модели основания с двумя упругими характеристиками
p (x, y = k 1 (x, y) k 2 (x, y
2 2
,гдеD = +;
¶ x ¶g
k 1и k 2– соответственно первая и вторая упругие характеристики; k 1имеет размерность кг/см², а k 2– кг/см.
|
w(x, y)= 1- v 0 ¥¥ E 0 -¥-¥
r x,h d x d h
|
В отдельных случаях реактивное давление на некоторой части плиты может быть отрицательным (растягивающим).
В процессе расчёта определяются перемещения, усилия и размеры зоны контакта. В пределах зоны контакта остаются справедливыми уравнения, учитывающие реакцию упругого основания, а в зоне отрыва балка или плита работает как свободная, т.е. на неё действуют только те активные нагрузки, которые приложены к этой части конструкции.
Юрьев А.Г. предложил методику оценки НДС полов промышлен-ных зданий. Механические характеристики основания зависят от гео-метрических и физических параметров конструкции. Физической мо-делью пола принята многослойная плита на упругом основании. Раз-работана математическая модель для многослойной плиты на двухпа-раметрическом основании с характеристиками, полученными на ва-риационной основе.
При
U = V = 0 W = (x, y, z) = w1(x, y) Ф(z),
где w1(x, y) – вертикальные перемещения верхней поверхности основа-ния; Ф(z) – функция вертикального распределения перемещений.
По методу Ритца–Тимошенко
w1(x, y) = BX (x) · Y (y),
где X (x), Y (y) – функции, отражающие прогиб плиты. Работа внешних сил
D = (U – T) = 0,
где U – потенциальная энергия деформирования основания плиты. Усовершенствованная двухпараметрическая модель В.З. Власова
обладает распределительным свойством по трём направлениям.
Для многослойной плиты нейтральный слой смещается на вели-чину е.
Цилиндрическая жёсткость определяется из уравнения:
|
|
1 V - t /2- e
где t – толщина многослойной плиты.
В процессе эксплуатации зданий происходит накопление разного рода повреждений за счёт усталости, коррозионного износа, неблаго-приятных внешних воздействий.
Критерии повреждённости бетона представляют в виде:
D = (t)/ u,
где e u – предельные деформации.
Уравнение повреждённости модели (определено из фундамен-тального реологического уравнения) имеет вид:
En &(t) + H e(t) n &(t) + (t)
и выражается в виде
EndD / dt + HD [ nV s+ E s(t)]/ e u,
где Н – длительный модуль упругости, соответствующий предельным деформациям; Е – мгновенный модуль упругости; n = h /E – время ре-лаксации; h – параметр вязкости.
|
|
Расчётные модели оснований для балок, плит и зданий подробно рассмотрены в [24]. Особое внимание уделено неоднородным в плане основаниям. Так, зависимость между реакцией основания и его осад-кой имеет вид
p x, y с (x, y)w (x, y.
Дифференциальное уравнение изгиба плиты с переменным коэф-фициентом с (x,y) представляют в виде:
D Ñ 4w (x, y)+ с (x, y)w x, y)= q x, y,
а изгиба балки
|
|
Рассмотрим предложения В.В. Болотина, Д.Н. Соболева, Б.П. Ма-карова.
Для статически неоднородного упругого полупространства
|
где p (x, y –математическоеожиданиереактивногодавлениянапо-лупространство; p x, y)–собственнослучайноереактивноедавление.
Здесь учтён метод эквивалентного слоя Н.А. Цытовича. Для пли-ты дифференциальное уравнение представлено в виде системы:
|
|
В [20] дан анализ расчётных моделей системы «сооружение– основание» как монолитных балок с проёмами, сопротивляющихся изгибным и сдвиговым деформациям (Б.Д. Васильев, Б.И. Далматов, Д.Д. Сергеев, и др.); в виде призматических оболочек (Б.А. Косицын, Б.С. Васильков, В.И. Лишак, А.П. Пшеничкин).
Дифференциальные уравнения изгиба и кручения оболочки име-ют вид:
|
|
|
|
|
|
|
контура поперечного сечения коробки.
Осадка здания рассматривается как аддитивная случайная функ-
|
Sik (x, y)= Sikx, y + Sikx, y,
|
2.3. ПРИЗМАТИЧЕСКИЕ И ПИРАМИДАЛЬНЫЕ СВАИ
Сопротивляемость просадочных грунтов оснований поперечным воздействиям, очевидно, так же как и фундаментов неглубокого зало-жения, будет изменяться в соответствии с закономерностями продви-жения влаги при случайном увлажнении оснований. Поэтому в рас-чётной схеме коэффициент жёсткости каждого прорезаемого конст-рукцией просадочного грунта становится переменным по глубине. Функция жёсткости EJ (x) в зависимости от особенности изгибаемой конструкции может быть непрерывной по всей глубине опоры или же кусочно-непрерывной в пределах каждого прорезаемого ею слоя грун-та. Характер функции k (x), отображающей взаимодействие грунта с конструкцией, будет зависеть от многих факторов (от свойства и сте-пени просадочности грунтов, особенности конструкции, её загружения и др.). Представить эту функцию в общем виде для всех встречающих-ся в практике случаев пока ещё не представляется возможным. В пер-вом приближении для назначения вида функции k (x) можно исходить из применяемых в расчётах свай на горизонтальную нагрузку законов нарастания сопротивляемости грунта по глубине. В литературе встре-чаются различные предложении по данному вопросу. Так, например, в рекомендациях по расчёту фундаментов глубокого заложения опор мостов грунт рассматривается как упругая линейно-деформируемая среда, характеризуемая коэффициентом постели
k (x) = mbx,
где m – коэффициент, зависящий от свойств грунта, т/м4; х – глубина расположения точки от поверхности грунта.
В работе И.В. Урбана коэффициент постели с учётом перехода грунта в состояние предельного равновесия на поверхности грунта принимается нарастающим с глубиной по линейному закону
|
где kh – коэффициент постели грунта в горизонтальном направлении на глубине h.
На основании экспериментальных данных Риффат рекомендуют принимать
|
|
где kh– предельное значение коэффициента на лубине h; b – экспе-
риментально определяемый параметр, учитывающий нелинейность изменения сопротивляемости грунта по глубине. По данным опыта Риффата, b = 0,02.
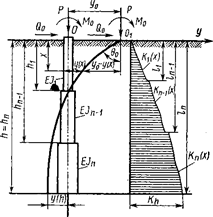Рис. 7. Расчё ная схема гибких фундаментов глубокого заложения при продольно-поперечном изгибе
Воспринимаемое конструкцией внешнее воздействие в общем случае ожет быть сведено на уровне поверхности грунта к комбина-ции вертикальной Р и поперечной нагрузок Q 0 а также момента М 0. Расчёт заглублённой в грунте опоры статически тождествен расчёту балки, свободно лежащей па сплошном упругом сновании перемен-ной опротивляемости, находящейся под действием приложенных на одном из концов поперечной нагрузки Q 0и момента М 0, а также про-дольной силы Р В случае гибкого фундамента с уширенной подошвой добавляются реакции упругого защемления подошвы в виде момента и поперечной силы (трение).
Аналитическое решение задачи сводится к интегрированию из-вестного дифференциального уравнения продольно- оперечного изги-ба балки на упругом основании:
|
|
|
|
|
dx 2 dx 2 dx 2
Краевые условия в зависимости от особенности конструкции опоры и инженерно-геологических условий могут быть приняты в сле-дующем виде.
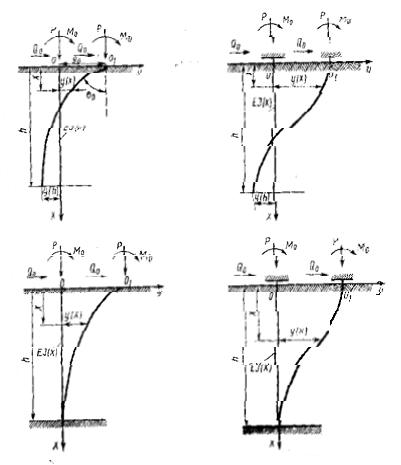
1. Опора со свободными концами (рис. 8, а): у (0) =y 0; y ¢(0) = q0;
|
2. Опора с жёстко закреплённым подвижным верхним и свобод-ным нижним концами (рис. 8, б):
|
|
3. Опора со свободным верхним и жёстко закреплённым нижним концом (свая–стойка) (рис. 8, в):
у (0) = y 0; y ¢(0) = q0;
|
4. Опора с жёстко закреплённым подвижным верхним и жёстко закреплённым неподвижным нижним концами (свая–стойка) (рис. 8, г):
y (0) = у 0; y (0) = q0= 0;
|
y (h) = y ¢(h) = 0.
а) б)
в) г)
Рис. 8. Расчётные схемы опор с различными раевыми условиями
Общее решение однородного уравнения, построенного методом последовательного приближения, согласно формуле, имеет вид:
yn (х) – у 0 А (х) + q0 B (x) + M 0(x) + М 0 С (х) + Q 0 D (х),
где А (х), В (х), С (х) и D (x) – функции.
В расчёте свай переменного сечения на совместные действия вер-тикальной и горизонтальных нагрузок методом конечных элементов свая рассматривается как гибкий стержень, заглублённый в много-слойное основание, характеризуемый коэффициентом постели С (х). Свая по длине мысленно разбивается на n онечных элементов.
Выделенный конечный элемент имеет четыре степени свободы – перемещения U 1и U 2, углы поворота 1и 2концов элемента в уз-лах. Функция прогибов элемента принята в виде кубического полино-ма. Коэффициенты при переменных определяются с учётом граничных условий на концах элемента.
Уравнения для перемещений записаны в матричной форме
|
|
|
|
|
|
|
Для определения матрицы жёсткости сваи, заглубленной в линей-но-деформируемое грунтовое основание, характеризуемое коэффици-ентом постели, использован принцип Лагранжа о минимуме потенци-альной энергии системы «сваи – грунт» в виде
|
|
|
Матрица жёсткости элемента K э состоит из матрицы жёстко-сти изгиба сваи K c и матрицы жёсткости отпора грунта K г.
K э= K c+ K г,
где
l
|
|
|
|
|
2
l
|
|
|
|
2
Коэффициент постели принят постоянным в пределах каждого конечного элемента.
|
|
|
|
|
В НИИ оснований под руководством В.Г. Федоровского исследо-вана НДС комбинированных плитно-свайных фундаментов (КПСФ). В таком фундаменте нагрузку воспринимает плита и сваи. Решена осе-симметричная задача теории упругости МКЭ. Конечные элементы для свай, грунта и плиты – прямоугольные, составленные из двух тре-угольных. Жёсткости контактных КЭ для контакта свай и плиты с грунтом, а также внутри грунта принимали по модулю деформации грунта, а на контакте плиты со свае<
|
|
|
