 |
Взаимодействие электромагнитных волн
|
|
|
|
С ВЕЩЕСТВОМ
Дисперсией света называется явлениезависимость показателя преломления вещества от длины волны (или частоты) падающего излучения.
Качественной характеристикой этого явления служит производная от показателя преломления по длине волны, называемая дисперсией вещества D:
d n
D = –––. (1.38)
d λ
При нормальной дисперсии показатель преломления вещества уменьшается с увеличением длины волны, и d n / d λ < 0. Это имеет место для всех прозрачных бесцветных материалов.
При аномальной дисперсии показатель преломления увеличивается с увеличением длины волны и d n / d λ > 0. Этот случай наблюдается вблизи полос поглощения света.
Согласно молекулярной теории дисперсии света вдали от областей поглощения света
 (1.39)
(1.39)
где ε – диэлектрическая постоянная вещества; ω 0 – собственная частота колебаний молекул; ω – частота падающего излучения; m и e – масса и заряд электрона.
Строго монохроматическая волна распространяется со скоростью
ω λ λ с
v = ω / k = -––- = ν λ = ––- = –––-, (1.40)
2π Т n
которая называется фазовой скоростью. Здесь λ – длина волны; k = 2π /λ –волновое число (измеряется в 1/м, м-1); Т - период колебаний; с – скорость волны в вакууме.
Пакет (группа) волн в диспергирующей среде распространяется с групповой скоростью
d ω
u = –––-. (1.41)
d k
Связь междуфазовой и групповой скоростями описывается формулой Рэлея
dvdv
u = v + k –––- = v - k –––-. (1.42)
d k d λ
Из этой формулы видно, что в зависимости от знака dv/d λ групповая скорость может быть как больше, так и меньше фазовой скорости. В недеспергирующей среде dv/dλ =0, и обе скорости совпадают.
ПРИМЕР. Показатели преломления дистиллированной воды для света длин волн λ1 = 486 нм и λ2 = 509 н соответственно равны n 1= 1,3371 и n 2 = 1, 3360. Определить средние значения фазовой и групповой скоростей в этом интервале длин волн.
|
|
|
РЕШЕНИЕ. Считая, что показатель преломления в заданном интервале длин волн изменяется линейно, среднюю фазовую скорость v определим как среднюю арифметическую скоростей v1 и v2, которые найдем из соотношений v1 = с / n 1 и v2= с / n 2, где с – скорость света в вакууме.
v1 + v2 с 1 1 3∙108 1 1
<v> = ––––––- = –– (–- + ––-) = –––– (–––––- + ––––––-) = 1,24∙108 м/с.
2 2 n 1 n 2 2 1,3371 1, 3360
При определении групповой скорости заменим производную dv/dλ приращениями Δv/Δλ, что вполне обоснованно при малых интервалах Δv и Δλ, как в нашей задаче. Тогда средняя групповая скорость будет равна
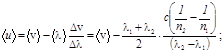

Отметим, что групповая скорость в данной задаче меньше фазовой, т.е. мы находимся в области нормальной дисперсии. Это следует и из условия задачи, поскольку показатель преломления воды уменьшается с увеличением длины волны.
При прохождении света через поглощающее вещество интенсивность света ослабляется по закону Бугера
 (1.43)
(1.43)
Здесь I0, I – интенсивности света на входе и выходе из поглощающего слоя толщиной d; k – коэффициент поглощения излучения (измеряется в 1/м, м-1); е – основание натурального логарифма, е = 2,72. Для растворов k = βс, где с – концентрация растворенного вещества; β – коэффициент поглощения на единицу концентрации вещества.
ПРИМЕР. Пучок монохроматического света поочередно пропускают через две пластинки толщиной d = 1 см. Коэффициент поглощения первой пластинки в 4 раза меньше коэффициента поглощения второй. Интенсивность света на выходе из второй пластинки в 3 раза меньше, чем из первой. Коэффициенты отражения света от поверхностей пластинок одинаковы. Определить коэффициенты поглощения k 1 и k 2 обеих пластинок.
|
|
|
РЕШЕНИЕ. Пусть интенсивность света, падающего на пластинки I0, коэффициент отражения света каждой пластинки r. Тогда из первой пластины выйдет свет интенсивности

из второй-

Учитывая, что k 2= 4 k 1, найдем отношение интенсивностей

Прологарифмируем правую и левую части последнего выражения:

Подставим числовые значения и определим k 1 и k 2:
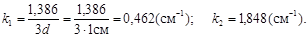
ФОТОНЫ
Согласно квантовой теории свет может испускаться и поглощаться только порциями (квантами). Энергия кванта света, или фотона определяется как
ε = hν = ћω = hc /λ, (1.44)
где h= 6,63∙10-34 Дж∙с, ћ = h /2π = 1,02∙10-34 Дж∙с – постоянные Планка; ν и ω – частоты и циклическая частоты излучения; – длина волны излучения; с = 3∙108 м/с – скорость света в вакууме.
Импульс фотона
р = mc = ε / c = hν / с = ћω/с =h / λ. (1.45)
При соударении с поверхностью фотоны передают ей импульс, вследствие чего возникает световое давление Р. При нормальном падении светового потока на поверхность с коэффициентом отражения давление света равно
Е е
Р = ––––(1 + ρ) или Р = ω (1 + ρ), (1.46)
с
где Е е = W / St = Nhν / St – облученность поверхности, т.е. энергия всех N фотонов, падающих в единицу времени на поверхность площадью S; – объемная плотность энергии излучения.
|
|
|


