 |
Условие однозадачности.
|
|
|
|
Оператор выходов:
Определение динамики выходных сигналов.
В отличие от оператора переходов H, который каждый момент времени t на интервале от 
до t из множества t ставит в соответствие определенный элемент 
, оператор G на каждом моменте времени t определяет выходной сигнал.
Оператор 
- оператор функционирования системы.
Совокупность точек 
, которое соответствует всем моментам времени 
, называется траекторией функционирования системы.
Стохастические системы без последствий.
Пусть 
- пространство элементов случайных событий, и для каждого случайного события 
определена вероятность 
, тогда:
= 
- Оператор переходов.
- Оператор выходов.
Если зафиксировать 
, то система будет называться системой со случайными начальными состояниями.
Если зафиксировать 
, то будет получена система со случайными переходами.
Если зафиксировать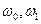 
, то будет получена система со случайными выходами.
Информационные системы отличаются большим числом элементов, которые могут иметь разный характер и разнообразное взаимодействие между элементами. Поэтому для описания ИС вводится понятие агрегата. Это унифицированная модель для описания функционирования разнородных элементов систем. Динамика ИС может быть записана с помощью сопряженных между собой агрегативных моделей элементов (см. пред. лекцию).
Агрегат характеризуется множеством моментов времени T, состоянием в каждый момент времени Z, входным сигналом 
и выходным сигналом 
.
Для агрегата рассматривается каждое состояние системы в момент времени t , так и в момент времени (t + 0) 
, в который агрегат может перейти за малый промежуток времени.
|
|
|
Вид оператора перехода H будет зависеть от того, поступил или нет входной сигнал в течение рассмотренного промежутка времени.
Пусть в момент времени 
в агрегат поступает входной сигнал 
, тогда состояние агрегата в момент времени + 0:
при 
.
Если за интервал времени 
в систему не поступило механических сигналов за исключением момента времени 
, то:
при 
Во множестве состояний Z можно выделить некое подмножество 
, что если составить 
будет достигнуто состояние , то момент t* будет являться моментом выдачи агрегатом выходного сигнала:
В некоторых случаях возможно изменение состояния системы в момент выдачи выходного сигнала, когда состояние 
выходит на границу .
Чтобы учесть этот факт, вводится 
, который все это учитывает:
Таким образом, совокупность операторов 
задает ранее описанные нами операторы переходов H, а совокупность операторов H и G полностью определяет модель функционирования агрегата.
Процесс функционирования агрегата состоит из скачковых состояний в момент поступления входного сигнала (
), и в момент выдачи выходного сигнала (), а также в момент изменения состояния агрегата между этими моментами (
).
Агрегативное описание системы и ее элементов достаточно универсально и подходит для различных математических моделей функционирования элементов и систем.
Для создания такой агрегатной модели функционирования ИС необходимо:
- Разработать агрегатные модели элементов.
- Построить модель сопряжения между элементами.
Агрегат может быть управляемым, а для того, чтобы рассмотреть управление агрегата, необходимо из множества входных сигналов выделить подмножество управляющих сигналов. С этом случае модель функционирования ИС зависит от принятых принципов управления. Рассмотрим основные классы структуры системы управления.
|
|
|
