 |
Закон сохранения импульса.
|
|
|
|
В §3 мы ввели понятие импульса материальной точки как величины, равной  . Импульс – аддитивная величина, то есть импульс системы материальных точек есть геометрическая сумма всех
. Импульс – аддитивная величина, то есть импульс системы материальных точек есть геометрическая сумма всех 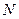 импульсов системы:
импульсов системы:
 .
.
Продифференцируем эту сумму по времени и учтем, что производная импульса есть сила:
 .
.
Здесь  и
и  – силы, действующие со стороны второй и третьей материальной точки на первую точку,
– силы, действующие со стороны второй и третьей материальной точки на первую точку,  и
и 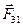 а – силы, действующие со стороны первой точки на вторую и третью. Вследствие Третьего закона Ньютона они попарно сокращаются. Также попарно сокращаются все внутренние силы, действующие в систем е материальных точек. Остается только
а – силы, действующие со стороны первой точки на вторую и третью. Вследствие Третьего закона Ньютона они попарно сокращаются. Также попарно сокращаются все внутренние силы, действующие в систем е материальных точек. Остается только  – результирующая или равнодействующая сил, действующих на систему материальных точек извне:
– результирующая или равнодействующая сил, действующих на систему материальных точек извне:
 .
.
Если же система замкнута, то  равна нулю и тогда после интегрирования производной полного импульса, находим
равна нулю и тогда после интегрирования производной полного импульса, находим
 .
.
Это математическая формулировка закона сохранения полного импульса замкнутой системы материальных точек. «Полный импульс замкнутой системы материальных точек не зависит от времени, то есть сохраняется».
Задачи, для решения которых применяется закон сохранения полного импульса, достаточно известны. В частности ранее утверждалось, что если на корме небольшой лодки поставить вентилятор, который будет дуть в парус, то лодка останется неподвижной. Это не всегда так и опыты подтверждают это. Так, если не весь поток воздуха будет попадать на парус, то часть импульса проходящего мимо паруса не будет компенсировать силу отдачи и лодка начнет двигаться кормой вперед. Похожий эффект возникает, если молекулы воздуха упруго отражаются от паруса. Тогда импульсы и силы перераспределяются в пространстве, что создает отличную от нуля внешнюю силу. Картина в целом напоминает случаи рассеяния света на поглощающей и отражающей поверхностях.
|
|
|
Теорема о движении центра масс.
Пусть есть система 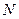 материальных точек с массами
материальных точек с массами  имеющими координаты
имеющими координаты  . Тогда точка с координатами
. Тогда точка с координатами 
 ,
,
где  называется полной массой системы, называется центром массы системы (иногда эту точку называют также центром инерции системы).
называется полной массой системы, называется центром массы системы (иногда эту точку называют также центром инерции системы).
Рассматривая центр масс системы, вводят специальную теорему о его движении. Мы введем эту теорему в рассмотрение, сделав несколько шагов.
1. Имеются внешние силы, действующие на каждую i-ю частицу,  , и внутренние силы действующие между частицами,
, и внутренние силы действующие между частицами,  .
.
2. Согласно Третьему закону Ньютона,  .
.
3. Согласно Второму закону Ньютона для i-й частицы,  .
.
4. Но  . Получаем ряд уравнений, соответствующих правым частям:
. Получаем ряд уравнений, соответствующих правым частям:
5. 
6. Сложим почленно указанные уравнения. Видно, что все внутренние силы попарно сокращаются. Остаются только внешние силы:
 .
.
Это Второй закон Ньютона для системы материальных точек.
7. Из определения центра масс следует
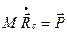 .
.
8. Продифференцировав по времени, находим,
 .
.
Теперь теорема: Центр массы системы движется как материальная точка массы М. на которую действует результирующая сила всех внешних сил. Если эта результирующая сила равна нулю, то полный импульс системы постоянен во времени.
Работа механической силы.
А). Работа постоянной силы при прямолинейном перемещении; сила и перемещение S совпадают по направлению. Согласно определению, работой в этом случае называется произведение  . Размерность работы, как и энергии, равна Дж (или Н).
. Размерность работы, как и энергии, равна Дж (или Н).
Б). Если вектор силы и вектор прямолинейного перемещения составляют угол  , то работа равна
, то работа равна  . Например,
. Например,  . Здесь
. Здесь  – обозначение скалярного произведения двух векторов.
– обозначение скалярного произведения двух векторов.
Случаи А) и В) рассмотрены для постоянной по величине и направлению силы.
В). Если же сила непостоянна по времени или направлению, то надо брать очень маленькие перемещения  , на протяжении которых сила не меняется. Тогда можно ввести понятие элементарной работы,
, на протяжении которых сила не меняется. Тогда можно ввести понятие элементарной работы,  , или, в более общем виде
, или, в более общем виде  ,
,  – элементарное (бесконечно малое) а значит – прямолинейное смещение.
– элементарное (бесконечно малое) а значит – прямолинейное смещение.
|
|
|
Г). Полная работа произвольной силы при перемещении по прямой L от начальной точки а до конечной точки в равна определенному интегралу
 .
.
Д). Не всегда перемещение происходит по прямой линии. В этом случае рассматривают кривую линию с начальной точкой а и конечной точкой в,  , и определенное интегрирование проводят по малым (прямолинейным) отрезкам этой кривой. Такой определенный интеграл называется криволинейным и обозначается как
, и определенное интегрирование проводят по малым (прямолинейным) отрезкам этой кривой. Такой определенный интеграл называется криволинейным и обозначается как
 .
.
Этот интеграл даёт наиболее общее выражение для работы произвольной силы.
Е). Есть еще один случай работы силы, который надо упомянуть. Это работа по замкнутой траектории. В этом случае обозначается кружком на знаке криволинейного интеграла:
 .
.
Здесь начало и конец кривой (траектории) совпадают и их не отмечают. Такие интегралы (мы их вычисляем для простейших случаев, когда вычисления очевидны и легки) крайне важны. Мы обсудим их значение позже, а пока отметим, что в том случае, когда
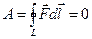 ,
,
сила называется консервативной, а работа равна нулю независимо от выбора замкнутого контура. Примерами служат сила упругости, сила тяжести, сила Кулона и др. Если же

 ,
,
то сила называется неконсервативной. Её работа зависит от вида траектории L. Это силы трения (сухого и вязкого) силы необратимых деформаций др.
С понятием «работа» связано понятие «мощность». Мощность – это работа, совершаемая в единицу времени или «скорость» совершения работы:
 .
.
Мощность Р – скаляр, не путать с модулем импульса.
Потенциальная энергия.
Как было отмечено, потенциальная энергия – это величина, показывающая, какую работу может совершить механическая система. Причем эта работа связана с массой и скоростью материальной точки. Другой тип механической энергии – это потенциальная энергия. Она менее универсальна, чем кинетическая энергия и проявляется не всегда. Одна из важных особенностей потенциальной энергии состоит в том, что она всегда определяется с точностью до произвольной постоянной. Работа, которую совершает система с потенциальной энергией, равна разности потенциальной энергии в начальном и конечном состояниях. Приведем несколько примеров.
|
|
|
Пусть материальная точка массой m находится на высоте h над горизонтальной поверхностью. Тогда говорят, что её потенциальная энергия равна  , где g – ускорение свободного падения при данных условиях. При этом мы могли бы проводить отсчет «высоты», скажем, от потолка комнаты. Независимо от этого и вне зависимости от вида траектории, по которой падает материальная точка (свободное падение, без трения), работа совершаемая силой тяжести одинакова и равна
, где g – ускорение свободного падения при данных условиях. При этом мы могли бы проводить отсчет «высоты», скажем, от потолка комнаты. Независимо от этого и вне зависимости от вида траектории, по которой падает материальная точка (свободное падение, без трения), работа совершаемая силой тяжести одинакова и равна  .
.
Подобным же образом потенциальной энергией обладает материальная точка на пружине, жесткость которой равна k. В самом деле, при небольших растяжениях пружины  , где
, где  – длина недеформированной пружины можно записать силу Гука
– длина недеформированной пружины можно записать силу Гука
 .
.
Если пружину растягивать (заметим, что перемещения конца пружины противоположно по направлению действующей силы, что приводит к замене знака «–» на знак «+»), то совершаемая над пружиной работа, равная запасенной потенциальной энергии, составит
 .
.
Полная потенциальная энергия определяется неопределенным интегралом, то есть равна
 .
.
Произвольная постоянная может быть задана, если указать начало системы отсчета. Если конец нерастянутой пружины совпадает с началом отсчета, то константу принимают за нуль.
Потенциальная энергия связана с силой, действующей на систему. Рассматривая движение только вдоль оси Х, легко установить, что
 ,
,
или, точнее,
 .
.
Обобщение последней формулы на трехмерное движение дает
 .
.
Выражения, стоящие справа (без учета знака «–») называют оператором набла,  , или оператором градиент,
, или оператором градиент,  , или просто записывают в виде
, или просто записывают в виде  . Все эти обозначения эквивалентны. Использование «круглых» символов
. Все эти обозначения эквивалентны. Использование «круглых» символов  и подобных им показывает, что производная вычисляется при фиксированных значениях остальных пространственных переменных, то есть вычисляется частная производная.
и подобных им показывает, что производная вычисляется при фиксированных значениях остальных пространственных переменных, то есть вычисляется частная производная.
|
|
|


