 |
Относительная погрешность приближенного значения точного числа
|
|
|
|
Точность измерения характеризуется с помощью относительной погрешности.
Относительной погрешностью  приближенного значения х называется отношение абсолютной погрешности этого значения к модулю точного значения а:
приближенного значения х называется отношение абсолютной погрешности этого значения к модулю точного значения а:
 Если точное значение а неизвестно, то используют предельную относительную погрешность — такое положительное число δ, что
Если точное значение а неизвестно, то используют предельную относительную погрешность — такое положительное число δ, что  .
.
Для вычисления относительных погрешностей часто используются приближенные формулы 
Эти формулы тем точнее, чем ближе значение х к точному значению а, т. е. чем меньше погрешность  или Δ.
или Δ.
Пример. Каковы предельные абсолютная и относительная погрешности числа 1.41 — приближенного значения числа  ? Так как 1,410 <
? Так как 1,410 <  < 1,415, то
< 1,415, то

Следовательно, можно положить Δ = 0.005. Далее,  , откуда δ = 0.0036 или δ = 0.36%.
, откуда δ = 0.0036 или δ = 0.36%.
Говорят, что приближенное значение х (записанное в виде десятичной дроби) имеет n верных знаков, если абсолютная погрешность этого числа меньше или равна половине единицы его n -го разряда.
Например, если 9.263 имеет три верных знака (9, 2 и 6), то абсолютная погрешность этого числа
 .
.
Элементарными функциями называются функции одного аргумента, значения которых получаются с помощью конечного числа вычислительных операций над аргументом, зависимой переменной и постоянными числами. Разложение элементарных функций в степенные ряды
Разложение  .
.
Лемма. Если для любого отрезка  при любом
при любом  , то
, то  .
.
Доказательство. Для произвольного  выберем
выберем  так, чтобы
так, чтобы  . Применим к
. Применим к  формулу Тейлора с остаточным членом в форме Лагранжа:
формулу Тейлора с остаточным членом в форме Лагранжа:  , где
, где  . По условию,
. По условию,  и
и  . По признаку Даламбера ряд с членами
. По признаку Даламбера ряд с членами  сходится (
сходится (  ). Поэтому его общий член
). Поэтому его общий член  стремится к 0, значит и
стремится к 0, значит и 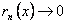 при
при 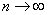 . Ввиду произвольности
. Ввиду произвольности  получаем, что
получаем, что  .
.
|
|
|
Для получения разложения  заметим, что
заметим, что  , и для любого отрезка
, и для любого отрезка 
 . Поэтому лемма применима с
. Поэтому лемма применима с  , и мы получаем:
, и мы получаем:  .
.
Для нахождения разложения 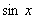 и
и  учтем, что
учтем, что 
 и в лемме можно положить
и в лемме можно положить  . Поэтому
. Поэтому 

Разложения для  позволяет нам вывести очень важные для дальнейшего формулы Эйлера. Сначала дадим необходимые определения.
позволяет нам вывести очень важные для дальнейшего формулы Эйлера. Сначала дадим необходимые определения.
Если члены ряда  - комплексные числа (
- комплексные числа ( 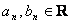 ), то сходимость ряда
), то сходимость ряда  означает, что одновременно сходятся ряды
означает, что одновременно сходятся ряды  и
и  . Абсолютная сходимость ряда
. Абсолютная сходимость ряда  , по определению, есть сходимость ряда
, по определению, есть сходимость ряда  , т.е. ряда
, т.е. ряда  .
.
Очевидные неравенства  показывают, что абсолютная сходимость ряда
показывают, что абсолютная сходимость ряда  равносильна одновременной абсолютной сходимости рядов
равносильна одновременной абсолютной сходимости рядов  ,
,  и абсолютно сходящиеся ряды с комплексными членами обладают всеми свойствами абсолютно сходящихся рядов с действительными членами.
и абсолютно сходящиеся ряды с комплексными членами обладают всеми свойствами абсолютно сходящихся рядов с действительными членами.
Подставим в разложение для  вместо
вместо  величину
величину  . Тогда (пока формально) получим:
. Тогда (пока формально) получим:  . Группируя действительные и мнимые слагаемые, получаем:
. Группируя действительные и мнимые слагаемые, получаем:  .
.
Для обоснования законности наших действий заметим, что ряд 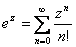 , как доказано выше, абсолютно сходится, поэтому в нем можно переставить слагаемые (в частности так, как это сделано выше), и сумма его сохранится. Упомянем, что и для
, как доказано выше, абсолютно сходится, поэтому в нем можно переставить слагаемые (в частности так, как это сделано выше), и сумма его сохранится. Упомянем, что и для  .
.
Если в разложение для  подставить вместо
подставить вместо  число
число 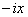 , то получим:
, то получим:  . Поэтому из двух полученных формул следует, что
. Поэтому из двух полученных формул следует, что 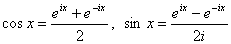 . Кроме того, для любого комплексного числа
. Кроме того, для любого комплексного числа  .
.
Разложение  .
.
Используем равенство: 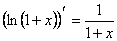 . Разложим
. Разложим  в ряд как прогрессию при
в ряд как прогрессию при 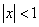 .
. 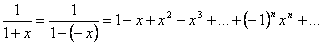 . Тогда, интегрируя это разложение, получим:
. Тогда, интегрируя это разложение, получим:  . Это равенство справедливо при
. Это равенство справедливо при 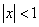 . Кроме того, т.к. ряд
. Кроме того, т.к. ряд  сходится по теореме Лейбница, равенство сохранится и при
сходится по теореме Лейбница, равенство сохранится и при  .
.
Разложение  .
.
Используем равенство:  . Далее, как и выше, при
. Далее, как и выше, при 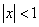
 . Поэтому, при
. Поэтому, при 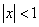
 . Кроме того, ряд
. Кроме того, ряд  сходится. Значит, написанное выше разложение имеет место и при
сходится. Значит, написанное выше разложение имеет место и при  .
.
Разложение  .
.
Если обозначить  , то
, то  . Поэтому
. Поэтому  . Это разложение верно для всех
. Это разложение верно для всех  , где
, где 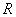 - радиус сходимости. Для нахождения
- радиус сходимости. Для нахождения 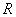 используем формулу
используем формулу  . Кроме того, без доказательства, отметим, что при
. Кроме того, без доказательства, отметим, что при  разложение справедливо и при
разложение справедливо и при  , а при
, а при  - для
- для  .
.
|
|
|
В заключение приведем несколько полезных следствий из разложения  .
.
Следствие 1. Легко видеть,  . Поэтому
. Поэтому  при
при 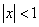 . Полагая
. Полагая  , получаем, что
, получаем, что  и
и  . Этим разложением можно воспользоваться при вычислении логарифмов и при доказательстве формулы Стирлинга.
. Этим разложением можно воспользоваться при вычислении логарифмов и при доказательстве формулы Стирлинга.
Следствие 2. Формула Стирлинга.
Приведем эту формулу без доказательства. 
9. Приближенное решение алгебраических уравнений
80. Интерполяция
Интерполя́ция, интерполи́рование — в вычислительной математике способ нахождения промежуточных значений величины по имеющемуся дискретному набору известных значений.
Многим из тех, кто сталкивается с научными и инженерными расчётами часто приходится оперировать наборами значений, полученных экспериментальным путём или методом случайной выборки. Как правило, на основании этих наборов требуется построить функцию, на которую могли бы с высокой точностью попадать другие получаемые значения. Такая задача называетсяаппроксимацией. Интерполяцией называют такую разновидность аппроксимации, при которой кривая построенной функции проходит точно через имеющиеся точки данных.
Существует также близкая к интерполяции задача, которая заключается в аппроксимации какой-либо сложной функции другой, более простой функцией. Если некоторая функция слишком сложна для производительных вычислений, можно попытаться вычислить её значение в нескольких точках, а по ним построить, то есть интерполировать, более простую функцию. Разумеется, использование упрощенной функции не позволяет получить такие же точные результаты, какие давала бы первоначальная функция. Но в некоторых классах задач достигнутый выигрыш в простоте и скорости вычислений может перевесить получаемую погрешность в результатах.
Следует также упомянуть и совершенно другую разновидность математической интерполяции, известную под названием «интерполяция операторов». К классическим работам по интерполяции операторов относятся теорема Рисса-Торина (Riesz-Thorin theorem) и теорема Марцинкевича (Marcinkiewicz theorem), являющиеся основой для множества других работ.
|
|
|
Определения
Рассмотрим систему несовпадающих точек  (
(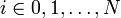 ) из некоторой области
) из некоторой области  . Пусть значения функции
. Пусть значения функции  известны только в этих точках:
известны только в этих точках:
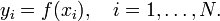
Задача интерполяции состоит в поиске такой функции 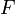 из заданного класса функций, что
из заданного класса функций, что

§ Точки  называют узлами интерполяции, а их совокупность — интерполяционной сеткой.
называют узлами интерполяции, а их совокупность — интерполяционной сеткой.
§ Пары  называют точками данных или базовыми точками.
называют точками данных или базовыми точками.
§ Разность между «соседними» значениями  — шагом интерполяционной сетки. Он может быть как переменным так и постоянным.
— шагом интерполяционной сетки. Он может быть как переменным так и постоянным.
§ Функцию  — интерполирующей функцией или интерполянтом.
— интерполирующей функцией или интерполянтом.
Пример
1. Пусть мы имеем табличную функцию, наподобие описанной ниже, которая для нескольких значений  определяет соответствующие значения
определяет соответствующие значения  :
:

| 
|
| 0,8415 | |
| 0,9093 | |
| 0,1411 | |
| −0,7568 | |
| −0,9589 | |
| −0,2794 |
Интерполяция помогает нам узнать какое значение может иметь такая функция в точке, отличной от указанных (например, при x = 2,5).
К настоящему времени существует множество различных способов интерполяции. Выбор наиболее подходящего алгоритма зависит от ответов на вопросы: как точен выбираемый метод, каковы затраты на его использование, насколько гладкой является интерполяционная функция, какого количества точек данных она требует и т. п.
2. Найти промежуточное значение (способом линейной интерполяции).
| 15.5 | |
| ? | |
| 19.2 |

|
|
|


