Экспериментальный поиск. Метод Гаусса-Зайделя.

Во-вторых, эксперимент почте всегда дороже, чем единичный расчет целевой функции. Расчетная задача, где приходится 1000 раз считать F, может оказаться не очень большой по объему. Эксперимент же по отыскиванию оптимума, требующий 100 опытов, – уже очень велик.

В-третьих, при экспериментальной оптимизации характер зависимости F от факторов, как правило, бывает проще, чем при расчетной. Это объясняется тем, что ошибки опытов «сглаживают рельеф» целевой функции. Таким образом, в эксперименте обычно можно работать с простейшими математическими моделями – чаще всего с многочленами 1-го или 2-го порядков.

При оптимизации методом Гаусса — Зейделя поиск оптимума исследуемого процесса осуществляется поочередным варьированием каждого входного параметра до дости­жения частного оптимума выходного параметра. Вначале достигает­ся оптимум по направлению одной из координатных осей при фик­сированных значениях входных параметров по другим координат­ным осям. Затем, зафиксировав найденное значение выходного параметра, переходят к варьированию другого входного параметра, где вновь достигается частное значение оптимума и т. д. На рис. 71 изображены линии равного выхода целевой функции при двух вход­ных параметрах (л^и х₂) и общие представления о действии метода Гаусса — Зейделя.

 

 

 

Рисунок – Поиск оптимума методом Гаусса-Зайделя

Это наиболее простой метод оптимизации, который широко ис­пользуется в практике исследований в химии и химической техно­логии. Следует, однако, отметить, что указанным способом редко попадают в область оптимума. Чаще всего ограничиваются одно­кратным варьированием по каждой из координатных осей (точка В, рис. 71), что главным образом связано с основным недостатком ме­тода — длительностью продвижения в область оптимума.

32. Симплекс - решетчатые планы Шеффе.

Из числа наиболее опробованных планов можно указать два типа симметричных планов: Шеффе и Дрейпера-Лоуренса. Первые для двух- и трехкомпонентных смесей при одинаковом числе параллельных наблюдений в каждой точке плана в случае моделей в виде третьей степени весьма удачны. Они минимизируют случайные ошибки предсказания этими моделями поверхности отклика. Однако точность моделей ухудшается при использовании планов Шеффе выше третьего порядка.

Планы на симплексных решетках, т.е. планы Шеффе, не обладают обычно свойством композиционности, т.е. для перехода к построению более сложной модели исследователю приходится ставить новые опыты, не полностью используя информацию, полученную из предыдущих опытов. Чтобы уменьшить подобные потери, либо выбирают координаты для контрольных точек в точках плана модели более высокого порядка, либо сразу строят план модели более высокого порядка (n₂>n₁). В многокомпонентных сплавах приходится строить полиномы сравнительно высоких степеней. Условие нормировки облегчает эту задачу, позволяет вместо полных многочленов вида

y=b₀+

использовать либо канонические полиномы Шеффе:

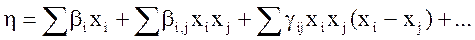
либо однородные полиномы:

Число экспериментальных точек симплексного плана зависят от числа компонентов изучаемой смеси к и выбранной степени полинома

,

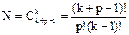где к – число компонентов в смеси, р – степень полинома

Например для получения модели четвертой степени (р =4) для системы из пяти компонентов (к =5) необходимо провести следующее число опытов (N)

Использование приведенных полиномов позволяетт уменьшить число опытов для аппроксимации свойств и оценки адекватности модели полиномами одного и того же порядка.

Виды моделей и расчет коэффициентов. Коэффициенты аппроксимирующих полиномов представляют собой комбинации значений изучаемого свойства, полученных в узлах симплексных решеток для S-компонентных смесей n-го порядка.

Например, в модели второго порядка для трехкомпонентной смеси:

 

Модель второго порядка для S-компонентной смеси:

 

 

Чтобы воспользоваться формулами вычисления коэффициентов моделей следует оговорить расположение экспериментальных точек, значения показателя в которых подставляются в эти формулы.

В каждой узловой точке симплекса третьего порядка содержится по три части компонентов.

В первой точке смесь состоит из трех частей третьего компонента; в шестой точке к одной части первого компонента добавлено две части второго; в восьмой – к двум частям второго добавлена одна часть третьего, а десятая точка содержит по одной части всех трех компонентов.

 

 

 

Рисунок 1 – Барицентрическая система Рисунок 2 – { S, n}-решетка

координат Шеффе { S, n} = {3, 3}

Чтобы ставить эксперимент на решетке трехкомпонентного симплекса четвертого порядка, следует иметь в виду, что смеси во всех узловых точках в этом случае состоят уже из четырех частей. Так, например, в четвертой точке содержится три части первого и одна часть третьего компонента и т. д.

⇐ Предыдущая10111213141516171819Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: