 |
Колебания линейной механической системы с одной степенью свободы около положения устойчивого равновесия
|
|
|
|
5.4.1. Свободные колебания. Рассмотрим консервативную систему с голономными и стационарными связями, имеющую одну степень свободы. В этом случае выражение для кинетической энергии имеет вид
, (5.9)
где всегда положительный обобщенный коэффициент инерции может зависеть от обобщенной координаты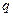 
.
Для получения линейной математической модели разложим 
в ряд Маклорена по степеням 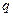и отбросим все слагаемые, начиная со второго порядка малости (т.е. рассмотрим только малые колебания около положения устойчивого равновесия).
Тогда 
и выражение (5.9) будет иметь вид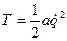 
.
Рассуждая аналогично, для потенциальной энергии можно получить выражение 
, где обобщенный коэффициент жесткости 
.
При таких колебаниях механической системы (линейной изначально либо линеаризованной, как это сделано нами выше) дифференциальное уравнение движения может быть получено, например, способом Лагранжа (4.4).
Тогда 
; (5.10.а)
либо 
; где 
. (5.10.б)
Дополняя это уравнение начальными условиями 
, будем иметь полную математическую модель для отыскания закона движения 
.
Виды решения этого дифференциального уравнения общеизвестны:
, (5.11)
здесь 
, либо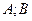 
, либо 
- постоянные интегрирования.
При заданных начальных условиях второй вид (5.11) будет
, (5.12)
для третьего вида амплитуда колебаний 
,
начальная фаза колебаний 
.
Как видно, величина 
имеет смысл частоты свободных колебаний (число колебаний за 
единиц времени); она связана с периодом 
этих колебаний соотношением 
.
ПРИМЕР 5.3. Воздушный взрыв дал кораблю начальную скорость в вертикальном направлении 
. Зная площадь его ватерлинии 
, водоизмещение 
и присоединенную массу жидкости в вертикальном направлении 
, найти для корабля период и амплитуду вертикальных колебаний. Развалом бортов и сопротивлением воды пренебречь.
|
|
|
РЕШЕНИЕ. Обозначим вертикальное перемещение корабля 
. Запишем дифференциальное уравнение вертикальных колебаний корабля, спроецировав на вертикаль силы, на него действующие (см.рис.5.4).
Тогда 
,
где 
- удельный вес воды.
Приведем уравнение к виду (5.10.б)
, здесь 
. 
Период вертикальных колебаний будет 
.
Запишем начальные условия: 
. Подставив их в (5.12), получим:
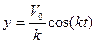, где 
.
5.4.2. Учет линейно – вязкого сопротивления. Силу, зависящую от скорости точки и противоположную ей по направлению, называют силой трения или сопротивления (демпфирования). Часто действующие на точки механической системы силы сопротивления 
можно считать прямо пропорциональными скоростям 
этих точек
. (5.13)
Здесь 
- коэффициент пропорциональности. Энергетической характеристикой всей совокупности этих сил (аналог (5.1), (5.2)) является диссипативная функция Рэлея (функция рассеивания энергии)
, (5.14)
где 
- обобщенные коэффициенты сопротивления.
Очевидно, что для системы с одной степенью свободы (5.14) примет вид
.
При известной функции Релея уравнения Лагранжа второго рода примут вид
; 
. (5.15)
Тогда для системы с одной степенью свободы получается следующая математическая модель
. (5.16)
При .
Здесь 
и 
.
Для действительных значений параметра 
, когда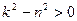 
(малое сопротивление), получается следующее решение:
. (5.17)
Иная форма записи, содержащая амплитуду 
и начальную фазу 
, имеет вид
; 
;
.
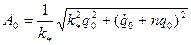Движение системы с линейным сопротивлением вообще не является периодическим и с течением времени затухает.
При малом трении локальные максимумы отклонений повторяются через равные интервалы времени 
(см. рис.5.5).
Удобной характеристикой затухания является логарифмический декремент, представляющий собой натуральный логарифм отношения любых двух последовательных локальных максимумов и 
:
|
|
|
.
Для критического значения демпфирования 
(или 
) решение уравнения (5.16) имеет вид
.
При больших значениях коэффициента сопротивления, когда 
, решение представляется в виде
; (5.18)
.
Здесь 
и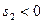 
, так что обобщенная координата постепенно убывает, как и при 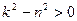(см.рис.5.6).
ПРИМЕР 5.4 (задача 32.62 из [5]). Для определения сопротивления воды движению модели судна при малых скоростях модель М пустили плавать в бассейн, прикрепив нос и корму посредством двух одинаковых пружин А и В, силы натяжения которых пропорциональны удлинениям (рис.5.7). 
Результаты наблюдений показали, что отклонения модели от положения равновесия после каждого размаха уменьшаются, составляя геометрическую прогрессию, знаменатель которой равен 0.9, а продолжительность каждого размаха постоянна и равна 
= 0.5сек. Определить силу сопротивления 
воды, приходящуюся на каждый килограмм массы модели, при скорости ее равной 1 м/сек.
РЕШЕНИЕ. Поскольку амплитуды размахов составляют геометрическую прогрессию, а продолжительности размахов одинаковы, сила сопротивления жидкости пропорциональна скорости движения, т.е. 
, где 
- масса модели в килограммах, а 
- скорость горизонтального движения модели в м/сек. Составим дифференциальное уравнение горизонтального движения модели
, где 
- суммарная жесткость пружин А и В.
Приведем уравнение к виду (5.15)
, где 
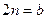, а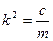 
.
Воспользуемся формулой, связывающей декремент затухания с продолжительностью размахов
.
Прологарифмируем полученное выражение и найдем
.
5.4.3. Вынужденные колебания под действием гармонической вынуждающей силы. Можно выделить два типа возбуждения вынужденных колебаний:
- колебания вызываются вынуждающими силами (силовое возбуждение); при этом его частным, но достаточно распространенным случаем является силовое гармоническое возбуждение 
;
- колебания вызываются заданным во времени перемещением (абсолютным или относительным) точки (или точек) механической системы (кинематическое возбуждение). Важным частным случаем такого возбуждения является гармоническое возбуждение 
.
На рисунке 5.8 для простейшей механической системы, состоящей из амортизированного груза, приведены различные типы возбуждения гармонических колебаний:
|
|
|
а - возбуждение силовое,
б – кинематическое, с заданным абсолютным смещением точки крепления пружины,
в - кинематическое, с заданным относительным смещением конца поршня демпфера,
г – кинематическое, с заданным относительным движением (вращением) несбалансированной части в виде математического маятника (инерционное возбуждение).
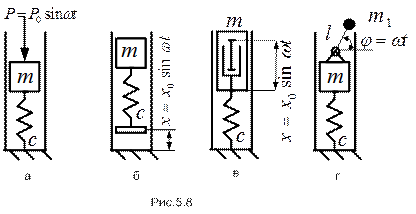
Независимо от типа возбуждения (силовое или кинематическое) при гармоническом воздействии уравнение Лагранжа приводится к виду
. (5.18)
Здесь 
- амплитуда возбуждения, которая может быть:
- постоянной – первый тип возбуждения (рис.5.8.а);
- пропорциональной частоте 
- второй тип возбуждения (рис.5.8.в);
- пропорциональной квадрату частоты - второй тип возбуждения (рис.5.8.б,г).
Решение уравнения (5.18) имеет вид
. (5.19)
Оно отличается от решения (5.11) наличием слагаемого
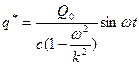(5.20)
которое в технике называется вибрацией. Очевидно, что вибрация представляет собой моногармонические колебания с частотой вынуждающего воздействия и амплитудой
.
Зависимость 
для первого типа возбуждения называется амплитудно-частотной характеристикой или динамической податливостью системы. Отнесенная к статической податливости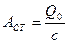 
эта величина называется коэффициентом динамичности 
.
Зависимость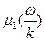 
, одинаковая для всех систем с одной степенью свободы, приведена на рис.5.9.а.
Она показывает, во сколько раз смещение от динамического воздействия на систему с частотой превышает статическое смещение, вызываемое силой (
). Отметим, что при 
вынуждающая сила и смещение сонаправлены, при 
– находятся в противофазе.
При 
(резонанс) установившихся колебаний нет, и в отличие от (5.20) решение имеет вид
,
т.е. колебания постепенно нарастают. В системах с сопротивлением (см. параграф 5.6) резонансный режим движения с конечной амплитудой существует.
Графики аналогов коэффициента динамичности для возбуждений второго типа (
- когда пропорциональна и 
, когда пропорциональна 
), приведены на рис.5.9.б и 5.9.в, соответственно.
Замечания: 1. При действии на линейную механическую систему полигармонического воздействия решение может быть получено в виде суммы решений, выполненных для каждого из гармонических воздействий.
|
|
|
2. При действии на линейную механическую систему воздействия, допускающего разложение в ряд Фурье, решение может быть получено как сумма решений для каждого из членов ряда. Очевидно, что такой подход удобен только в том случае, если ряд сходится достаточно быстро и для получения решения с удовлетворяющей нас точностью можно оставить сравнительно небольшое количество членов разложения.
3. При действии на линейную механическую систему произвольного воздействия можно воспользоваться, например, методом вариации произвольных постоянных, предложенного впервые Лагранжем. Его применение выходит за рамки пособия, но с ним можно ознакомиться, например, в [2].
5.4.4. Вынужденные колебания с демпфированием. В случае гармонического возбуждения при учете сил сопротивления дифференциальное уравнение имеет вид
(5.21)
при .
Полностью с учетом начальных условий колебательный процесс описывается системой соотношений
(5.22)
где - угол фазового отставания силы от смещения 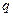, подчиняющийся условию
.
Из (5.22) видно, что при любых числах 
и 
, т.е. при любых начальных условиях, решение с течением времени приближается к виду
. (5.23)
Вводя, как в предыдущем параграфе, понятие коэффициента динамичности 
, получим для первого типа возбуждения (постоянная амплитуда вынуждающей силы) выражение
.
Для возбуждений второго типа соответствующие коэффициенты будут связаны прежними зависимостями:
; .
График зависимости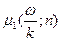 
приведен на рис.5.10.
Заметим, что с ростом сопротивления максимальные значения амплитуд вынужденных колебаний уменьшаются, а при 
в зоне резонанса максимальное значение вообще отсутствует. Хотя максимумы этих функций несколько смещены влево относительно резонансной частоты 
, такие смещения настолько малы, что принято считать максимальными (резонансными) значения 
Эту величину так же называют добротностью механической системы: чем она больше, тем больше резонансные амплитуды.
|
|
|
