 |
Действующий элемент и его связи. Стр. 2
|
|
|
|
Коэффициенты частичного эффекта дают нам в сумме матрицу с n строками и m столбцами. Обозначим эту матрицу через А и запишем так:
| (2.5) |
Эту матрицу будем называть матрицей трансформации. Как видно, она состоит из всех коэффициентов частичного эффекта действующего элемента.
С помощью матрицы трансформации правило преобразования входного вектора Х в выходной вектор У можно выразить в виде системы уравнений:
| (2.6) |
Это можно записать проще:
| (2.7) |
где 
- векторы (а именно 
) Как видим, правило преобразования, которое символизирует оператор Т, представлено здесь в виде алгебраических действий, которые образую эту трансформацию.
Выражение правила трансформации в виде представленных выше уравнений будем называть дифференциальным видом этого правила (Ланге, 1969).
Если коэффициенты частичного эффекта αij являются постоянными, то мы получаем интегральный вид правила преобразования:
| (2.8) |
или проще:
| Y=A · X | (2.9) |
В правую часть полученных уравнений могут быть добавлены и произвольные постоянные величины. Для простоты будем полагать, что они равны нулю.
Дифференциальный вид указывает на отношение между изменениями вектора Х и изменениями вектора У, интегральный вид правила трансформации указывает на отношения между значениями вектора Х и вектора У.
В случае, когда коэффициенты частичного эффекта αij являются постоянными и интегральное преобразование имеет вид записанных выше уравнений, мы будем говорить, что трансформация является линейной.
Если коэффициенты частичного эффекта αij не являются постоянными величинами, то они будут функциями вектора Х. В этом случае матрица трансформации А является функциональной матрицей.
|
|
|
Действующий элемент и его связи. Стр. 3
Если вектор Х - это непрерывная величина, то полученные нами ранее уравнения будут являться дифференциальными. Их решение (если, конечно, оно существует) состоит из системы функций:
| (2.10) |
Эту систему также можно в общем виде записать проще:
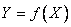
| (2.11) |
Трансформация вектора Х в вектор У позволяет определить состояние выходов нашего действующего элемента на основании данных о состоянии его входов. Иногда возможна и обратная трансформация, которую мы будем обозначать так:
| (2.12) |
Обратная трансформация позволяет на основании анализа состояния выходов действующего элемента делать некоторое заключение о состоянии его входов.
Обратная трансформация сводится к решению полученных векторных уравнений относительно вектора Х при данном конкретном значении выходного вектора У. Как известно из курса алгебры, обратная трансформация возможна при выполнении двух условий.
1. Во-первых, должно быть n m. Это условие необходимо потому, что иначе уравнений было бы меньше, чем неизвестных (которыми являются составляющие вектора Х, а их число равно m). Иными словами, диверсификация элемента не может быть отрицательной, поскольку в таком случае количество выходов элемента не было бы достаточным для определения состояния его входов.
2. Во-вторых, ранг матрицы трансформации должен быть равным m, иначе говоря, ровно m частичных эффектов изменения состояния отдельных входов должны быть линейно независимыми.
Если обратная трансформация возможна, то правило преобразования для линейной трансформации можно записать в следующем виде:
| (2.13) |
Здесь А-1 является матрицей, обратной относительно матрицы А.
Обратной называют матрицу А-1, которая, будучи умножена на матрицу А, в результате дает единичную матрицу I, где:
|
|
|
|
